Почвенная эрозия представляет собой процесс разрушения почвогрунтов под воздействием следующих основных факторов: ветра и водных потоков. Процесс эрозии причиняет большой вред народному хозяйству, например потеря сельскохозяйственных угодий оценивается приблизительно в 2 млрд гектаров, включая около 50 млн гектаров пахотных земель.
Исследования в области изучения эрозионных процессов начались еще с середины прошлого столетия и продолжаются до сих пор, так как актуальности эрозия не потеряла: ежегодно обширные площади сельхозугодий, склонов, да попросту отвалов земли подвергаются размыву, выходя из строя.
Большой вклад в разработку способов оценки противоэрозионной стойкости почв внесли В.Б. Гуссак, Г.И. Швебс, Г.В. Бастраков, М.С. Кузнецов. В эмпирических моделях деструкции почвы широкое распространение получили относительная оценка противоэрозионной устойчивости Иванова В.Д. и Сурмача Г.П. В основном практически все методы дают аналогичные оценки смываемости основных типов почв по зонам [1; 2].
Сложность и трудоемкость измерения количества грунта, подвергающегося эрозии, в полевых условиях предопределили интенсивное развитие исследований в области математического моделирования эрозионных процессов. Первоначально исследователи, не имея достаточного экспериментального материала, в основном брали за основу по большей части элементарные представления о гидравлике склоновых потоков [3; 4].
Среди российских эмпирических моделей эрозионного процесса наиболее популярна разработка В.Д. Иванова, Г.П. Сурмача и Государственного гидрологического института (ГГИ) [5; 6]. Модель ГГИ построена на весьма обширном экспериментальном материале и учитывает зависимость смыва от слоя стока. Испытание этой модели показывает, что разработанные учеными методы имеют неточности, а именно завышают количество грунта, который переходит в склоновый сток, а модель ГГИ занижает данный показатель. Главным дефектом модели ГГИ считается то, что она не учитывает дину склона, а этот факт приводит к тому, что исключается вероятность применения ее для проектирования мер по предотвращению эрозионных процессов. Кроме того, в модели использовано слишком огрубленное деление почв по противоэрозионной стойкости, а применяемый слой весеннего половодья ликвидирует вероятность учета воздействия физико-химической структуры почвогрунта на динамику склонового стока.
В модели эрозионных процессов, предложенной Г.И. Швебсом [7], предусмотрено воздействие энергии ливня на способность склонов противостоять размывающему действию струй, и предложен механизм, описывающий динамику склонового стока. Недостатком данной модели является то, что данные о зависимости смыва от водоотдачи, определяемые эмпирически по воздействию водного потока на малые площади, скорость которого близка к максимуму, привели к неточности в сторону завышения воздействия интенсивности водоотдачи на смыв.
Ранее мы предложили кинетическую модель описания эрозионных процессов, в основе которой лежат постулаты формальной химической кинетики [8]. Основной эмпирической константой предложенного уравнения является масса грунта, переходящая в склоновый сток в единицу времени. Существенным недостатком предложенной модели является трудоемкость определения массы смываемого грунта в полевых условиях.
В настоящей работе нами предпринята попытка исследовать динамику склонового стока в зависимости от высоты слоя почвогрунта, перешедшего в склоновый сток в рассматриваемом поперечном сечении, и оптимизировать предложенное нами ранее дифференциальное уравнение для описания эрозионных процессов [8].
Цель исследования: оптимизация кинетической модели, описывающей процесс поверхностной эрозии.
Материалы и методы исследования
Процесс эрозии моделировали, используя лабораторную дождевальную установку типа ЛДУ-1М [9]. Исследовались почвогрунты, взятые в бассейне реки Десна Трубчевского района.
Зависимость динамики склонового стока от высоты склона в рассматриваемом сечении изучали, используя следующую методику. Грунт предварительно увлажняли до наименьшей влагоемкости, которая показывает количество воды, удерживаемое почвой в практически неподвижном состоянии после обильного полива и стекания гравитационной влаги. Затем формировали искусственный откос для моделирования ливневых осадков на склон.
Исследовали частный случай, когда воздействие водного потока на поверхность отвала грунта происходит таким образом, что объем влаги, размывающий грунт, оказывает воздействие на склон выше первого расчетного створа, а затем устремляется вниз, проходя через расчетные сечения. В данном случае моделируется процесс, происходящий, например, при снеготаянии, когда на склон воздействует поток воды с вышележащей водосборной площади. Измеряли высоту слоя почвогрунта, перешедшего в склоновый сток в контрольном сечении в определенных временных интервалах.
Обработка экспериментальных результатов проводилась с помощью математического моделирования с применением компьютерного программного пакета – Mathcad, по известной методике [10].
Результаты исследования и их обсуждение
Как было показано нами ранее [8], кинетическая модель эрозионных процессов склонового стока должна учитывать анализ механизма рассматриваемого процесса и составление его схемы, которая отражает переход исходного грунта в склоновый сток.
Схема смыва грунта приведена на рис. 1.
На рассматриваемой схеме представлены следующие элементы:
I–I – верхняя граница склона;
II–II – рассматриваемое вертикальное сечение (расчетный створ);
III–III – нижняя граница склона;
1 – кривые пересечения поверхностей смыва в пространстве с вертикальной плоскостью сечения толщи грунта;
W – высота слоя почвогрунта, находящегося в естественном состоянии в рассматриваемом сечении, см;
Z – высота слоя почвогрунта, перешедшего в склоновый сток в сечении II–II, мм;
Wm – эрозионный потенциал, см/л;
Z0 – высота склона в рассматриваемом сечении, см;
l – расстояние от рассматриваемого сечения II–II до верхней границы склона I–I, см;
L – расстояние от сечения II–II до точки пересечения кривых «1» в разные временные интервалы, см;
0–0 – максимальная мощность слоя грунтов, вовлеченного в эрозионный процесс, см.
Для выражения процесса по схеме:
W + Z0 > Z + Wm (1)
используем уравнение, описывающее процесс взаимодействия двух компонентов системы
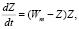 (2)
(2)
где m – комплексный параметр, характеризующий влияние комплекса различного характера факторов на склоновый сток.
Увеличение склонового стока будет равно уменьшению зоны не подвергшегося смыву в результате эрозии грунта, то есть
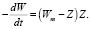 (3)
(3)
Таким образом, уравнения (2) и (3) описывают процесс взаимодействия двух компонентов системы «W» и «Z».
Интегрируя уравнение (2) при начальных значениях t = 0 и Z = Z0, получаем:
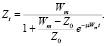 (4)
(4)
Кинетические кривые могут быть преобразованы в прямую линию, представлением результатов в координатах:
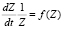
или
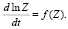 (5)
(5)
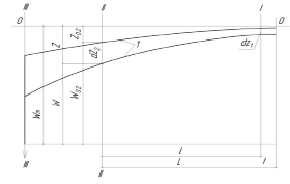
Рис. 1. Схема смыва грунта
Эмпирические константы μ(Wm), которые не изменяются во времени, для данного участка можно определить графически, продифференцировав кинетическую кривую, отражающую изменения толщи неэродированного грунта во времени.
При этом средняя скорость изменения склонового стока будет описываться уравнением:
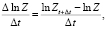 (6)
(6)
где Zt, Zt+Δt – склоновый сток к моментам времени t и Δt.
Подставим в уравнение (6) выражение Zt и Zt+Δt из уравнения (4):
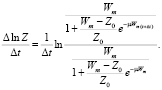 (7)
(7)
Из уравнения (4) выразим 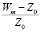 через Z:
через Z:
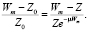 (8)
(8)
Преобразуя уравнение (7) относительно (8), получаем:
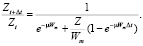 (9)
(9)
При представлении экспериментальных данных в координатах 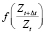 по оси абсцисс отсекается отрезок, равный высоте слоя почвогрунта, перешедшего в склоновый сток в конце временного периода (ZCT), а на оси ординат – отрезок
по оси абсцисс отсекается отрезок, равный высоте слоя почвогрунта, перешедшего в склоновый сток в конце временного периода (ZCT), а на оси ординат – отрезок 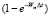 . Отсюда, зная величину Δt, можно найти значение параметра μWm. При этом необходимо, чтобы интервал времени между измерениями запасов склонового стока был одинаковым на протяжении всего периода измерений.
. Отсюда, зная величину Δt, можно найти значение параметра μWm. При этом необходимо, чтобы интервал времени между измерениями запасов склонового стока был одинаковым на протяжении всего периода измерений.
Проверку достоверности предлагаемой методики описания эрозионных процессов осуществляли, моделируя частный случай, когда воздействие на поверхность отвала почвогрунта происходит таким образом, что объем влаги, размывающий почвогрунт, действует на склон выше первого расчетного створа, а затем устремляется вниз, проходя через расчетные сечения. В данном случае моделируется процесс, происходящий, например, при снеготаянии, когда на склон воздействует поток воды с вышележащей водосборной площади.
Для проведения экспериментальных исследований были использованы почвогрунты, характерные для верхнего горизонта дерново-подзолистой почвы как одной из распространенных типов почв Трубчевского района Брянской области.
В качестве метода измерений был выбран метод учета эрозии по замеру высоты слоя почвогрунта, перешедшего в склоновый сток в контрольном сечении, так как с его помощью возможно без сложного оборудования на любом участке поля в первом приближении определять смыв почвогрунта от выпадения одного или нескольких ливней.
Процесс размыва почвогрунта и образование отрицательных форм рельефа заметен уже в первом сечении. При переходе вниз по склону наблюдается тенденция увеличения размыва почвогрунта, глубина борозд растет как в глубину, так и в ширину. В последнем расчетном створе наблюдается чёткое слияние отдельных борозд в единый поток.
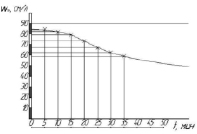
Экспериментальные данные размыва поверхности почвогрунта через одинаковые промежутки времени, равные пяти минутам, наносили на график. Примеры определения параметров Z, Wm, μWm по экспериментальным данным приведены на рис. 2.
Полное время протекания эрозионного процесса можно установить, используя уравнение:
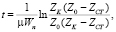 (10)
(10)
где ZK – высота слоя почвогрунта, перешедшего в склоновый сток в конце временного периода, мм;
ZСТ – высота слоя почвогрунта, перешедшего в склоновый сток в стационарном периоде процесса, мм.
Модель смыва грунта в процессе эрозии имеет вид:
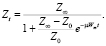 (11)
(11)
 а)
а) 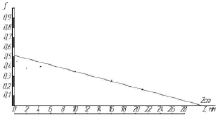 б)
б)
Рис. 2. а) кривая динамики эрозионного процесса в расчетном створе, б) линеаризованная кривая эрозионного процесса в расчетном створе
Выводы
1. Исследованы закономерности динамики склонового стока в зависимости от высоты склона в рассматриваемом поперечном сечении.
2. Оптимизирована кинетическая модель описания эрозионного процесса грунта, предложено дифференциальное уравнение, в котором основной определяемой константой является высота склона.
3. Полученные значения в результате теоретических расчетов хорошо согласуются с экспериментальными данными, что позволяет рекомендовать оптимизированную кинетическую модель для прогнозирования эрозионных процессов.
Библиографическая ссылка
Мельникова Е.А., Лукашов С.В., Иванченкова О.А., Левкина Г.В. СОВЕРШЕНСТВОВАНИЕ МЕТОДОВ МОДЕЛИРОВАНИЯ ПОЧВЕННО-ЭРОЗИОННЫХ ПРОЦЕССОВ НА ОСНОВЕ КИНЕТИЧЕСКОЙ МОДЕЛИ СКЛОНОВОГО СТОКА // Успехи современного естествознания. 2020. № 4. С. 120-124;URL: https://natural-sciences.ru/ru/article/view?id=37372 (дата обращения: 14.02.2026).
DOI: https://doi.org/10.17513/use.37372



