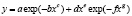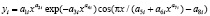За рубежом экспериментально исследуется динамика земель во взаимосвязи с другими видами деятельности человека. Например, в [1] дан подход к моделированию динамики земного покрова в зависимости от технологий землепользования. Выявлены связи между социально-экономической динамикой и изменениями в лесном покрове. Этот подход может быть использован для прогнозирования лесного покрова.
Корреляционный анализ между землепользованием и земельным покровом проведен [2] в муниципальном районе Абуджа (Нигерия) по данным дистанционного зондирования и обработки ГИС по трем космическим снимкам (1986, 2001 и 2016). Было обнаружено, что площадь застройки увеличилась на 246,96 км2 (86,4 %). Также обнаружено, что температура поверхности земли увеличилась в среднем с 23,5 до 30,2 °C. Сильная корреляция между классами земли и температурой наблюдалась на уровне 0.8266, 0.9486 и 0.7700 для трех измерений. Крупные районы были основными факторами изменений в муниципалитете Абуджа. Для обеспечения теплового комфорта необходима посадка деревьев – вот одна из рекомендаций.
В статье [3] показана связь между классификацией форм рельефа и растительностью на юго-западе провинции Фарс (Иран). Высокая корреляция 0.909 была получена для прогноза высоты деревьев с использованием классификации рельефа. С интенсификацией землепользования возрастает сброс сточных вод, что угрожает качеству поверхностных вод. Виды землепользования представляют разную степень опасности для водных ресурсов [4].
Для сопоставления долей земельных категорий с параметрами климата, рельефа, деревьев, количеством сточных вод и другими факторами вначале необходимо выяснить динамику коэффициента динамичности поведения специалистов в ходе землеустройства.
Цель исследования – методом идентификации [5] выявить закономерности изменения за период в 50 лет, с 1970 до 2020 г., коэффициента динамичности доли распределения земель по категориям кадастра на примере Волжского района Республики Марий Эл (РМЭ).
Из отчетов о распределении земельного фонда Волжского района Республики Марий Эл были выписаны данные (табл. 1) по доле семи категорий кадастра.
Таблица 1
Динамика доли земель Волжского района, %
|
Год |
Время, τ лет |
Доля площади земель по категориям |
||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
||
|
1970 |
0 |
51.55 |
3.11 |
1.19 |
- |
41.29 |
- |
2.86 |
|
1971 |
1 |
53.05 |
3.11 |
1.31 |
- |
41.26 |
- |
2.86 |
|
… |
… |
… |
… |
… |
… |
… |
… |
… |
|
2018 |
48 |
45.45 |
3.72 |
1.21 |
19.15 |
27.25 |
2.82 |
0.39 |
|
2019 |
49 |
45.45 |
3.72 |
1.21 |
19.15 |
27.25 |
2.82 |
0.39 |
|
2020 |
50 |
45.45 |
3.72 |
1.21 |
19.15 |
27.25 |
2.82 |
0.39 |
j = 1 – сельхозназначения (СХН); 2 – населенных пунктов; 3 – промышленности …; 4 – особо охраняемых территорий … (ООПТ); 5 – лесного фонда; 6 – водного фонда; 7 – запаса. С 1992 г. были выделены категории земельного кадастра 4 и 5.
Доли даны по простой формуле:
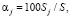 (1)
(1)
где α – доля, %, j – код, Sj – площадь j категории, S – общая площадь.
Коэффициент динамичности K вычисляется (табл. 2) по формуле
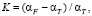 (2)
(2)
где αF – фактическое значение доли площади по категории (табл. 1), га; αT – расчетное по тренду значение доли площади, га. Чем больше K, тем динамичнее распределение.
Тренд динамики за 50 лет был выявлен по двухчленной формуле вида
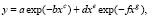 (3)
(3)
где y – зависимый показатель, x – влияющая переменная, a – g – параметры модели (3), идентифицируемые в программной среде CurveExpert-1.40 по данным табл. 2.
Таблица 2
Коэффициент динамичности доли земель Волжского района РМЭ
|
Год |
Время, τ лет |
Коэффициент динамичности доли площади по категориям |
||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
||
|
1970 |
0 |
-0.0015 |
0.0083 |
-0.1302 |
- |
-0.0031 |
- |
-0.0120 |
|
1971 |
1 |
-0.0061 |
0.0050 |
-0.0400 |
- |
-0.0039 |
- |
-0.0120 |
|
… |
… |
… |
… |
… |
… |
… |
… |
… |
|
1992 |
22 |
0.0808 |
- |
-0.1900 |
0.0017 |
-0.2786 |
0.0071 |
-0.9734 |
|
… |
… |
… |
… |
… |
… |
… |
… |
… |
|
2018 |
48 |
0.0028 |
-0.0017 |
0.0178 |
0.0000 |
-0.2731 |
-0.0015 |
2.4014 |
|
2019 |
49 |
-0.0044 |
-0.0038 |
0.0209 |
0.0005 |
-0.2821 |
-0.0016 |
3.1827 |
|
2020 |
50 |
-0.0117 |
-0.0059 |
0.0240 |
0.0010 |
-0.2898 |
-0.0016 |
4.1887 |
Идентификация тренда (3) менее трудоемкий процесс в сравнении с волновой функцией. К тому же тренд нужно будет выявить только один раз, так как не требуется идентифицировать асимметричный вейвлет множество раз. Наши исследования показали, что колебания можно определить по категориям земель до погрешности измерений. Поэтому в землеустройстве наблюдается почти полная квантовая определенность разложения динамических рядов на сумму асимметричных вейвлетов. Этот факт еще раз доказывает, что разделение территории на категории является изобретением человека, а не самой природной среды.
По модулю максимумы коэффициента динамичности наблюдаются: 1 категория – 0.0859 в 1996 г.; 2 – 0.0259 в 1978; 3 – 0.2171 в 1998; 4 – 0.0048 в 1998; 5 – 0.2898 в 2020; 6 – 0.0158 в 1998; 7 категория – 4.1887 в 2020 г. Наибольшую динамичность имеют доли земель запаса. При этом очень малую динамичность получают земли особо охраняемых природных территорий.
Тренды динамики долей категорий. Параметр общей площади исключается (табл. 3), что позволяет дополнять к долям семи категорий кадастра другие показатели.
Таблица 3
Параметры (3) динамики доли площади по категориям земель Волжского района
|
Код категории |
Тренд |
Коэф. корр. r |
||||||
|
Экспоненциальный закон |
Биотехнический закон [3] |
|||||||
|
a |
b |
c |
d |
e |
f |
g |
||
|
1 |
51.47273 |
-0.032345 |
0.70408 |
-0.43605 |
1.15916 |
0 |
0 |
0.8986 |
|
2 |
3.08455 |
-0.00067961 |
1.28251 |
0.0087425 |
1.48093 |
0.10832 |
0.76742 |
0.9898 |
|
3 |
1.36811 |
0.0025367 |
1.03693 |
8.68802e-8 |
9.23649 |
0.44301 |
1.10285 |
0.9280 |
|
4 |
18.27637 |
0.00062077 |
0.99902 |
0.016715 |
1.52302 |
0.030420 |
1.00024 |
0.8835 |
|
5 |
41.42000 |
5.14420e-6 |
2.85262 |
-6.58250e-13 |
12.93446 |
0.42329 |
1.00769 |
0.9668 |
|
6 |
2.82501 |
0 |
0 |
-2.88053 |
0 |
0.00034091 |
2.52720 |
0.8868 |
|
7 |
2.89474 |
2.77216e-7 |
3.01334 |
-1.58695e-26 |
23.07846 |
0.086521 |
1.58504 |
0.9757 |
Категории земель № 4 и 6 были введены в России только с 1992 года. В итоге эти две категории в табл. 3 также получили меньшие коэффициенты корреляции 0,8835 и 0,8868. Все тренды по табл. 3 получили уровень адекватности больше 0,7 или сильную связь.
Динамичность доказывается тем, что дополнительно к тренду получено еще множество колебаний, которые, как правило, являются конечномерными асимметричными вейвлетами. Выявление колебаний продолжается почти до ошибки измерений. Тогда можно утверждать, что площади и их доли по категориям земель относятся к вполне определяемым квантам поведения. В связи с этим коэффициент динамичности позволяет по тренду вычислять по формуле (2), и это облегчает процесс анализа динамики земель по категориям.
Из рис. 1 исключена категория ООПТ с малым коэффициентом динамичности.
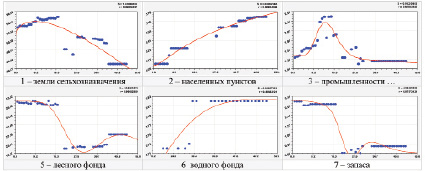
Рис. 1. Тренды динамики долей категорий земельного фонда Волжского района РМЭ с 1970 по 2020 г. (в правом верхнем углу: S – стандартное отклонение; r – коэффициент корреляции)
Вейвлеты коэффициента динамичности. Параметры всех вейвлетов даны в табл. 4.
Таблица 4
Параметры (4) коэффициента динамичности (1) долей площади земель Волжского района
|
Код категории |
Но- мер i |
Вейвлет |
Коэф. корр. r |
|||||||
|
Амплитуда (половина) колебания |
Полупериод колебания |
Сдвиг |
||||||||
|
a1i |
a2i |
a3i |
a4i |
a5i |
a6i |
a7i |
a8i |
|||
|
1 |
1 |
7.63146e-11 |
9.69680 |
0.48223 |
0.95573 |
10.58764 |
0.23095 |
0.22766 |
0.77238 |
0.9424 |
|
2 |
0.00023654 |
1.62395 |
0.00057009 |
2.08964 |
3.97256 |
0.011516 |
1.08961 |
-1.702310 |
||
|
3 |
1.97547e-6 |
3.50977 |
0.11165 |
0.98760 |
1.88124 |
0.011247 |
1.00134 |
0.28354 |
0.5608 |
|
|
4 |
9.16728e-14 |
9.33418 |
0.12226 |
1.14793 |
1.36393 |
0.0043571 |
0.98655 |
-1.41396 |
0.3585 |
|
|
2 |
1 |
0.00073338 |
3.82902 |
0.56652 |
0.98352 |
3.45877 |
0.020769 |
1.47778 |
0.91843 |
0.8149 |
|
3 |
1 |
-0.073940 |
0.38457 |
0.055856 |
1 |
5.49613 |
-4.89605e-7 |
2.13534 |
-0.21550 |
0.6954 |
|
2 |
0.00027297 |
3.25269 |
0.27795 |
0.89179 |
2.18825 |
0.13399 |
0.59726 |
1.21603 |
||
|
3 |
-1.15322e-6 |
6.25622 |
0.41003 |
0.95484 |
2.02225 |
-0.00045409 |
1.69047 |
-1.76800 |
0.6891 |
|
|
4 |
1.36004e-9 |
7.32618 |
0.18410 |
1.08419 |
5.90606 |
0.073925 |
0.92917 |
4.65873 |
0.4568 |
|
|
5 |
0.0030526 |
1.54799 |
0.010051 |
1.69995 |
0.63147 |
0.049435 |
0.68026 |
3.18144 |
0.6712 |
|
|
6 |
-0.13018 |
0 |
2.79430 |
1 |
1.00020 |
0 |
0 |
-0.01067 |
0.6722 |
|
|
7 |
-5.09532e-74 |
59.01923 |
0.015553 |
2.26974 |
11.29117 |
-0.0031889 |
2.23211 |
-2.10862 |
0.6667 |
|
|
8 |
-0.0026239 |
1.66650 |
0.28045 |
0.80062 |
2.74885 |
0.32567 |
1.17231 |
0.26601 |
0.4101 |
|
|
4 |
1 |
0.00022875 |
2.49031 |
0.20110 |
1.00122 |
5.12809 |
0.017479 |
1.04278 |
-2.35496 |
0.7664 |
|
5 |
1 |
1.87292e-7 |
4.45628 |
0.00060479 |
1.00196 |
0.84956 |
0.17579 |
0.98975 |
0.57140 |
0.9770 |
|
2 |
1.00411e-25 |
26.09208 |
1.11252 |
1.00065 |
0.46620 |
0.052211 |
1.01140 |
1.36445 |
||
|
3 |
-2.68743e-24 |
18.66028 |
0.32626 |
1.08290 |
6.01892 |
-0.00082751 |
1.60426 |
2.51011 |
0.6887 |
|
|
4 |
9.52462e-12 |
11.08623 |
0.52355 |
1.01320 |
1.08195 |
0.026019 |
1.00200 |
0.42307 |
0.6180 |
|
|
5 |
-0.0074176 |
1.14414 |
0.12430 |
1.00111 |
38.90826 |
0.10919 |
1.05278 |
-3.29726 |
0.5181 |
|
|
6 |
1 |
0.0038156 |
3.15096 |
0.33045 |
1.00665 |
6.49030 |
-0.0036896 |
1.31218 |
-2.17480 |
0.8899 |
|
2 |
0.00017752 |
3.33750 |
0.23724 |
1.01060 |
3.33170 |
-0.0082527 |
1 |
-0.041081 |
||
|
7 |
1 |
2.24084e-26 |
15.47109 |
0 |
0 |
0 |
0 |
0 |
0 |
0.8586 |
|
2 |
-6.72509e-45 |
43.21524 |
0.76385 |
1.20150 |
6.92857 |
0 |
0 |
-1.28537 |
||
|
3 |
8.22656e-75 |
66.27260 |
0.83103 |
1.22618 |
1.66825 |
-0.0094641 |
0.91045 |
-0.37831 |
0.9315 |
|
|
4 |
4.14588e-33 |
27.42522 |
0.49802 |
1.09078 |
0.68028 |
0.039600 |
1.05288 |
0.41559 |
0.5369 |
|
|
5 |
8.02904e-34 |
37.67122 |
3.09083 |
0.83569 |
0.16161 |
0.021506 |
0.96236 |
1.61731 |
0.8508 |
|
Изменение во времени коэффициента динамичности имеет волновую природу (табл. 4), и поэтому асимметричные колебания (вейвлет-сигналы) записываются волновой формулой [5] вида
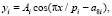
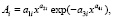
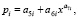 (4)
(4)
где y – зависимый фактор, i – номер составляющей, m – количество членов, x – объясняющая переменная, a1...a8 – параметры, получаемые в программной среде CurveExpert-1.40, Ai – амплитуда (половина) вейвлета (ось y), pi – полупериод колебания (ось x).
Динамический коэффициент получил по одному колебанию у доли земель населенных пунктов и особо охраняемых территорий. Два колебания характеризуют поведение доли водного фонда, четыре вейвлета у доли СХН, по пять колебаний у долей земель лесного фонда и земель запаса. Наибольшее количество колебаний (8 шт.) есть у земель промышленности.
Коэффициент динамичности доли земель СХН. Динамичность доли первой категории кадастра оказалась всего с четырьмя членами, при 18 членах по площади (рис. 2).
Остатки (рис. 2) показывают возможность выявления колебаний с малой амплитудой.
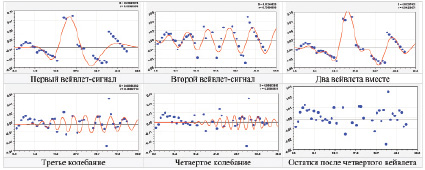
Рис. 2. Коэффициент динамичности распределения доли СХН Волжского района РМЭ (в правом верхнем углу: S – стандартное отклонение; r – коэффициент корреляции)
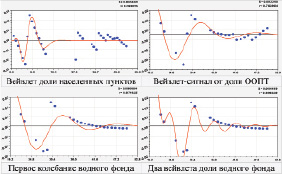
Рис. 3. Динамичность доли земель трех категорий Волжского района РМЭ
Динамичность доли земель населенных пунктов, ООПТ и водного фонда (рис. 3).
Сильные колебательные возмущения, как правило, были в последней четверти ХХ столетия. Остатки от вейвлета для населенных пунктов дают возможность выявления колебаний после 2000 г. А остатки от коэффициента динамичности доли ООПТ показывают значимость колебаний до 2000 г. Водный фонд в последние 20 лет также успокаивается по динамичности. Этот факт указывает на две возможные причины: 1) действительно земельный фонд Волжского района получил колебательную адаптацию; 2) землеустроители успокоились и стали ежегодно записывать одни и те же значения площади.
Динамичность доли земель промышленности …. Все графики даны на рис. 4.
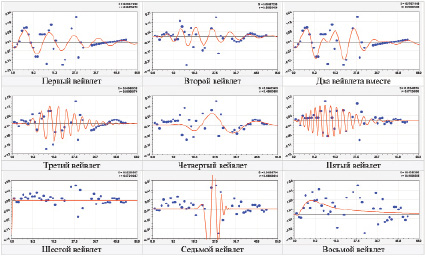
Рис. 4. Коэффициент динамичности доли земель промышленности Волжского района РМЭ
Вейвлеты № 1, 3, 6-8 получили отрицательный знак, и он указывает на кризис в росте коэффициента динамичности для земель третьей категории земельного кадастра. При этом можно сделать предположение, что периоды колебаний в 1970 г. зависели от циклов солнечной активности. Например, колебания № 1 и 4 почти совпадают со средним циклом солнечной активности в 11,3 года. С этим циклом также совпадает вейвлет № 7. Шестой вейвлет является откликом прошлого, то есть наблюдается влияние колебаний до 1970 г.
Коэффициент динамичности третьей категории земель имеет сильные колебания из-за планирования на территории Волжского района, кроме расширения Марийского бумажного комбината, еще ряда других деревообрабатывающих предприятий. Однако марийские леса сильно истощились по хвойным породам, а опыт Финляндии по применению лиственных пород в производстве бумаги так и не был использован. В итоге к настоящему времени произошел сильнейший спад в развитии промышленности Волжского района.
Динамичность доли земель лесного фонда. Первое колебание показывает, что слишком сильное колебательное давление оказывалось на леса Волжского района (рис. 5) с 1982 года. На это повлияло планирование города Волжска в советское время как крупного центра глубокой механической и химической технологий переработки древесины.
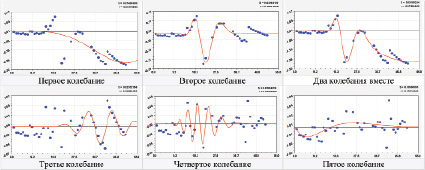
Рис. 5. Коэффициент динамичности доли земель лесного фонда Волжского района РМЭ

Рис. 6. Коэффициент динамичности доли земель запаса Волжского района РМЭ
Первые два вейвлета совместно дают самый высокий коэффициент корреляции 0,9770. Лесная политика была неустойчивой по второму колебанию с 1982 по 2007 год. Наиболее продолжительным был кризис по пятому колебанию с периодом в 1970 г. около 79 лет. В будущем колебания исключаются, и первое колебание показывает снижение амплитуды.
Коэффициент динамичности доли земель запаса. Эта категория показывает резкий рост коэффициента динамичности в будущем по закону степенной функции (рис. 6).
По абсолютной площади земли запаса в последние годы получили постоянное значение. Однако тренд на рис. 1 показывает снижение доли запаса. Поэтому на рис. 6 появляется новый тренд коэффициента динамичности в виде степенной функции. Тогда получается, что мониторинг земель фактически каждый год не актуализируется. Аналогично переписываются значения площади и по другим категориям земельного кадастра. Заметно также, что колебательные возмущения остались в прошлом. Поэтому актуальной становится задача повышения точности (снижения погрешности) измерений площади земель по семи категориям кадастра. Это позволит повысить точность вычисления долей в общей площади и снижения коэффициентов динамичности как площади, так и долей по категориям земельного кадастра.
Заключение
Коэффициент динамичности доли категорий за 50 лет показывает, что относительная доля площади категорий земельного кадастра дает более достоверную картину динамики поведения землеустроителей в сравнении с измерением площади.
Для анализа динамики категорий земельного кадастра, а затем последующего территориального планирования и прогнозирования в Российской Федерации срочно необходимы массивы официальных табличных данных площади и долей площади по всем муниципалитетам страны, причем не менее чем за 50 лет, с 1970 года.
На примере Волжского района РМЭ видно, что переход на доли категорий земельного кадастра дает более достоверную картину изменений коэффициента динамичности.
Идентификация тренда является менее трудоемкой в сравнении с волновой функцией. Тренд у каждой категории нужно будет выявить один раз. Наши исследования показали, что колебания можно определить по категориям земель до погрешности измерений. Поэтому в землеустройстве наблюдается почти полная квантовая определенность разложения динамических рядов на сумму асимметричных вейвлетов. Этот факт доказывает, что разделение территории на категории кадастра является изобретением человека, а не самой природной среды.
Коэффициент динамичности показывает, что при условии повышения точности измерений ежегодно должны быть разные значения площади по категориям земельного кадастра.
Исследование выполнено при финансовой поддержке Российского фонда фундаментальных исследований, Правительства Красноярского края, Красноярского краевого фонда науки в рамках научного проекта: «19-45-240004р_а Прогноз эколого-экономического потенциала возможных «климатических» миграций в Ангаро-Енисейском макрорегионе в меняющемся климате 21 века».
Библиографическая ссылка
Мазуркин П.М., Ефимова Е.А. КОЭФФИЦИЕНТ ДИНАМИЧНОСТИ ЗА 50 ЛЕТ ДОЛИ КАТЕГОРИЙ ЗЕМЕЛЬ // Успехи современного естествознания. 2021. № 6. С. 88-94;URL: https://natural-sciences.ru/ru/article/view?id=37646 (дата обращения: 17.02.2026).
DOI: https://doi.org/10.17513/use.37646