Города вносят основной вклад в изменение климата. По данным ООН Хабитат, города потребляют 78 % мировой энергии и производят более 60 % выбросов парниковых газов. Однако они занимают менее 2 % поверхности Земли (Cities and Pollution | United Nations).
В городах следует применять долгосрочный системный подход к адаптации к изменению климата и смягчению его последствий [1]. Силы были вызваны развитием и манипулированием окружающей средой в индустриальную эпоху. Последствия урбанизации и изменения климата сочетаются опасно, угрожая оказать беспрецедентное негативное воздействие на качество жизни, экономическую и социальную стабильность [2].
Оценки показывают, что города производят 75 % глобальных выбросов CO2, причем транспорт и здания являются одними из самых значимых источников [3]. Города растут, и по мере того, как происходит изменение климата, городской ландшафт будет продолжать ощущать последствия экологического кризиса [4]. Форма и планировка городов влияют на погоду и качество воздуха. Благодаря эффекту городского теплового острова города часто выглядят довольно благоуханными по сравнению с окружающей средой. На самом деле в городах бывает так жарко, что они начинают влиять на погоду и качество воздуха. Но все сводится не только к теплу, которое выделяют города, но и к их форме и расположению [5].
Цель исследования – выявление закономерностей [6] между 11 параметрами координат и высоты географического положения центров столиц, а также климата за 1960–1990 гг. и погоды за 2018 г. на территории 14 субъектов федерации Урала и Сибири.
Материалы и методы исследования
Составлены данные относительно геодезических координат и высоты положения центров столиц субъектов Федерации (три параметра), а также четырех факторов климата за период 1960–1990 гг. и четырех параметров погоды за 2018 г.
В табл. 1 дан фрагмент консолидированных данных по 14 субъектам из Уральского и Сибирского федеральных округов из сайта https://rosstat.gov.ru/accounts (дата обращения 07.08.2020), в частности из Российского статистического ежегодника, 2019. Данные по координатам столиц субъектов Федерации и их климату были взяты из источников Координаты в городах России, n.d. и Среднемесячные климатические данные, n.d.
Таблица 1
Фрагмент исходных данных по 40 параметрам
|
Код |
Субъект федерации Западной Сибири |
Столица субъекта |
Координаты |
||||
|
Х01 |
Х02 |
Х03 |
… |
Х40 |
|||
|
45 |
Курганская область |
Курган |
5,45 |
5,3333 |
75 |
… |
262,2 |
|
66 |
Свердловская область |
Екатеринбург |
6,8519 |
0,6122 |
255 |
… |
251,9 |
|
72 |
Тюменская область |
Тюмень |
7,1522 |
5,5272 |
81 |
… |
174,1 |
|
74 |
Челябинская область |
Челябинск |
5,154 |
1,4291 |
218 |
… |
251,0 |
|
4 |
Республика Алтай |
Горно-Алтайск |
1,9606 |
25,9189 |
285 |
… |
222,3 |
|
17 |
Республика Тыва |
Кызыл |
1,7147 |
34,4534 |
624 |
… |
378,1 |
|
19 |
Республика Хакасия |
Абакан |
3,7156 |
31,4292 |
247 |
… |
249,9 |
|
22 |
Алтайский край |
Барнаул |
3,3606 |
23,7636 |
189 |
… |
260,1 |
|
24 |
Красноярский край |
Красноярск |
6,0184 |
32,8672 |
139 |
… |
262,1 |
|
38 |
Иркутская область |
Иркутск |
2,2978 |
44,296 |
427 |
… |
320,1 |
|
42 |
Кемеровская обл. – Кузбасс |
Кемерово |
5,3333 |
26,0833 |
104 |
… |
342,8 |
|
54 |
Новосибирская область |
Новосибирск |
5,0415 |
22,9346 |
164 |
… |
232,1 |
|
55 |
Омская область |
Омск |
4,9924 |
13,3686 |
90 |
… |
220,3 |
|
70 |
Томская область |
Томск |
6,4977 |
24,9744 |
117 |
… |
201,3 |
Примечание: Выделены субъекты федерации Ангаро-Енисейского макрорегиона.
Для выявления закономерностей влияния трех географических параметров на 11 параметров трех групп (географические, климат и погода) были приняты условные обозначения:
1) географические координаты и высота положения центров столиц субъектов федерации (Х01 – приведенная северная широта, причем 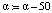 , 0; Х02 – приведенная восточная долгота, причем
, 0; Х02 – приведенная восточная долгота, причем 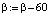 , 0; Х03 – высота над уровнем Балтийского моря, м);
, 0; Х03 – высота над уровнем Балтийского моря, м);
2) климатические среднемесячные па- раметры за 30-летний период 1961–1990 гг. (Х04 – средняя ночная температура, 0С; Х05 – средняя дневная температура, 0С; Х06 – средняя сумма осадков, мм; Х07 – среднее число дней с осадками >0,1 мм, шт.);
3) параметры погоды (2018) (Х08 – средняя температура, январь, 0С; Х09 – средняя температура, июль, 0С; Х10 – сумма осадков за январь, мм; Х11 – сумма осадков за июль, мм).
Результаты исследования и их обсуждение
Результаты идентификации данных из табл. 1 ранговых распределений (выделены курсивом) и пар с 11 фактором приведены в табл. 2.
Коэффициент коррелятивной вариации (по Ч. Дарвину коррелятивная вариация) по табл. 2 равен 19,7649 / (3 x 11) = 0,5989, и он дает средний (коэффициент корреляции от 0,5 до 0,7) уровень адекватности системы факторов. Сравнение объектов происходит по силе функциональной связности между всеми учтенными параметрами.
Таблица 2
Корреляционная матрица по трендам и рейтинг факторов
|
x |
Группа I |
Группа II |
Группа III |
Сумма Σrx |
Место Ix |
||||||||
|
Х01 |
Х02 |
Х03 |
Х04 |
Х05 |
Х06 |
Х07 |
Х08 |
Х09 |
Х10 |
Х11 |
|||
|
Х01 |
0,9954 |
0,6373 |
0,8674 |
0,5952 |
0,2242 |
0,5427 |
0,3521 |
0,7115 |
0,4510 |
0,4491 |
0,8208 |
6,6467 |
2 |
|
Х02 |
0,6526 |
0,9755 |
0,7402 |
0,8340 |
0,5937 |
0,2432 |
0,4314 |
0,7632 |
0,7382 |
0,4892 |
0,5587 |
7,0199 |
1 |
|
Х03 |
0,7646 |
0,5024 |
0,9913 |
0,4826 |
0,2428 |
0,5240 |
0,5545 |
0,7113 |
0,2965 |
0,2825 |
0,7458 |
6,0983 |
3 |
|
2,4126 |
2,1152 |
2,5989 |
1,9118 |
1,0607 |
1,3099 |
1,338 |
2,186 |
1,4857 |
1,2208 |
2,1253 |
19,7649 |
– |
|
|
2 |
5 |
1 |
6 |
11 |
9 |
8 |
3 |
7 |
10 |
4 |
– |
0,5989 |
|
Даны два рейтинга: 1) как влияющие переменные на первом месте находится Х02 – приведенная восточная долгота, на втором – приведенная северная широта и на третьем Х03 – высота над уровнем моря; 2) как зависимые показатели (критерии оценки) на первом месте расположился фактор Х03 – высота над уровнем Балтийского моря, на втором Х02 – приведенная восточная долгота и на третьем Х08 – средняя температура за 30 лет в январе.
Ранговые распределения трех параметров I группы показывают добротность измерений (табл. 3). Дополнительно к тренду были идентифицированы три колебания (вейвлета).
Рейтинг географических параметров дан по убыванию коэффициента корреляции:
1) 1,0000 Х03 – высота над уровнем Балтийского моря (рис. 1);
2) 0,9988 Х02 – приведенная восточная долгота (рис. 2);
3) 0,9974 Х01 – приведенная северная широта (рис. 3).

Рис. 3. Графики рангового распределения приведенной северной широты
Из-за введения вейвлетов малые изменения коэффициента корреляции (по вычислительным возможностям программной среды CurveExpert-1,40) не изменили места в табл. 2.
Таблица 3
Параметры вейвлетов рангового распределения географического положения
|
Но- мер i |
Вейвлет |
Коэф, корр, r |
|||||||
|
Амплитуда (половина) колебания |
Полупериод колебания |
Сдвиг |
|||||||
|
a1i |
a2i |
a3i |
a4i |
a5i |
a6i |
a7i |
a8i |
||
|
1,0000 Х03 – высота над уровнем Балтийского моря |
|||||||||
|
1 |
74,88229 |
0 |
–0,083913 |
1,20576 |
0 |
0 |
0 |
0 |
1/0000 |
|
2 |
–1,09956 |
0 |
–0,19132 |
1,27095 |
108,1762 |
–82,5505 |
0,087843 |
–1,24733 |
|
|
3 |
4,29896e6 |
14,05188 |
21,92848 |
0,32859 |
2,42095 |
–0,017978 |
1,49980 |
2,15369 |
0,9407 |
|
4 |
11,88306 |
8,94444 |
2,65029 |
1 |
1,01539 |
–0,0019601 |
1 |
4,61096 |
0,9281 |
|
5 |
3,47988 |
0 |
2,22844 |
1 |
4,09031 |
0 |
0 |
–1,43614 |
0,8106 |
|
0,9988 Х02 – приведенная восточная долгота |
|||||||||
|
1 |
4,34465e–21 |
0 |
–3,77755 |
1 |
0 |
0 |
0 |
0 |
0,9988 |
|
2 |
8,74845 |
3,18925 |
2,10578 |
0,45827 |
0 |
0 |
0 |
0 |
|
|
3 |
–1,46959 |
1,76679 |
0,35743 |
1 |
0,87987 |
0,12537 |
1 |
1,23892 |
|
|
4 |
0,00043509 |
4,99330 |
0,0030079 |
3,09054 |
0,98692 |
0,00054931 |
2,34460 |
–2,65407 |
0,9667 |
|
5 |
0,66132 |
0 |
1,91336 |
1 |
2,06069 |
0 |
0 |
0,40501 |
0,9985 |
|
0,9974 Х01 – приведенная северная широта |
|||||||||
|
1 |
1,71905 |
0 |
–0,056607 |
1,10874 |
0 |
0 |
0 |
0 |
0,9974 |
|
2 |
1,87826 |
3,93313 |
2,94508 |
0,46620 |
0 |
0 |
0 |
0 |
|
|
3 |
0,00027984 |
24,86442 |
10,07419 |
0,67599 |
92,1210 |
0 |
0 |
–1,35516 |
|
|
4 |
–0,19595 |
0,57786 |
0,010323 |
2,38088 |
0,89411 |
0,0017838 |
2,07207 |
1,72504 |
0,9995 |
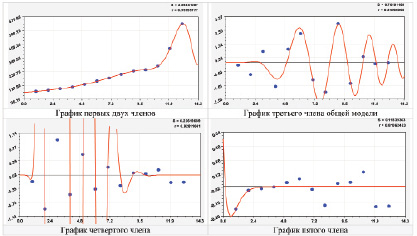
Рис. 1. Графики рангового распределения высоты над уровнем Балтийского моря (в правом верхнем углу: S – стандартное отклонение; r – коэффициент корреляции)
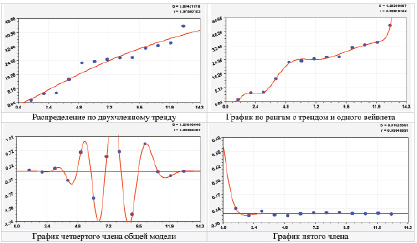
Рис. 2. Графики рангового распределения приведенной восточной долготы
Тренд с коэффициентом корреляции 0,9913 дает максимальную относительную погрешность |Δmax| = 35,77 %. Это Курган, столица Курганской области. При этом погрешность более 5 %, поэтому дальше моделировать нужно асимметричными вейвлетами (табл. 3). После пятого члена максимальная относительная погрешность стала |Δmax| = 0,08 %. Это уже относится к Челябинску. Модель по параметрам из табл. 3 является высокоадекватной.
На рис. 2 даны графики распределения по рангам при введенной восточной долготе.
После двухчленного тренда максимальная относительная погрешность равна |Δmax| = 204,39 % для восточной долготы, что значительно превышает допустимый уровень в 5 %. С тремя членами модели максимальная относительная погрешность снижается до 100,00 %. Это долгота Екатеринбурга. При этом всего две точки из 14 больше 5 %. Окончательно после пятого члена получилось |Δmax| = 0,72 % для Екатеринбурга.
На рис. 3 показаны графики рангового распределения приведенной северной широты для 14 субъектов федерации Западной Сибири.
Максимальная относительная погрешность тренда |Δmax| = 8,33 %. Это Абакан, столица Хакасии. По минимальной погрешности трендов северная широта занимает первое место, на втором – высота и на третьем – восточная долгота. Погрешность более 5 % у северной широты всего 2 точки из 14. После последнего, четвертого, члена модели максимальная относительная погрешность равна всего |Δmax| = 0,25 %. Это Кызыл, столица Республики Тыва.
Таким образом, применение к тренду дополнительно нескольких вейвлетов значительно снижает максимальную относительную погрешность моделей распределения.
Тогда получается, что рельеф по географическим параметрам имеет четкую волновую природу. Он получается из-за колебательной адаптации процессов горообразования и эрозии во времени геодинамики. Люди, основавшие города, выбирали на местности точки для установления центров по четким правилам, обусловленным многовековым опытом: прежде всего учитывались водный транспорт, защита от неприятелей, плодородная почва недалеко от городской стены.
В итоге центры городов, хотя за многие века и перемещались, являются хорошим примером сочетания параметров ландшафта и организации жизни в городах и территориях вокруг.
Парные отношения из-за малости количества субъектов и объема статьи моделируются только трендом. Выберем из табл. 2 сильные бинарные отношения с коэффициентом корреляции не менее 0,7 (табл. 4). Из общего количества бинарных отношений 3 х 11 – 3 = 30 шт. сильные факторные связи равны 10 шт., или по доле равно 33,33 % (третья часть).
Таблица 4
Корреляционная матрица парных отношений по трендам (1) при r ≥ 0.7
|
x |
Группа I |
Группа II |
Группа III |
||||||||
|
Х01 |
Х02 |
Х03 |
Х04 |
Х05 |
Х06 |
Х07 |
Х08 |
Х09 |
Х10 |
Х11 |
|
|
Х01 |
0,8674 |
0,7115 |
0,8208 |
||||||||
|
Х02 |
0,7402 |
0,8340 |
0,7632 |
0,7382 |
|||||||
|
Х03 |
0,7646 |
0,7113 |
0,7458 |
||||||||
Рейтинг сильных пар следующий (табл. 5): 1) 0,8674 Х01 → Х03; 2) 0,8340 Х02 → Х04; 3) 0,8208 Х01 → Х11; 4) 0,7646 Х03 → Х01; 5) 0,7632 Х02 → Х08; 6) 0,7458 Х03 → Х11; 7) 0,7402 Х02 → Х03; 8) 0,7382 Х02 → Х09; 9) 0,7115 Х01 → Х08; 10) 0,7113 Х03 → Х08.
В табл. 5 по убыванию коэффициента корреляции даны параметры всех отобранных 10 закономерностей по тренду из табл. 4. При условии c = 1 из первого члена тренда образуется закон Мандельброта (в физике), Лапласа (в математике), Ципфа–Перла (в биологии) и Парето (в эконометрике). При условии c ≠ 1 получается модифицированный нами закон Мандельброта. Дополнительно при условиях f = 0 и g = 0 вместо биотехнического закона образуется степенная функция. Отрицательный знак перед второй составляющей тренда показывает кризисное изменение показателя при влиянии Х01, Х02 или Х03.
Таблица 5
Параметры тренда бинарных отношений при r ≥ 0.7
|
Пере-менная x |
Пока- затель y |
Двухчленный тренд |
Коэф, корр, r |
||||||
|
Экспоненциальный закон |
Биотехнический закон |
||||||||
|
a |
b |
c |
d |
e |
f |
g |
|||
|
Х01 |
Х03 |
6918,4576 |
0,21987 |
0,85806 |
–7588,9455 |
0,36409 |
0,51655 |
0,70463 |
0,8674 |
|
Х02 |
Х04 |
–27,88048 |
–0,017132 |
1 |
–7,9943e–152 |
147,5549 |
4,99528 |
1 |
0,8340 |
|
Х01 |
Х11 |
126,33416 |
0,048289 |
1,48617 |
–0,23949 |
18,94809 |
5,29786 |
0,99731 |
0,8208 |
|
Х03 |
Х01 |
6,56639 |
0,0011818 |
1 |
–1,63282e–11 |
4,68214 |
0,00051370 |
1,39812 |
0,7646 |
|
Х02 |
Х08 |
–8,04891 |
–0,0096242 |
1 |
–8,52207 |
0,10697 |
0 |
0 |
0,7632 |
|
Х03 |
Х11 |
67,22798 |
7,23374e–5 |
1,89888 |
6,33050e–5 |
2,75455 |
0,0064646 |
0,97084 |
0,7458 |
|
Х02 |
Х03 |
282,94532 |
0,19940 |
1 |
1,24254e–6 |
7,04685 |
0,15805 |
1 |
0,7402 |
|
Х02 |
Х09 |
18,32800 |
–0,033824 |
1 |
–0,11711 |
1,67626 |
0 |
0 |
0,7382 |
|
Х01 |
Х08 |
–321,30800 |
0,28673 |
0,94760 |
375,45468 |
0,54865 |
0,69163 |
0,83092 |
0,7115 |
|
Х03 |
Х08 |
–21,15921 |
0,00025567 |
1 |
–1,11347e–9 |
3,58506 |
0 |
0 |
0,7113 |
На рис. 4 приведен график Х01 → Х03, который показывает зависимость изменения высоты положения центра столицы субъекта федерации Западной Сибири от влияния северной широты.
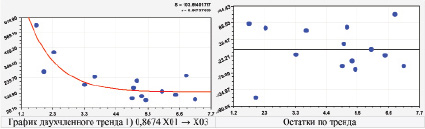
Рис. 4. Графики влияния северной широты на высоту положения столиц

Рис. 5. Графики моделей сильных влияний географических параметров на климат и погоду
Остальные парные отношения графически показаны на рис. 5.
Остатки на рис. 4 показывают возможность идентификации парных отношений дополнительно к тренду волновыми уравнениями. Однако известно, что для получения добротных вейвлетов необходимо принять количество субъектов не менее 20. Тогда придется рассматривать все субъекты федерации Сибири и Дальнего Востока совместно.
По рис. 5 пара Х02 → Х04 находится на втором месте. Тогда из графика видно, что в интервале приведенной долготы от 240 до 350 имеется снижение средней ночной температуры за 1960–1990 гг. Аналогичное изменение суммы осадков за июль происходит в интервале приведенной широты от 1,50 до 2,50 (широты от 51,50 до 52,50), Так анализируются все пары.
Заключение
Выявлены закономерности влияния координат и высоты географического положения центров столиц у 14 субъектов федерации Урала и Сибири на самих себя (по рангам), а также на параметры климата за 1960–1990 гг. и погоды за 2018 г.
Коэффициент коррелятивной вариации равен 0,5989, и он дает средний уровень адекватности матрицы из 3 х 11 факторов. Получены два рейтинга: 1) влияющей переменной: на первом месте Х02 – восточная долгота, на втором – северная широта и на третьем Х03 – высота над уровнем моря; 2) зависимым показателем: на первом месте Х03 – высота над уровнем моря, на втором Х02 – долгота и на третьем Х08 – средняя температура за 30 лет в январе.
Влияние рангов на высоту по пяти членам дает максимальную относительную погрешность 0,08 %. Это относится к Челябинску. Для долготы пятый член дал 0,72 % для Екатеринбурга. Модели широты по рангам дала 0,25 %. Это Кызыл, столица Республики Тыва. Пара Х01 → Х03 с корреляцией 0,8674 показывает изменение высоты от влияния широты. Пара Х02 → Х04 находится на втором месте. Видно, что в интервале приведенной долготы от 240 до 350 имеется снижение средней ночной температуры за 1960–1990 гг. Аналогичное изменение суммы осадков за июль происходит в интервале приведенной широты от 1,50 до 2,50 (широты от 51,50 до 52,50).
Исследование выполнено при финансовой поддержке Российского фонда фундаментальных исследований, Правительства Красноярского края, Красноярского краевого фонда науки в рамках научного проекта: «19-45-240004р_а Прогноз эколого-экономического потенциала возможных «климатических» миграций в Ангаро-Енисейском макрорегионе в меняющемся климате XXI века».
Библиографическая ссылка
Мазуркин П.М. ВЛИЯНИЕ КООРДИНАТ И ВЫСОТЫ ПОЛОЖЕНИЯ У ЦЕНТРОВ СТОЛИЦ УРАЛА И СИБИРИ НА ПАРАМЕТРЫ КЛИМАТА И ПОГОДЫ // Успехи современного естествознания. 2021. № 7. С. 47-53;URL: https://natural-sciences.ru/ru/article/view?id=37661 (дата обращения: 06.02.2026).
DOI: https://doi.org/10.17513/use.37661





