Тепловой режим горных выработок подземных сооружений криолитозоны, как горнодобывающего профиля (шахты и рудники) [1–3], так и другого назначения (подземные склады, холодильники, защитные объекты) [4–6] зачастую является определяющим фактором их надежной и безопасной эксплуатации. Это связано как с зависимостью прочностных свойств вмещающих мерзлых горных пород от температуры [7–9], так и существенным влиянием подземного микроклимата на комфортность и безопасность труда персонала подземных объектов [10–12]. При проектировании подземных сооружений уделяется особое внимание таким важным аспектам, как прогноз температурного режима (определение глубины оттаивания) горных пород вокруг выработок и оценка закономерностей формирования теплового режима в основных воздухоподающих выработках и на рабочих местах [11–14]. Точность прогноза и надежность оценки во многом зависит от точности задания начальных условий [14, 15]. В частности, расхода воздуха в выработках и их геометрических характеристик – сечения, периметра и длины. Если для конкретной выработки геометрические характеристики точно задаются при проектировании и не изменяются при эксплуатации, то расход воздуха является переменной величиной в течение года. И его реальные значения, например, в рудниках криолитозоны могут отличаться в разы. Это обусловлено действием естественной тяги, которая может существенно изменить всю проектную систему вентиляции рудника, вплоть до опрокидывания вентиляционной струи.
Цель настоящей работы – определение корректирующего коэффициента для оценки изменения температуры воздуха в конкретных точках сети горных выработок при изменении расхода воздуха в них (при прочих равных условиях).
Материалы и методы исследования
Для определения температуры воздуха в выработке после изменения базового расхода воздуха в «k» раз воспользуемся простой формулой
t2 = qt1, (1)
где t2 – температура после изменения расхода воздуха в выработке, °С; t1 – температура при начальном (базовом) значении расхода воздуха, °С; q – корректирующий коэффициент. д.е.
Корректирующий коэффициент находится по формуле, полученной в результате обработки данных численных расчетов по прогнозу теплового режима на участке горной выработки:
q = exp(f(1 – 1/k^0,2)/Q^0,2)), f = mlu/1000. (2)
В формуле (2) приняты следующие обозначения: f – приведенная площадь поверхности участка выработки, м0,6/с0,2; u – периметр выработки на участке, м; l – длина участка выработки, м; m – коэффициент, зависящий от формы и вида крепи выработки, д.е.; k – степень изменения расхода воздуха, д.е.; Q – базовый расход воздуха в выработке, м3/с.
Используя формулы (1) и (2), можно оценить степень изменения температуры воздуха в зимний период в конце отдельной горной выработки при изменении расхода воздуха, не прибегая к трудоемким расчетам.
Представляет интерес оценить ошибку, возникающую при определении температуры в конечной точке при изменении расхода воздуха в выработке. Относительная процентная ошибка может быть определена по формуле
ε = 100abs(1 – q). % (3)
Допустимая в инженерной практике ошибка вычисления искомой величины составляет обычно менее 10 % или 0,1. Используя это допущение, из формулы (3), при подстановке в нее формулы (2), после несложных преобразований получена зависимость для определения соотношения между базовой величиной расхода воздуха и степенью его изменения для конкретной выработки:
k ≥ 1/(1 – 0,095Q0,2/f)^5. (4)
Результаты исследования и их обсуждение
Прежде всего, необходимо отметить, что при изменении расхода воздуха тепловой баланс выработки остается практически постоянным. Так как увеличение количества холода, накапливаемого породами в холодный период года, будет компенсироваться увеличением количества тепла, накапливаемого в теплый период года. Небольшая разница будет возникать только за счет того, что коэффициент теплоотдачи в зимний период незначительно больше, чем в летний [12]. Кроме того, простой анализ формулы (2) показывает, что зависимость корректирующего коэффициента от расхода воздуха имеет степенной характер с показателем степени, равным 0,2. Это означает, что увеличение базового расхода воздуха (до корректировки схемы проветривания рудника), например в 1,5 раза, приведет к изменению множителя в 1,08 раза. И, как следует из формулы, собственно корректирующий коэффициент составит 1,02 (при базовом расходе 20 м3/с и увеличении его до 30 м3/с, например). Максимальное значение степени изменения расхода воздуха в выработках не превысит 2,0. Это соответствует корректирующему коэффициенту, равному 1,04. Таким образом, следует ожидать, что изменения температуры в конечных точках будут незначительны, даже при большой степени изменения базового расхода воздуха. Однако полностью подтвердить данное утверждение возможно только всесторонним количественным анализом. Для этого по полученным формулам были проведены вариантные расчеты, результаты которых приведены в виде графиков на рис. 1–5.
На рис. 1 показано изменение корректирующего коэффициента в зависимости от степени увеличения «k» базового расхода воздуха в выработке (взято два значения: 100 и 50 м3/с) для различных значений параметра «f» – приведенной площади выработки.
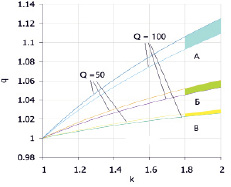
Рис. 1. Корректирующий коэффициент при базовом расходе 50 и 100 м3/с для различных участков выработки с приведенной площадью: А – 2,0; Б – 1,0; В – 0,5
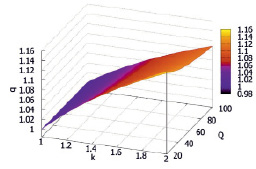
Рис. 2. Изменение корректирующего коэффициента в зависимости от степени увеличения Q
Как видно из графиков, приведенных на рисунке, увеличение базового расхода воздуха в два раза (с 50 до 100 м3/с) приводит к незначительному увеличению корректирующего коэффициента. Приведенная площадь играет более значимую роль, хотя в абсолютном значении эти цифры не очень велики. Например, изменение приведенной площади в 2 раза (с 1 до 2 – кривые А и Б) приводят к увеличению корректирующего коэффициента в 1,05 раза. А, при изменении приведенной площади в те же 2 раза (с 0,5 до 1 – кривые В и Б) приводят к увеличению корректирующего коэффициента в 1,02 раза. Но если сравнивать кривые А, Б и В, то очевидно влияние приведенной площади на корректирующий коэффициент: чем меньше приведенная площадь, тем кривые более пологие. То есть степень изменения корректирующего коэффициента при постоянном значении увеличения базового расхода, независимо от его величины, возрастает при увеличении приведенной площади выработки. Если провести горизонтальную линию, параллельную оси Х на отметке корректирующего коэффициента, равной 1,1, то получим, что при базовом расходе меньше 100 м3/с и изменении приведенной площади менее 2, увеличение расхода воздуха меньше, чем в 1,65 раза не приведет к ошибке в определении температуры больше допустимой в инженерной практике. Далее мы рассмотрим это вопрос более детально. На рис. 2 приведено изменение корректирующего коэффициента в зависимости от степени увеличения базового расхода воздуха для участка выработки с приведенной площадью, равной 2,0.
Как видно из рисунка, корректирующий коэффициент в большей степени изменяется в зависимости от степени увеличения базового расхода воздуха, чем от собственно абсолютного значения базового расхода. Об этом свидетельствует разный наклон плоскости на рисунке относительно осей Х («k») и У («Q»). Причем, как уже отмечалось, абсолютные значения корректирующего коэффициента не очень велики и находятся вблизи или ниже значений, допустимой в инженерной практике ошибки вычислений.
Для наглядности на рис. 3 и 4 приведены графики изменения температуры в конечной точке при различной степени увеличения базового расхода для участка выработки с приведенной площадью, равной 2,0. На рис. 3 для базовой температуры, равной -20,0 °С, а на рис. 4 для базовой температуры, равной -10,0 °С.
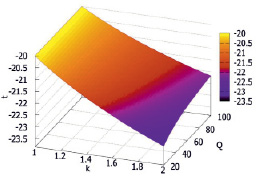
Рис. 3. Изменение температуры (-20,0 °С) при различной степени увеличения базового расхода для участка выработки с приведенной площадью, равной 2,0
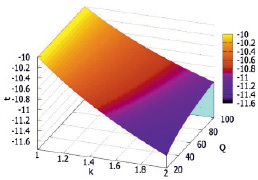
Рис. 4. Изменение температуры (-10,0 °С) при различной степени увеличения базового расхода для участка выработки с приведенной площадью, равной 2,0
Графики количественно подтверждают сделанный ранее очевидный вывод: чем ниже базовая температура в конечной точке, тем влияние степени увеличения базового расхода на изменение температуры сильнее. Причем это относится в большей степени к коэффициенту увеличения расхода воздуха, а не собственно абсолютному значению базового расхода.
На рис. 5 приведен график, характеризующий изменение допустимого значение коэффициента увеличения базового расхода воздуха для участка выработки с различной приведенной площадью.
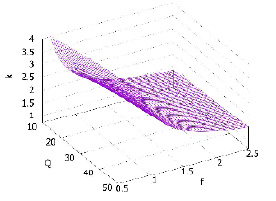
Рис. 5. Допустимое значение коэффициента увеличения базового расхода воздуха для участка выработки с различной приведенной площадью
Как видно из графика, чем больше приведенная площадь участка выработки, тем допустимое значение степени увеличения базового расхода меньше, независимо от значения самого базового расхода воздуха. Если значение коэффициента больше определенного по графику значения, то ошибка вычисления конечной температуры будет больше допустимой в инженерной практике (10 %). Во всех остальных случаях она будет меньше, и проводить корректировку температурного режима на участке выработки необязательно.
Заключение
На основе обработки данных численных расчетов получена простая аналитическая зависимость для определения корректирующего коэффициента температуры в конечной точке участка выработки при изменении базового расхода воздуха. Проведено сравнение точности и степени надежности предлагаемого подхода к оценке изменения температуры в горных выработках при изменении в них расхода воздуха. Предложенный подход позволяет получить достаточно достоверные данные для оценки изменения температуры в конкретной точке выработки, не прибегая к новым трудоемким расчетам и повторному анализу данных. Показано, что степень погрешности получаемых данных, как правило, не превышает допустимых в инженерной практике значений. Установлено, что корректирующий коэффициент в большей степени изменяется в зависимости от степени увеличения базового расхода воздуха, чем от собственно абсолютного значения базового расхода. При этом чем больше приведенная площадь участка выработки, тем допустимое значение степени увеличения базового расхода меньше, независимо от значения самого базового расхода воздуха. Результаты вариантных расчетов представлены в виде 2D и 3D графиков, которые позволяют в широком диапазоне условий проветривания горных выработок криолитозоны, характерных для золотодобывающих рудников, определить значения корректирующего коэффициента. Дальнейшие исследования в этой области должны быть направлены на сравнение результатов, полученных с помощью предложенного подхода с результатами, полученными с помощью численного прогноза значения температуры в конечной точке выработки при увеличении в ней базового расхода воздуха.
Библиографическая ссылка
Галкин А.Ф. ВЛИЯНИЕ РАСХОДА ВОЗДУХА НА ТОЧНОСТЬ ПРОГНОЗА ТЕМПЕРАТУРЫ В ПОДЗЕМНЫХ СООРУЖЕНИЯХ КРИОЛИТОЗОНЫ // Успехи современного естествознания. 2021. № 12. С. 101-106;URL: https://natural-sciences.ru/ru/article/view?id=37743 (дата обращения: 27.02.2026).
DOI: https://doi.org/10.17513/use.37743



