Для энергоёмких рудотермических печей переработки рудного сырья характерны повышенные температуры расплава, в котором происходят различные химико-технологические процессы, и в частности реакции восстановления с образованием газообразной окиси углерода, барботирующей сквозь расплав [1; 2]. Всплывающие пузырьки этого газа интенсивно перемешивают жидкостный расплав. Энергетическая эффективность химико-технологических процессов гетерогенного реагирования главным образом определяется тепловыми процессами массотеплопереноса, формирующими тепловой и гидродинамический профиль реактора, а также обеспечивает поставку реагента в зону реакции [3; 4]. Прямое экспериментальное исследование электротермических процессов затруднено труднодоступностью реакционной зоны, высокой температурой и т.д. Поэтому довольствуются фиксацией доступных извне параметров при обследовании режимов работы реакторов или изучением лишь низкотемпературных зон [5; 6]. Для численного моделирования весьма важна предварительная аналитическая оценка явлений, сопровождающих целевые процессы [7; 8].
В процессах восстановления с выделением газофазных продуктов в жидкости химические реакции зачастую определяют гидродинамическое состояние реакционного пространства [9; 10]. Ниже рассматриваются режимы реагирующей многофазной среды, где интенсивность процессов энергообмена во многом определяется барботирующими продуктами реакции в газофазной форме.
Качественный и количественный анализ особенностей теплоэнергетического и гидродинамического профиля высокотемпературной зоны протекания гетерогенных реакций рудотермической печи и расплава реагирующего рудного сырья, барботируемого газообразными продуктами реакций восстановления в виде пузырьков, позволяет описывать гидродинамику и теплоперенос системой дифференциальных уравнений с частными производными [11; 12].
Считается, что движение жидкой фазы провоцируется разностью плотностей жидкости за счет температуры, концентрации реагента и наличия газовой фазы в виде пузырьков [13; 14]. Рассматриваемая система представляется двумерной структурой: высотой H и шириной L, в виде дисперсного рудного шихтового материала с порозностью ε и жидкофазного расплава [15].
Цель работы заключается в математическом описании и расчёте характеристик конвективных потоков, формирующихся из-за изменения плотности, и влияния этих характеристик на теплоэнергетический и гидродинамический профиль высокотемпературной зоны рудотермической печи, где протекают эндотермические гетерогенные реакции восстановления.
Материал и методы исследования
Уравнения, описывающие движение фильтрующейся жидкости, перенос массы, тепла и газовой фазы в виде пузырьков, записываются в безразмерной форме:
∇υ = 0,
,
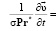
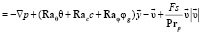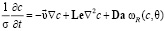, (1)
,
,
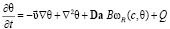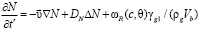здесь с – степень превращения,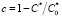 
, здесь C* и 
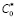– концентрации, конечная и начальная соответственно; t – безразмерное время 
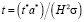, здесь t* – время, с; a* –температуропроводность, м2/с; σ – соотношение теплоемкостей 
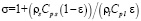; ρs, ρl – плотности носителя, твердого и жидкого соответственно; Cps, Cpl – теплоемкости твердого и жидкого носителя; ε – порозность; Le – безразмерный критерий Льюиса, 
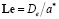, где De – коэффициент эффективной диффузии; Da – безразмерный критерий Дамкеллера, 
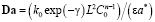, k0 – предэкспоненциальный множитель, γ = E / RT0 – безразмерная энергия активации, T – температура, R – универсальная газовая постоянная, индекс 
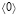обозначает начальные значения, 
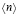– порядок реакции; θ – безразмерная температура, 
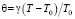; B – безразмерный тепловой эффект реакции, 
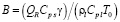; N – количество пузырьков; DN – коэффициент диффузии пузырьков; Vb – объём пузырьков, 
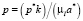, где p* – давление, Па; k – коэффициент проницаемости; μl – динамическая вязкость жидкости, Па с; 
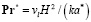, Pr* – критерий Дарси;
,
,
.
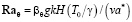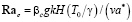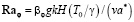βc, βφ, βθ – коэффициенты объемного расширения массового, термического и газофазного, с учётом изменения плотности из-за наличия газовой фазы.
Граничные условия имеют вид: c = θ = 0, при y = 0.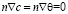 
для всех границ, а у боковой стенки рудотермической печи nυ = 0.
Учитывая малость коэффициента диффузии пузырьков DN и градиента ∇N, уравнение переноса газовой фазы представим следующими соотношениями:
,
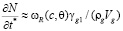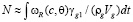. (2)
Отсюда получим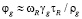 
, где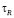 
– время пребывания пузырьков в слое.
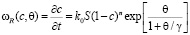(3)
Учитывая гетерогенную реакцию восстановления, как реакцию первого порядка, и раскладывая экспоненту в ряд до первого порядка, получим соотношение:
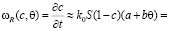
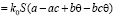, (4)
а тогда:
.
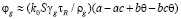Решение такой задачи даже численно представляет собой определенную трудность.
Для аналитического исследования поведения этой системы сделаем ряд упрощений. Рассмотрим слой, находящийся между горизонтальными плоскостями с температурами T0 и T1. Предполагая поставленную задачу стационарной и двумерной, учитывая, что скорость фильтрации жидкости невысокая, в уравнении движения можно пренебречь нелинейностью. Учитывая небольшие отклонения величин, входящих в уравнения, получим соотношения для:
υ = υ0 + υ1 , θ = θ0 + θ1 , c = c0 + c1.
А в состоянии равновесия принимаем равенство: υ = 0.
Уравнение для фильтрации записываем в виде:
.
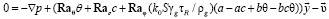Или при использовании возмущенной и линеаризованной формы:
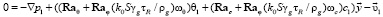. (5)
Используя оператор rot в уравнении движения для условий равновесия, то есть при скорости равной нулю, можно доказать одномерность по оси Oу распределения температур и концентраций. Зависимости температур и концентраций в равновесных условиях получаются экспоненциальными, в диапазоне температур от T0 до T1. Температурное и концентрационное поле в состоянии равновесия аппроксимируем линейной зависимостью, например для температуры: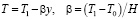 
.
После использования возмущенных компонент линеаризованные уравнения примут вид:
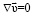
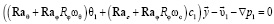
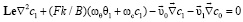(6)
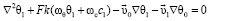
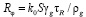, ωθ, ωc – коэффициенты, при разложении в ряд.
Описывая функцию тока ψ уравнениями: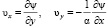 
, получим упрощенную запись для уравнений движения:
.
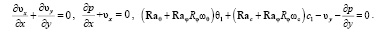И после исключения давления систему уравнений представим в форме:
,
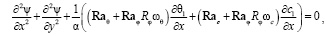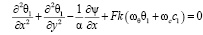, (7)
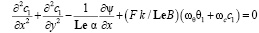
С учётом затухающих возмущений на границах, не покидающих рассматриваемую область, удаётся записать граничные условия в виде:
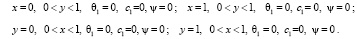(8)
Анализируя зависимость решений системы (7) от малых возмущений, будем строить решение, удовлетворяющее граничным условиям, следующим образом:
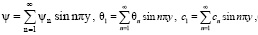(9)
где ψn, θn, cn – функции от х.
Подставляя выражения (5.9) в уравнения (5.7), получим:
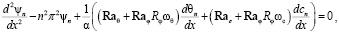
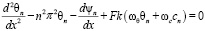, (10)
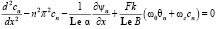
С граничными условиями:
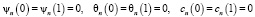. (11)
Из исходной системы уравнений (10) сформируем дифференциальное уравнение четвертого порядка относительно ψn, для этого первое уравнение системы (10) продифференцируем дважды по x и получим:
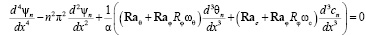(12)
Уравнения второго порядка для θn и cn системы (10) дифференцируем по x:
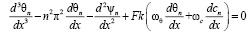
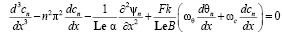
Подставляя выражения производных третьего порядка в уравнение (12) для функции тока:
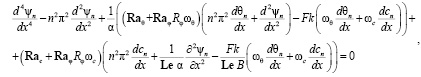
и объединяя множители, можно выделить следующие коэффициенты системы:
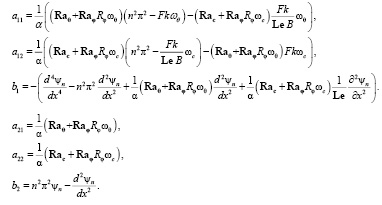
Таким образом, получается система линейных уравнений относительно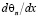 
, 
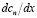. Далее, для полученных двух линейных уравнений, определяем соотношения для первых производных от температуры и концентрации, затем, подставляя в первое уравнение для функции тока, получим обыкновенное дифференциальное уравнение четвертого порядка, описывающее функции тока от х и у:
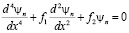. (13)
Учитывая, что решение (13) ищется в виде: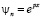 
, записываем характеристическое уравнение как: 
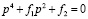. Обоснованно заключаем, что функции тока описываются гармоническими функциями вида: 
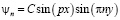, где C – произвольная const.
C использованием найденных функций тока определим компоненты вектора скорости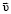 
:
.
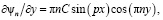
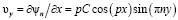Траектория движения газовой фазы математически описывается уравнениями: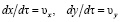 
, а траектория движения представляется равенством:
.
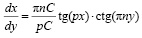Решением этого уравнения будет соотношение: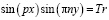 
, здесь: Tr = const, которую можно найти из начальных условий.
Результаты исследования и их обсуждение
Важное значение имеют изолинии, в которых Tr =0. Эти изолинии определяются уравнениями:
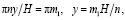
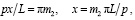
где m1, m2 ∈ Z.
Такие прямые делят зону реакций на множество отдельных ячеек. Жидкая фаза в виде расплава движется в этих ячейках, не покидая их пределов, так как компоненты скорости на границах ячеек равны нулю, то есть траектории движения жидкой фазы границ ячеек не пересекает (рисунок).
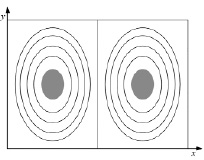
Структура траекторий движения жидкой фазы расплава в ячейке
Для каждой отдельной ячейки жидкая фаза движется внутри по замкнутой траектории вокруг ядра, внутри которого расплав неподвижен. Обнаруженная картина движения расплава в зоне гетерогенной реакции рудотермической печи качественно доказывает существование диссипативных структур в гидродинамических структурах. Она позволяет оценивать режим функционирования рудотермической печи, который образует вихревые потоки, формирующиеся под воздействием пузырьков газа. Пузырьки газообразной фазы барботируют сквозь жидкофазную среду расплава реакционной зоны рудотермической печи и интенсифицируют перемешивание и, как следствие, тепломассообменные и химико-энерготехнологические термически активируемые процессы.
Заключение
Установлено, что в реакционной зоне восстановительного реактора за счет образования газовой фазы возникают дополнительные факторы, влияющие на изменение плотности жидкой фазы и изменения архимедовой составляющей, значительно превосходящей по величине концентрационную и температурную. Поскольку скорость образования пузырьков и их количество зависят от температуры и концентрации, процессы перемешивания и энергообмена являются взаимосвязанными. Перемешивание является способом подачи массы реагента и повышения эффективности целевых процессов. Научно обосновано, что формирование микровихрей в ячеистой структуре реакционной зоны – интенсифицирует тепломассообменные и химико-энерготехнологические термически активируемые процессы.
При увеличении эквивалентного критерия Релея возникают новые траектории конвективного движения, что изменяет упорядоченное движение конвективных потоков и обеспечивает неустойчивость конвективного движения жидкой фазы расплава. Такой режим образует беспорядочный или турбулентный профиль движения жидкой фазы даже для систем, функционирующих в ограниченном объеме. Учет синергетических возможностей в такого рода системах позволяет программировать управляющие воздействия и более корректно обеспечивать достижение эффективного воздействия на целевые процессы.
Выводы
1. Показан механизм воздействия пузырьков газовой фазы, образующейся при протекании восстановительной реакции, на гидродинамику реакционной зоны.
2. Скорость реакции для линеаризованной экспоненты, представленная для возмущенных компонентов, сводит результирующее действие к сумме действия температуры и концентрации.
3. Получено, что воздействие газовой фазы сводится к воздействию температуры и концентрации, но это воздействие существенно эффективней.
4. Аналитически показано существование гидродинамических диссипативных структур, обеспечивающих перемешивание реагирующего расплава в реакционной зоне.
5. Таким образом, интенсифицирующее воздействие на процессы массопереноса заключается в основном за счет самой реакции восстановления, и, зная механизм воздействия, есть возможность рационально управлять такими процессами.
Разработанная гидродинамическая модель формирования микрослоя и его реагирования при контакте с твердым реагентом-восстановителем и анализ закономерностей протекания гетерогенных реакций при барботировании газа, выделяющегося в процессе реакций, учитывает полученные соотношения для критических условий массопереноса.
Исследование выполнено за счет гранта Российского научного фонда № 22-11-00335, https://rscf.ru/project/22-11-00335/.
Библиографическая ссылка
Бобков В.И., Никифоров В.А., Панченко С.В. ОСОБЕННОСТИ ГИДРОДИНАМИКИ И ТЕПЛОМАССОПЕРЕНОСА ПРИ АКТИВИЗАЦИИ ХИМИКО-ЭНЕРГОТЕХНОЛОГИЧЕСКИХ ПРОЦЕССОВ ВОССТАНОВЛЕНИЯ В КОКСОВОЙ ЗОНЕ РУДНОТЕРМИЧЕСКОЙ ПЕЧИ // Успехи современного естествознания. – 2022. – № 12. – С. 148-154;URL: https://natural-sciences.ru/ru/article/view?id=37963 (дата обращения: 19.04.2024).