Флуктуирующая асимметрия (ФА) – это ненаправленное отклонение от нуля величин билатеральных признаков при нормальном распределении их разности. Флуктуационная изменчивость встречается не только среди симметричных признаков, она может характеризовать количественную изменчивость биомассы, окраски и других параметров генотипической и фенотипической нормы реакции. По величине индекса ФА судят о стабильности развития как отклонении от гомеостаза развития популяции. Стандартная ошибка выборочных данных – обычная характеристика описательной статистики выборки индекса ФА, зависящая от ее величины и одновременно от ошибки измерения, допускаемой исследователем. Большая ошибка искажает величину с понижением статистической значимости ФА, что часто обусловлено присутствием направленной асимметрии (НА).
Отбор наиболее симметричных листьев позволяет провести измерение и сравнение такого признака, как ширина их половин. Проверка на направленную асимметрию часто показывает ее отсутствие даже при достаточно большом объеме выборки, например 50–100 листьев. При этом высокие показатели эксцесса и асимметричности свидетельствуют о примеси других видов асимметрии, включая антисимметрию [1]. Численно индекс ФА определяют по абсолютному значению отношения разности величин признаков к их сумме. Часто присутствие флуктуирующей асимметрии без примеси НА определяется только по одному признаку.
Метод геометрической морфометрии из-за большого количества меток и рандомного увеличения числа выборок повышает число степеней свободы в дисперсионном анализе в несколько сотен раз и нормализует выборку. В итоге исследователь получает направленную асимметрию, часто превышающую флуктуирующую, например по показателям среднего квадрата MS [2]. Такое обескураживающее проявление НА затрудняет поиск уровня стабильности развития, подтверждая множественность проявления асимметричности в выборке.
Увеличение числа промеров, фотографирований и образцов в выборке снижает ошибку измерения. Преимущество Прокрустового (морфогеометрического) анализа с повторными измерениями бесспорно. Остается, тем не менее, нерешенным вопрос, как исключить направленную асимметрию при сравнении двух и более выборок. Исследования видов рода Padus Mill. показали чувствительность листовых пластин к автомобильным выбросам [3]. Поиск дополнительных индикационных признаков [4] для детального анализа экологического состояния окружающей среды продолжается [5].
Сочетание обоих видов асимметрии отмечено в сообществах многих растений, включая популяции липы мелколистной и березы повислой [6, 7]. Ручное или электронное измерение признаков лишь иногда позволяет выделить направленную асимметрию в t-тесте. При нормальном распределении разности (L–R) величину НА экстрагируют из разности по формуле |L–R|–(L–R)av, где L и R – величины левого и правого гомологичных признаков, а (L–R)av – среднее значение выборки |L–R| по абсолютному значению [8].
Таким образом, для исследователя, не ставящего задачей тестирование особенностей формы листа видов с примесью направленной асимметрии, вполне приемлемы измерение линейных (угловых) признаков и определение «чистой» ФА.
Нам представляется наиболее сложной задачей определение формы распределения выборки. Даже при аккуратном сборе листовых пластин каждая популяция обладает особенностью частотного распределения значений (L–R). Что делать, если из двух выборок одна распределена по гауссовскому нормальному закону, а другая имеет логнормальное, или экспоненциальное распределение?
Исходя из представленной выше проблемы, нами сформулирована цель исследования – определение «чистой» ФА мерных признаков в выборках с отклонением от нормального распределения. Задачей работы является сравнение величин ФА между выборками с частотным распределением разности (L–R), отличающимся от нормального распределения, и составление соответствующих рекомендаций.
Материалы и методы исследования
Исследованы две популяции черемухи обыкновенной (Prunus padus L.) урбанизированных территорий площадью около 2–3 км2 в Московской области (город Электросталь, 55°48′ с. ш., 38°27′ в. д.) и городе Владимир (56°08′00″ с. ш., 40°25′00″ в. д.). Для сравнения использована северная популяция с Кольского полуострова (Мурманская область, город Апатиты, экспериментальный участок ПАБСИ, 67◦34́ 48́ ́ с. ш., 33◦18́ 10́ ́ в. д.).
Листья черемухи, близкие по величине, собраны в августе 2022 года с нижних частей крон деревьев. Методика сбора, сушки листьев и их фотографирования описана в предыдущей работе [9]. Проведено трехкратное измерение в сантиметрах только одного признака – ширины половины листа (экранный дигитайзер Dig2.31; пакет TPS, Rholf, 2017). Результаты перенесены в таблицы Excel, где выполнены первичные статистические анализы, из которых наиболее важными мы считаем характеристику частотного распределения (L–R) и нормированной разности (индекса ФА), определяемой по формуле |L–R|/(L+R).
Двухфакторный анализ проведен в программе STATISTICA 10 (Stat. Ink). Использован раздел ANOVA – факторный анализ. В этой же программе проведена подгонка (distribution fitting) c определением типа распределения выборок. Непараметрический анализ Колмогорова–Смирнова (K-S test) служил для определения нормальности распределения, а корреляционный анализ Спирмена – для определения зависимости индекса ФА от величины признака (L+R)/2. Везде принимался статистический уровень значимости 95%.
Результаты исследования и их обсуждение
Описательная статистика
Стандартная ошибка измерений левого и правого признаков в электростальской популяции была больше, чем во владимирской, и зависела от величины дисперсии и самого размера признака (больше признак – больше дисперсия – больше стандартная ошибка).
Распределения (L–R) и FА=|L–R|/(L+R) отличались от нормального (K-S test: p<0,05), но в электростальской популяции эти отличия более выражены. Значения эксцесса и асимметричности распределения частот представлены в таблице 1.
Деревья в популяциях не различались по значению ФА (F=1,2; p>>0,05), а величина признака различалась только в электростальской популяции (df=5; F=15,5; p<<0,01).
Корреляционная статистически значимая зависимость между размером признака и величиной ФА не установлена, за исключением слабо выраженной отрицательной связи между (L+R)/2 и ФА. Это позволило сравнить две популяции с разными по величине листовыми пластинами. Направленная асимметрия не была выявлена (t-тест нулевой гипотезы L=R; р>0,05), следовательно, такой мерный признак, как ширина половины листовой пластины, может быть использован для определения ФА (рис. 1).
Таблица 1
Основные показатели описательной статистики листовых пластин
|
Популяция |
n |
признак, см |
FA |
||||
|
среднее |
дисперсия |
асимметричность |
эксцесс |
К-S тест, p<0,05 |
|||
|
Владимир |
69 |
1,81±0,02 |
0,018±0,004 |
0,001 |
4,79±0,29 |
27,90±0,57 |
0,33 |
|
Электросталь |
65 |
2,10±0,04 |
0,012±0,002 |
0,0002 |
1,92±0,30 |
3,80±0,59 |
0,19 |
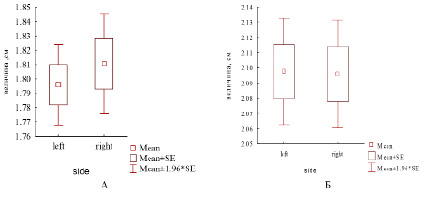
Рис. 1. Средние значения (Mean) и стандартная ошибка (SE) величины левого и правого признаков (А – Владимир, Б – Электросталь) и доверительный интервал среднего значения (mean±1,96*SE)
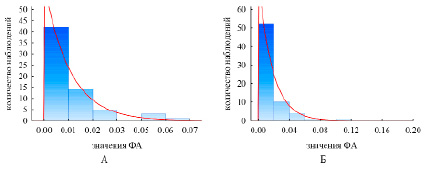
Рис. 2. Экспоненциальная форма распределения значений ФА (А – электростальская и Б – владимирская популяции)
Антисимметрия (как очень редкий тип асимметрии) не обнаружена. Мы считаем наиболее подходящим методом определения антисимметрии нахождение корреляционной связи между выборками L и R. При непараметрическом распределении обычно используют корреляцию Спирмена. Отсутствие значимой отрицательной корреляционной связи указывает на отсутствие антисимметрии. В нашем случае коэффициент r Спирмена оказался статистически незначимым (r=0,03; p=0,5).
Проверка распределения и нормализация выборок
В современных статистических программных средствах насчитывается более 30 видов (типов) распределения частот в исследуемых выборках. В программе STATISTICA предусмотрено семь основных типов распределения. Нами протестированы выборки ФА=|L–R|/(L+R), обладавшие непараметрическим распределением, тестом Колмогорова–Смирнова установлено отклонение от нормальности (p<0,01–0,02). Протестирована нулевая гипотеза о том, что исследуемая выборка не отличается по частотному распределению от предсказанной. Выявлен экспоненциальный характер распределения частот ФА с вероятностью не менее 5% (p=0,55 – Электросталь и p=0,13 – Владимир) (рис. 2).
Результаты других видов распределения были статистически незначимы. Логарифмированием с трансформацией по Боксу [10] получено нормальное распределение. При этом использована формула d=(|LgL–LgR|+0,00005)0.33, где d – величина преобразованной флуктуирующей асимметрии. Это преобразование предусматривает логарифмирование разности L–R и возведение в степень.
Трансформированные выборки были проверены на нормальность распределения и подтвердили справедливость гипотезы о его соответствии более чем на 80%. Проверка на логнормальное распределение соответствует гипотезе на 57%. Т-тестом не установлены различия средних значений между трансформированными выборками (d=0,32 – Владимир и d=0,33 – Электросталь). Таким образом, распределение ФА после трансформации наиболее близко к логнормальному и нормальному, что свидетельствует о присутствии мультипликативной ошибки, связанной с ростом листовых пластин [8].
Сравнительный анализ
Для сравнения ФА использована мурманская популяция. Для нее характерны гетерогенность в размерах листьев (F=9,2; p<0,001) и асимметричность на индивидуальном уровне (по отдельным деревьям; F=12,9, p<0,001). Распределение ФА характеризовалось как экспоненциальное (33%), и логнормальное (27%), направленная асимметрия отсутствовала. Величина FА=|L–R|/(L+R), превышала ФА популяций средней полосы и была равна 0,024±0,002 (Владимир – 0,018±0,004; Электросталь – 0,012±0,002; р<0,05). Непараметрическим тестом Вилкоксона установлено различие на уровне p=0,001. Характерным также является присутствие отрицательного эксцесса выборки ФА (γ=0,85±0,6), что может указывать на примесь антисимметрии. Гетерогенность в длине листовых пластин и их индивидуальная изменчивость в условиях севера, на первый взгляд, повышают асимметричность. Как показывают предыдущие исследования методом геометрической морфометрии, форма листовых пластин черемухи мурманской популяции очень изменчива, а их размеры меньше, чем в популяциях средней полосы России [2, 9].
Значительная стандартная ошибка измерения левой и правой половин листовых пластин черемухи (особенно электростальской популяции) объясняется их выраженным компенсаторным ростом. С этим связана высокая вероятность экспоненциального распределения, которое нормализуется даже после простого нахождения разности логарифмов по основанию 10: LgL–LgR. Такой метод нормализации применим, но не для всех выборок. Если у выборки высокий показатель эксцесса, то применяют нормализацию по Боксу, также не являющуюся панацеей от непараметрического распределения. В таких случаях важно избегать выбросов, дающих «хвост» в распределении значений ФА. Так, владимирская популяция с высокими значениями асимметричности и эксцесса обладает примесью других видов распределения, возможно, дискретных, т.е. прерывистых – Пуассона или Бернулли. При предварительной инспекции данных гербарных материалов важна картина распределения выборочных величин L и R. Высокие показатели дисперсии, асимметричности (скоса) и эксцесса значений ФА часто свидетельствуют об отклонении от нормального распределения, когда становится невозможным сравнение по средним арифметическим данным.
В сравнительном аспекте мерный способ определения ФА прост и достаточно надежен. Для окончательного результата мы рекомендуем использовать двухфакторный анализ (особь × сторона). Его достоинство состоит в высокой степени свободы при определении ошибки, т.е. доли необъясненной дисперсии. Результаты двухфакторного анализа приведены в таблице 2.
Наибольшая ошибка (ФА10; p>0,05) была получена для мурманской популяции из-за высокой гетерогенности линейных параметров листовых пластин. В электростальской популяции большая стандартная ошибка выборки и экспоненциальность распределения также привели к росту ошибки взаимодействия особь × сторона. И только одна владимирская популяция обладала статистически значимой флуктуирующей асимметрией (индекс ФА10).
Чистую ФА можно получить даже при повышенных значениях эксцесса (γ=2–3), но не настолько высоких, чтобы вызвать большую ошибку необъясненной дисперсии. Отклонение от нормальности, которую постоянно необходимо проверять, – это следствие высокого эксцесса, т.е. выбросов отдельных значений (варианс) за пределы доверительного интервала.
Метод геометрической морфометрии подтвердил отсутствие ФА в мурманской популяции, высокая изменчивость формы здесь сопряжена с низким проявлением асимметрии. По нашему мнению, этот факт не говорит о стабильном развитии данной популяции, а лишь характеризует ее гетерогенность в условиях северного региона.
Рекомендации для мерного определения ФА:
1) максимально приближать размеры листьев, собираемых в различных локалитетах;
2) проверять выборки на нормальность распределения разности (L–R);
3) делать троекратные измерения для определения стандартной ошибки;
4) проверять нормализующий метод оценки ФА в двухфакторном дисперсионном анализе.
Таблица 2
Результаты двухфакторного анализа особь × сторона (ФА10)
|
SS |
Degr. of |
MS |
F |
p |
|
|
Владимир |
2,093 |
68 |
0,031 |
3,0 |
0,000 |
|
ошибка |
2,811 |
276 |
0,010 |
||
|
Электросталь |
0,186 |
59 |
0,003 |
1,1 |
0,306 |
|
ошибка |
0,688 |
240 |
0,003 |
Примечание: SS – сумма квадратов; df – степень свободы; MS – средний квадрат; F – критерий Фишера
Библиографическая ссылка
Зыков И.Е., Баранов C.Г., Прокопенко А.Д. СТАНДАРТНЫЕ ОШИБКИ ИЗМЕРЕНИЯ, ВИДЫ РАСПРЕДЕЛЕНИЯ ВЫБОРОЧНЫХ ДАННЫХ И ТИПЫ АСИММЕТРИИ ЛИСТОВЫХ ПЛАСТИН ЧЕРЕМУХИ ОБЫКНОВЕННОЙ (PRUNUS PADUS L.) // Успехи современного естествознания. 2023. № 2. С. 24-29;URL: https://natural-sciences.ru/ru/article/view?id=37994 (дата обращения: 17.02.2026).
DOI: https://doi.org/10.17513/use.37994



