В связи со сложностью политической ситуации в РФ становится актуальным импортозамещение не только в технологической, но и в сырьевой области. В частности, РУСАЛ планирует замещение импорта глинозема из-за рубежа его производством из небокситового сырья на территории РФ. В 2018 г. на Ачинском глиноземном комбинате РУСАЛ произвел 1,069 млн т глинозема из уртитовых руд. В 2023 г. РУСАЛ планирует создание опытно-промышленного производства в Ачинске по получению глинозема из каолина и к 2034 г. доведение производства глинозема до 1 млн т. Помимо каолина в качестве предполагаемого сырья рассматривается зола [1].
В ИГиП ДВО РАН разрабатывается фторидно-аммониевая технология переработки небокситового алюмосиликатного сырья, которая может успешно использоваться для золошлаковых отходов предприятий теплоэнергетики в связи с их накоплением в золоотвалах ТЭС Амурского региона [2–4]. Отметим, что зола приравнивается к полезным ископаемым, находящимся на поверхности Земли и содержащим большое количество ценных элементов, редкоземельных элементов, поэтому, например, ее изучение вызывает большой интерес [2; 5].
Целью данной работы является расчет кинетических характеристик топохимических реакций спекания золы с гидродифторидом аммония (ГДФА) и разложения с улетучиванием и сублимацией фторидно-аммониевых солей в процессе термообработки их спека с определением зон и уравнений протекания данных реакций.
Материалы и методы исследования
Фторируемым реагентом для химической реакции спекания выбрана электромагнитная фракция золы состава в мас. %: SiO2 – 54,27; Al2O3 – 21,01; Fe3O4 – 7,82; TiO2 – 0,66; CaO – 8,24; MnO – 0,30; MgO – 2,49; Na2O – 0,40; K2O – 1,23; P2O5 – 0,08; SO3 – 0,27; п.п.п. – 2,91 [2]. ЭФ составляет 88,7 мас. % пробы золы из золоотвала Благовещенской ТЭЦ и характеризуется высоким содержанием глинозема и низким содержанием серы. Экспериментальная реализация химических реакций фторирования и разложения с улетучиванием и сублимацией детально описана в [2]. Данная статья посвящена расчету кинетических и статистических характеристик исследуемых реакций.
Расчет проводится с применением параметрического регрессионного и корреляционного анализов с проверкой ряда статистических гипотез Фишера и Стьюдента [6, c. 352]. В качестве параметрических функций αi(t) выберем степенной (i = 0) и экспоненциальный (i = 2) законы, относящиеся к уравнениям ускоряющегося типа, уравнению Ерофеева – Авраами (i = 1) сигмоидного типа, а также уравнениям трехмерной диффузии замедляющегося типа (i = 3) и сжимающейся сферы (i = 4) геометрического типа
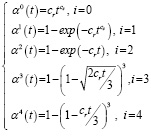, (1)
где αi(t) – i-я параметрическая функция, cr и cs – константа скорости и коэффициент формы кинетической кривой соответственно [7; 8, c. 438].
Регрессионные модели, строящиеся на основе нелинейных параметрических функций, также нелинейны. Модели для i = 0, 1, 2 строим аналогично работе [9], для моделей с i = 3, 4 учтем, что вместо проведения логарифмирования и решения уравнения регрессии с неравным нулю свободным членом, возможно сведение этих двух уравнений к регрессиям без свободного члена, угловой коэффициент в которых будет равен константе скорости cr. После проведения замен (2) и (3)
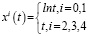(2)
и
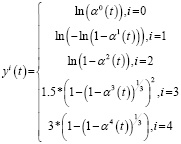(3)
получим линейную регрессионную модель для i-й параметрической функции
yi = (b0)i + (b1)i ∙ xi, (4)
где в формулах (2)–(4) индекс i (i = 0, 1, 2, 3, 4) нумерует линейные регрессионные модели, соответствующие параметрическим функциям αi(t); xi(t) и yi(t) – обобщенные абсциссы и ординаты; (b0)i и (b1)i – первый и второй коэффициенты соответствующей линейной регрессионной модели.
Точечные оценки коэффициентов линейной регрессионной модели (b*0 )ij и (b*1 )ij рассчитываются методом наименьших квадратов по уравнению (4), в котором
а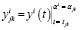 
,
индекс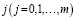 
нумерует исследуемые температуры Tj, 
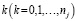– моменты отсчетов времени, tjk и αjk – массивы экспериментальных значений моментов отсчета времени и степеней превращения вещества, в общем случае размерностей (nj; m).
Точечные оценки (cr*)ij и (cs*)ij кинетических параметров cr и cs, соответственно, для i-й регрессионной модели при температуре Tj вычисляются по формулам
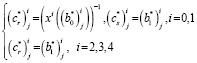
. (5)
Подставив точечные оценки параметров (cr*)ij и (cs*)ij в i-ю параметрическую функцию αi(t), при температуре Tj получим функцию отклика αij (t).
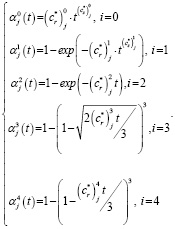(6)
Энергию активации (ЭА) Ei вычисляют по уравнению Аррениуса для констант скоростей [10, c. 83], которое представимо в виде уравнения линейной регрессии без свободного члена:
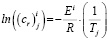. (7)
Предварительный выбор между регрессионными моделями (4) при каждой температуре выполняем по минимуму погрешностей аппроксимаций [6, с. 369], которые рассчитываются как относительные средние погрешности
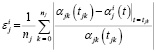, (8)
где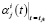 
– расчетные значения i-й функции отклика αij(t) в моменты отсчета времени tjk.
Расчет погрешностей коэффициентов линейных регрессионных моделей, имеющих интервальные оценки, осуществляется в соответствии с [6, с. 359]:
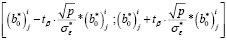(9)
и
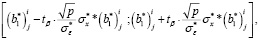(10)
где tβ – критические точки распределения Стьюдента [11] для уровня значимости β и числа степеней свободы p = nj – 2,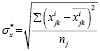 
, 
, 
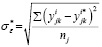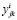и 
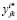– экспериментальные значения и ординаты линейной регрессии.
Как следует из формулы (5), погрешности кинетических параметров связаны с погрешностями коэффициентов линейной регрессионной модели, в частности погрешности констант скоростей (cr)ij совпадают с погрешностями коэффициентов (b1)ij для i = 2, 3, 4, а погрешности коэффициентов формы (cs)ij – с погрешностями коэффициентов (b1)ij для i = 0, 1. Относительные погрешности констант скоростей (cr)ij для i = 0, 1 в силу их логарифмической связи с постоянным членом (b0)ij равны его абсолютным погрешностям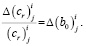 
Расчет статистических характеристик для проверки гипотез Фишера и Стьюдента с формулами для расчета проводится подробно в работе [9].
Результаты исследования и их обсуждение
Параметрические функции, выбранные при математическом моделировании химических реакций, получены исходя из предположений о сферической форме зародышей продукта. Дополнительно следует обсудить уравнение Ерофеева – Авраами. Следует заметить, что уравнение Ерофеева – Авраами, в силу того, что при замене переменных в нем возникает двойной логарифм, сглаживающий многие отклонения экспериментальных точек от линейной регрессии, обладает «широкой описательной способностью». Поэтому его применение должно быть осторожным и, в частности, недопустимым в случае противоречия с его физическим смыслом, например при наличии диффузионного торможения или в случае ускорения реакции в результате образования жидкой фазы [12, с. 50]. В нашем случае в реакции спекания золы с ГДФА фторирующий реагент при третьей и четвертой температурах находится в расплавленном состоянии. Поэтому применение уравнения Ерофеева – Авраами для реакции спекания допустимо только при нижних температурах, а также оно может использоваться для реакции разложения с улетучиванием и сублимацией фторидно-аммониевых солей.
Эксперимент с химическими реакциями фторирования и разложения с улетучиванием и сублимацией фторидно-аммониевых солей, как отмечалось выше, описан в [2], интегральные и дифференциальные кинетические кривые исследуемых реакций и их графики подробно обсуждены в [9]. Расчет в работе [9] проводился для параметрических функций с i = 0, 1, 2 в формуле (1). В данной работе авторы дополнили расчет функциями с номерами i = 3, 4 с соответствующим изменением всех формул.
Кинетические и статистические характеристики, полученные в результате предварительного отбора по величине погрешностей аппроксимаций, для реакций спекания золы с ГДФА и разложения с улетучиванием и сублимацией фторидно-аммониевых солей
|
Tj , °С |
50 |
100 |
150 |
200 |
350 |
450 |
550 |
|
(cr)ij , мин-1 |
0,000804 |
0,002356 |
0,003131 |
0,003787 |
0,017579 |
0,05915 |
0,071877 |
|
(cs)ij |
0,76 |
0,16 |
0,39 |
0,48 |
0,97 |
0,51 |
0,19 |
|
εij |
3 |
4 |
3 |
3 |
2 |
2 |
4 |
|
Ei, кДж/моль |
13 |
30.8 |
|||||
|
αi(t) |
Степенной |
Ерофеева – Авраами |
|||||
|
Зона реакции |
Диффузионная |
Переходная |
|||||
|
fj *(h1;h2) |
4,74 |
4,21 |
1,64 |
3,75 |
2.91 |
7.38 |
12.14 |
|
fβ (h1;h2) |
19,37 |
19 |
|||||
|
(f *)ji (p1;p2) |
2,0 |
3,59 |
2,9 |
3,72 |
5.42 |
2.42 |
1.49 |
|
fβ(p1;p2) |
4,46 |
10 |
|||||
|
t*(b0)ij |
94,28 |
25,36 |
12,83 |
1,12 |
4.05 |
34.27 |
20.65 |
|
t*(b1)ij |
39,19 |
7,66 |
12,19 |
4,4 |
67.08 |
20.61 |
6.61 |
|
(rxy)ij |
1 |
0,97 |
0,99 |
0,91 |
1 |
0.99 |
0.95 |
|
(tr)ij |
27,71 |
5,42 |
9,25 |
3,11 |
51.96 |
15.96 |
5.12 |
|
(tβ) |
4,3 |
3,18 |
|||||
Примечания: αi(t) – уравнение реакции, fj *(h1;h2) и fβ (h1;h2) – статистика и коэффициент Фишера для однородности дисперсии [13], (f*)ji (p1;p2) и fβ(p1;p2) – статистика и коэффициент Фишера для адекватности регрессии, t*(b0)ij и t*(b1)ij – статистика для свободного члена и углового коэффициента, (rxy)ij – коэффициент корреляции, (tr)ij – показатель согласованности Стьюдента, остальные обозначения в таблице как в тексте.
После расчета кинетики, выбора регрессионной модели с минимальной погрешностью аппроксимации и расчета статистических характеристик для выбранной модели проводим проверку пяти статистических гипотез регрессионного и корреляционного анализа: об однородности дисперсии воспроизводимости, об адекватности модели регрессии и о значимости ее коэффициентов, о практической ценности функции отклика и значимости коэффициента корреляции. При проверке гипотез соответствующие статистики рассчитываются и сравниваются с табличными значениями аналогично [9]. Результаты расчета кинетических и статистических характеристик приведены в таблице.
Из таблицы видно, что реакция фторирования золы ГДФА протекает при всех температурах по степенному закону в диффузионной зоне, а реакция разложения с улетучиванием и сублимацией фторидно-аммониевых солей – в переходной зоне по уравнению Ерофеева – Авраами. Проверка статистических гипотез показала, что для реакции спекания гипотезы об однородности дисперсии воспроизводимости и об адекватности модели регрессии выполняются при всех температурах. Гипотеза о значимости свободного члена выполняется только при трех нижних температурах, в то время как угловой член значим при всех температурах. Высокие значения коэффициента корреляции говорят о практической ценности функции отклика, а высокие значения показателя согласованности – о значимости коэффициента корреляции. Для реакции разложения с сублимацией фторидно-аммониевых солей проверка показывает, что гипотезы об однородности дисперсии воспроизводимости и об адекватности регрессионной модели выполняются при всех температурах, оба коэффициента регрессии значимы при всех температурах, функция отклика имеет практическую ценность, а коэффициент корреляции значим при всех температурах.
Заключение
Расчет кинетики топохимических реакций является неотъемлемой частью общей проблемы разработки фторидно-аммониевой технологии переработки минерального силикатного и алюмосиликатного сырья, а также золошлаковых техногенных отходов. Расчет проводился методом параметрического регрессионного и корреляционного анализов с выбором между параметрическими функциями по минимуму погрешностей аппроксимаций и с последующей проверкой статистических гипотез Фишера и Стьюдента с целью придания убедительности результатам расчета. При отдельных температурах наблюдается нарушение гипотез, что свидетельствует о необходимости как более тщательного подбора параметрических функций, так и нахождения новых параметрических функций. Вместе с тем описание хода химической реакции степенной функцией в случае спекания и уравнением Ерофеева – Авраами в случае разложения с улетучиванием и сублимацией, по-видимому, является достаточно хорошим приближением.
Библиографическая ссылка
Пушкин А.А., Римкевич В.С., Гиренко И.В. ТОПОХИМИЧЕСКАЯ КИНЕТИКА ФТОРИДНО-АММОНИЕВОЙ ПЕРЕРАБОТКИ ЗОЛОШЛАКОВЫХ ТЕХНОГЕННЫХ ОТХОДОВ // Успехи современного естествознания. – 2023. – № 9. – С. 77-81;URL: https://natural-sciences.ru/ru/article/view?id=38106 (дата обращения: 18.05.2024).