В настоящее время большое внимание уделяется развитию технологий БПЛА (беспилотных летательных аппаратов), особенно в контексте применения в гражданских отраслях. В сфере лесного хозяйства применение таких устройств позволяет решать целый комплекс задач, которые ранее проводились только натурно.
Одной из важных составляющих процесса лесопользования является выполнение перечетных работ по оценке диаметров растущих деревьев. При использовании БПЛА с достаточно высокой точностью можно определить радиусы и диаметры крон. Далее процесс дешифрирования состоит в переходе с помощью регрессионной модели к диаметру ствола на высоте 1,3 м. Необходимо отметить, что в перегущенных древостоях соотношение между диаметрами крон и диаметрами стволов носит еще более сложную специфику, которую необходимо учитывать. Без натурных измерительных работ невозможно выполнить оценку точности перечетных работ дистанционными методами.
Исследований по изучению соотношению диаметров крон и стволов деревьев проведено достаточно много, но они не учитывают специфику технологии БПЛА и проведены на локальных объектах. Так, в статье И.В. Толкач, О.С. Бахур приводится краткий анализ измерительного дешифрирования цифровых снимков с использованием геоинформационных систем [1]. Установлено, что существуют тесные связи между таксационными и дешифровочными показателями полога древостоя.
В результате совместного изучения и анализа таксационных и дешифровочных показателей на пробных площадях и таксационных выделах выявлена зависимость между средним диаметром крон и средним таксационным диаметром деревьев на высоте 1,3 м для различных пород. Определены взаимосвязи таксационного диаметра с таксационно-дешифровочными показателями древостоя, такими как высота и диаметр крон [2].
В условиях ленточных боров Прииртышья формирование полога древостоя сосняков начинается с 50 лет и продолжается до 80 лет. В результате формируются разновозрастные древостои. Данные насаждения характеризуются ступенчатой сомкнутостью полога. В большинстве эти насаждения являются двухъярусными и реже трехъярусными [3].
Отдельные публикации предлагают комплексное решение проблемы определения таксационных показателей и описаний с использованием дистанционных методов и ограниченных по объему наземных работ [4].
Широкое применение в лесохозяйственных исследованиях за рубежом находят регрессионные модели смешанных эффектов, которые показывают значительные преимущества перед классическими моделями фиксированных эффектов [5, 6].
Некоторые публикации предлагают обзор методик определения таксационных характеристик, в том числе и методы дистанционного зондирования [7, 8].
В другой статье авторы разработали систему обработки данных измерительного дешифрирования чистых сосновых древостоев Ia–II классов бонитета. Данная система подразумевает выполнение измерительного дешифрирования чистых сосновых древостоев на цифровых снимках с вычислением основных таксационных показателей древостоя с помощью регрессионных уравнений взаимосвязей между таксационными и дешифровочными показателями [9].
Для расчета массы крон деревьев березы можно применять модель, где в качестве независимой переменной используется аналог объема кроны дерева, моделируемого произведением квадрата диаметра на длину кроны. При этом связь между логарифмами массы крон и этим показателем можно аппроксимировать линейной функцией [10].
Следующая работа описывает методику дешифрирования таксационных показателей смешанных березово-еловых древостоев на сверхдетальных снимках, полученных с беспилотных летательных аппаратов в условиях северо-таежного лесного района [11].
Для молодняков ели, под пологом березняков южной тайги, находящихся в стадии возмужания и зрелости, составлены конкретные уравнения регрессии, которые могут применяться при проведении исследований в подпологовых популяциях ели [12].
В результате анализа научной литературы можно констатировать, что при всем разнообразии представленных вопросов о дешифрировании полога и переходе к морфологическим показателям отдельных деревьев вопросы соотношения диаметров крон и стволов в высокополнотных насаждениях представлены недостаточно и требуют отдельного исследования.
Материалы и методы исследования
Сосновые насаждения, произрастающие на территории учебно-опытного лесхоза СибГУ, имеют ряд особенностей, которые отличают их от других сосняков. Это происхождение и местоположение (значительное число древостоев сформировалось на старопахотных землях, размещены сосняки в водоохранной зоне р. Енисей, высокопродуктивные насаждения произрастают на южном склоне), сосняки характеризуются высокой полнотой и густотой, качество местопроизрастания имеет широкий спектр условий от I до IV класса бонитета. На рис. 1 представлена схема местоположения района исследования.
Рис. 1. Район исследований в Учебно-опытном лесхозе СибГУ на космическом снимке (выделенная часть сосновых насаждений характеризуется высокой густотой и полнотой)
Таблица 1
Коэффициенты корреляции связей морфологических признаков деревьев (диаметрами стволов) и показателями кроны сосны
|
Номер квартала |
Номер выдела |
Класс бонитета |
Коэффициенты корреляции |
|||||
|
направления радиусов крон |
||||||||
|
С – Ю |
С – З |
С – В |
Ю – З |
Ю – В |
З – В |
|||
|
51 |
12 |
I |
0,76 |
0,49 |
0,45 |
0,72 |
0,54 |
0,44 |
|
51 |
11 |
I |
0,92 |
0,86 |
0,88 |
0,86 |
0,90 |
0,84 |
|
51 |
10 |
I |
0,92 |
0,83 |
0,85 |
0,82 |
0,85 |
0,83 |
|
42 |
17 |
I |
0,89 |
0,87 |
0,91 |
0,90 |
0,90 |
0,90 |
|
50 |
19 |
I |
0,85 |
0,82 |
0,85 |
0,87 |
0,87 |
0,86 |
|
50 |
20 |
I |
0,77 |
0,76 |
0,67 |
0,69 |
0,66 |
0,59 |
|
43 |
14 |
II |
0,67 |
0,77 |
0,39 |
0,61 |
0,59 |
0,53 |
|
42 |
18 |
II |
0,59 |
0,70 |
0,80 |
0,34 |
0,67 |
0,76 |
|
42 |
19 |
II |
0,71 |
0,66 |
0,83 |
0,66 |
0,77 |
0,75 |
|
42 |
21 |
II |
0,81 |
0,80 |
0,81 |
0,82 |
0,77 |
0,73 |
|
43 |
13 |
III |
0,73 |
0,82 |
0,82 |
0,77 |
0,74 |
0,72 |
|
43 |
15 |
III |
0,78 |
0,88 |
0,89 |
0,79 |
0,85 |
0,80 |
|
41 |
18 |
III |
0,95 |
0,91 |
0,93 |
0,93 |
0,94 |
0,94 |
|
50 |
27 |
III |
0,92 |
0,91 |
0,94 |
0,92 |
0,92 |
0,89 |
Примечание: коэффициенты корреляции значимы, поскольку р < 0,05. Оценки получены при уровне доверительной вероятности 95,4 %. Ячейки с максимальным коэффициентом корреляции
Полевые работы проводились в сосняках I–III классов бонитета в насаждениях на 14 лесных участках (выделах). Измерялись радиусы крон в четырех направлениях (С – Ю, С – З, С – В, Ю – З, Ю – В, З – В) и диаметры стволов сосны на высоте 1,3 м.
Результаты исследования и их обсуждение
Корреляционная связь устанавливалась между диаметрами стволов и диаметрами крон в направлениях С – Ю, З – В и средним диаметром крон. В табл. 1 представлены коэффициенты корреляции связи радиусов крон по сторонам света.
Шкала оценки коэффициентов корреляции по Пирсону [13]. Согласно данной шкале связь между радиусами крон по сторонам света менялась от умеренной (0,34) до очень тесной (0,94). В отдельных лесных участках максимальная теснота связи наблюдалась по различным сторонам света.Оценка по классам бонитета показала, что различий крон по радиусам не наблюдалось.
Таблица 2
Коэффициенты корреляции связи диаметров стволов и диаметров крон деревьев сосны
|
Номер квартала |
Номер выдела |
Класс бонитета |
Коэффициенты корреляции dк – d1,3 |
|
51 |
12 |
I |
0,72 |
|
51 |
11 |
I |
0,71 |
|
51 |
10 |
I |
0,86 |
|
42 |
17 |
I |
0,90 |
|
50 |
19 |
I |
0,71 |
|
50 |
20 |
I |
0,64 |
|
43 |
14 |
II |
0,75 |
|
42 |
18 |
II |
0,83 |
|
42 |
19 |
II |
0,75 |
|
42 |
21 |
II |
0,89 |
|
43 |
13 |
III |
0,90 |
|
43 |
15 |
III |
0,93 |
|
41 |
18 |
III |
0,83 |
|
50 |
27 |
III |
0,85 |
Примечание: коэффициенты корреляции значимы, поскольку р < 0,05. Оценки получены при уровне доверительной вероятности 95,4 %.
Таблица 3
Параметры уравнений связи диаметров кроны (dк) и диаметров стволов (d1,3): dк = f (d1,3), d1,3 = f (dк)
|
Номер квартала |
Номер выдела |
Класс бонитета |
Уравнение |
|||
|
dк= f (d1,3) |
R2 |
d1,3 = f (dк) |
R2 |
|||
|
51 |
12 |
I |
dк = 0,048d1,3 + 2,3951 |
0,62 |
d1,3 = 12,823dк – 21,405 |
0,62 |
|
51 |
11 |
I |
dк = 2,2495e0,0262 d1,3 |
0,54 |
d1,3 = -0,9627dк2 + 13,77dк – –16,32 |
0,56 |
|
51 |
10 |
I |
dк = 0,9239d1,30,4713 |
0,82 |
d1,3 = 2,0883dк1,7195 |
0,81 |
|
42 |
17 |
I |
dк = 0,0018d1,32 + 0,0225d1,3 + + 1,5014 |
0,89 |
d1,3 = -0,382dк2 + 10,591dк – –6,6787 |
0,84 |
|
50 |
19 |
I |
dк = 0,6312d1,30,5391 |
0,71 |
d1,3 = 4,3555dк1,3143 |
0,71 |
|
50 |
20 |
I |
dк = 1,1426ln(d1,3) – 0,1549 |
0,60 |
d1,3 = 3,3071dк1,5859 |
0,60 |
|
43 |
14 |
II |
dк = 0,0003d1,33 – 0,0223d1,32 + + 0,5586d1,3 – 1,5644 |
0,68 |
d1,3 = -0,2417dк2 + 7,6706dк + + 0,141 |
0,57 |
|
42 |
18 |
II |
dк = 0,0001d1,33 – 0,0105d1,32 + + 0,3196d1,3 – 0,0825 |
0,76 |
d1,3 = 6,6404dк – 0,6936 |
0,69 |
|
42 |
19 |
II |
dк = 0,3968d1,30,6262 |
0,64 |
d1,3 = 7,0553dк1,0216 |
0,64 |
|
42 |
21 |
II |
dк = 0,0005d1,32 + 0,0827 d1,3+ + 0,9814 |
0,80 |
d1,3 = 0,2185dк2 + 5,1574dк + + 1,5015 |
0,79 |
|
43 |
13 |
III |
dк = 0,0001d1,33 – 0,0089d1,32 + + 0,3241d1,3 – 0,2221 |
0,84 |
d1,3 = -0,2856dк3 + 4,1117dк2 – –9,004dк + 13,514 |
0,85 |
|
43 |
15 |
III |
dк = 0,0005d1,32 + 0,0909d1,3 + + 1,2705 |
0,87 |
d1,3 = 6,7121dк – 2,7516 |
0,86 |
|
41 |
18 |
III |
dк = 0,0002d1,33 – 0,0178d1,32 + + 0,4966d1,3 – 1,4142 |
0,83 |
d1,3 = 0,208dк3 – 3,6011dк2 + +22,987dк – 20,274 |
0,74 |
|
50 |
27 |
III |
dк = -0,0018d1,32 + + 0,1836d1,3 + 0,3072 |
0,86 |
d1,3 = 4,0046dк1,3766 |
0,83 |
Перед выполнением моделирования параметров диаметров ствола и диаметров крон необходимо определить степень тесноты связи между этими показателями. Коэффициенты корреляции, отражающие данные связи представлены в табл. 2.
Данные таблицы показывают, что теснота между диаметрами стволов и диаметрами крон менялась от 0,64 до 0,90 (от значительной до тесной связи). Результаты позволяют выполнить моделирование данных морфологических признаков. По классам бонитета в сосняках III класса бонитета установлена более высокая теснота связи в сравнении с I и II классами бонитета.
С целью моделирования диаметров крон и диаметров стволов построены регрессии (точечные диаграммы), отражающие зависимости dк = f (d1,3), d1,3 = f (dк).
Для аппроксимации данных связей использовались уравнения полиномиального, линейного, экспоненциального, степенного видов, которые представлены в табл. 3. Коэффициенты детерминации менялись от 0,54 до 0,89. Все регрессии адекватны и достоверны. Уравнения таблицы можно использовать в тех или иных случаях для прогнозирования выходных переменных.
Для оценки степени различия представлена диаграмма, отражающая связь диаметров крон с диаметрами стволов деревьев сосны (рис. 2).
На рисунке видны различия по всем трем классам бонитета для исходной связи, на этом основании отдельно изображены линии для сосняков I, II, III-го классов бонитета. На основе предыдущего графического анализа построены диаграммы связи dк = f (d1,3), d1,3 = f (dк) для I, II, III-го классов бонитета (рис. 2).
Составлен ряд нормативов для определения диаметров стволов на высоте груди и диаметров крон деревьев для сосняков разных классов бонитета в условиях подтаежно-лесостепного района Средней Сибири (табл. 4, 5).
Таблица 4
Нормативная таблица по определению диаметра крон сосны по ступеням толщины
|
Ступень толщины, см |
6 |
8 |
12 |
16 |
20 |
24 |
28 |
32 |
36 |
40 |
|
Диаметр кроны, м |
||||||||||
|
I класс бонитета |
1,9 |
2,1 |
2,6 |
3,0 |
3,4 |
3,7 |
4,0 |
4,2 |
4,5 |
4,7 |
|
II класс бонитета |
1,7 |
1,9 |
2,2 |
2,5 |
2,8 |
3,2 |
3,7 |
4,1 |
4,6 |
5,1 |
|
III класс бонитета |
1,6 |
1,8 |
2,3 |
2,8 |
3,3 |
3,8 |
4,2 |
4,7 |
5,2 |
5,7 |
|
Максимальная средняя регрессионная разница, м |
0,3 |
0,3 |
0,4 |
0,5 |
0,6 |
0,6 |
0,5 |
0,6 |
0,7 |
1,0 |
|
Ступень толщины, см |
44 |
48 |
52 |
56 |
60 |
62 |
64 |
68 |
72 |
76 |
|
I класс бонитета |
5,0 |
5,2 |
5,4 |
5,6 |
5,8 |
5,9 |
– |
– |
– |
– |
|
II класс бонитета |
5,7 |
6,3 |
6,9 |
7,5 |
8,2 |
8,6 |
8,9 |
9,7 |
– |
– |
|
III класс бонитета |
6,2 |
6,7 |
7,2 |
7,6 |
8,1 |
8,4 |
8,6 |
9,1 |
9,6 |
10,1 |
|
Максимальная средняя регрессионная разница, м |
1,2 |
1,5 |
1,8 |
2,0 |
2,4 |
2,7 |
0,3 |
0,6 |
– |
– |
Таблица 5
Нормативная таблица по определению диаметра стволов сосны по ступеням толщины
|
Ступень диаметра кроны, м |
1,0 |
2,0 |
3,0 |
4,0 |
5,0 |
6,0 |
7,0 |
8,0 |
9,0 |
10,0 |
11,0 |
11,5 |
|
Диаметр ствола, см |
||||||||||||
|
I класс бонитета |
5,2 |
11,3 |
17,8 |
24,6 |
31,7 |
38,9 |
46,3 |
53,8 |
61,5 |
69,2 |
– |
– |
|
II класс бонитета |
7,0 |
13,8 |
20,3 |
26,6 |
32,8 |
38,7 |
44,5 |
50,1 |
55,4 |
60,6 |
– |
– |
|
III класс бонитета |
5,8 |
12,2 |
18,6 |
25,0 |
31,4 |
37,8 |
44,1 |
50,5 |
56,9 |
63,3 |
69,7 |
72,9 |
|
Максимальная средняя регрессионная разница, см |
1,8 |
2,5 |
2,5 |
2,0 |
1,4 |
1,1 |
2,2 |
3,7 |
6,1 |
8,6 |
– |
– |
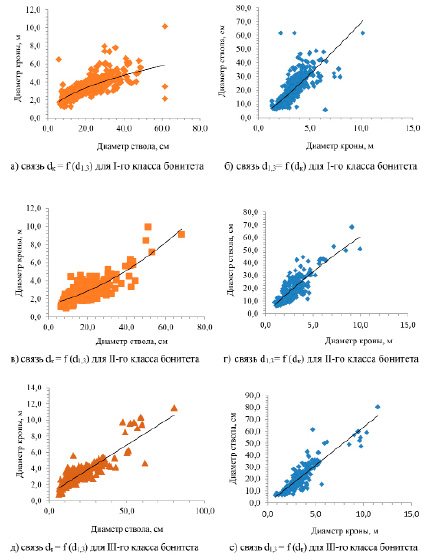
Рис. 2. Регрессионная связь диаметров стволов и диаметров крон сосны разных классов бонитета
Развитие крон деревьев разных ступеней толщины и по классам бонитета происходит разнонаправленно и зависит от того, в какой части высоты вертикального полога развивается крона (рис. 3, А). При этом динамика размера ствола дерева вне зависимости от качества условий местопроизрастания (класса бонитета) соответствует одной закономерности (угол наклона маловариабилен) (рис. 3, Б).
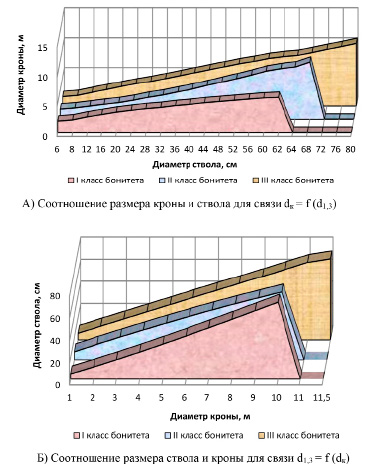
Рис. 3. Динамика изменения диаметров крон и стволов в зависимости от размера деревьев по диаметру стволов и крон с учетом классов бонитета
На этом основании и по причине особой важности связи d1,3 = f (dк) с точки зрения дешифровочных работ указанная связь линеаризована с помощью процедуры логарифмирования. Результаты представлены в табл. 6.
Все уравнения имели линейную форму после логарифмирования. Показатели детерминации менялись от 0,53 до 0,85. При этом все коэффициенты уравнений являлись значимыми (р < 0,05).
Основное внимание уделялось коэффициенту a, который в данном случае показывает угол наклона прямой линии. По данному показателю значительно отличались три лесных участка (51-12: 1,971; 51-10: 1,710; 50-20: 1,813).
Установлено, что данные три участка относятся к I классу бонитета и характерны для сосняков зеленомошного типа леса.
Все остальные коэффициенты варьировали в следующих пределах 0,869–1,314.
Диаграмма рис. 4 указывает на практически одинаковый угол наклона линий и близость прямых друг к другу.
Таблица 6
Параметры уравнения Lnd1.3= a*Lndк+b
|
Номер квартала |
Номер выдела |
Вид уравнения |
Коэффициент детерминации |
Уровень значимости |
|
43 |
13 |
Lnd1.3 = 1,088*Lndк + 1,6307 |
0,80 |
Все коэффициенты линейного уравнения значимы при р < 0,05 |
|
43 |
14 |
Lnd1.3 = 0,869*Lndк + 2,0213 |
0,53 |
|
|
43 |
15 |
Lnd1.3 = 1,039*Lndк + 1,6745 |
0,75 |
|
|
51 |
12 |
Lnd1.3 = 1,971*Lndк + 0,6149 |
0,54 |
|
|
51 |
11 |
Lnd1.3 = 1,114*Lndк + 1,4779 |
0,66 |
|
|
51 |
10 |
Lnd1.3 = 1,720*Lndк + 0,7363 |
0,81 |
|
|
42 |
17 |
Lnd1.3 = 1,206*Lndк + 1,689 |
0,79 |
|
|
42 |
18 |
Lnd1.3 = 1,078*Lndк + 1,7301 |
0,66 |
|
|
42 |
19 |
Lnd1.3 = 1,022*Lndк + 1,9538 |
0,64 |
|
|
42 |
21 |
Lnd1.3 = 1,031*Lndк + 1,7896 |
0,71 |
|
|
41 |
18 |
Lnd1.3 = 0,999*Lndк + 1,8771 |
0,71 |
|
|
50 |
19 |
Lnd1.3 = 1,314*Lndк + 1,4714 |
0,71 |
|
|
50 |
20 |
Lnd1.3 = 1,813*Lndк + 0,8949 |
0,81 |
|
|
50 |
27 |
Lnd1.3 = 1,306*Lndк + 1,4528 |
0,85 |
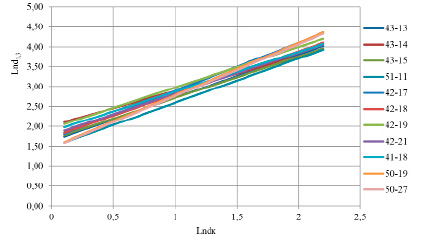
Рис. 4. Линии связи логарифма диаметров стволов и диаметров крон на лесных участках
Выводы
В результате выполненных исследований получены следующие выводы.
− Согласно шкале Пирсона, связь между радиусами крон по сторонам света менялась от умеренной (0,34) до очень тесной (0,94). По отдельным лесным участкам максимально тесная связь установлена в различных сторонах света. Оценка радиусов по классам бонитета показала, что различий крон с учетом качества условий местопроизрастания не наблюдалось.
− Теснота связи между диаметрами стволов и диаметрами крон менялась от 0,64 до 0,90 (от значительной до тесной связи). Результаты позволяют выполнить моделирование данных морфологических признаков. По классам бонитета в сосняках III класса бонитета выявлена более высокая по тесноте связь в сравнении с I и II классам бонитета.
− Составлены уравнения для вычисления диаметров крон и диаметров стволов на высоте груди. Коэффициенты детерминации моделей менялись от 0,54 до 0,89. Все уравнения адекватны и достоверны.
− Разработан ряд нормативов по определению диаметров стволов на высоте груди и диаметров крон деревьев для сосняков I, II, III-го классов бонитета в условиях подтаежно-лесостепного района Средней Сибири.
− Линеаризация изучаемых связей показала, что для всех сосняков применительно к прямым линиям регрессии характерен одинаковый угол наклона и близость прямых друг к другу, кроме сосняков зеленомошного типа леса I класса бонитета, где различия линий являются выраженными.
Таким образом, можно констатировать, что в перегущенных сосняках вне зависимости от качества условий местопроизрастания соотношение между диаметрами стволов и диаметрами крон имеют определенную схожесть в угле наклона и близости линий, с некоторым исключением для сосняков I класса бонитета зеленомошного типа леса.
Библиографическая ссылка
Вайс А.А., Козлов Н.В., Вараксин Г.С., Ануев Е.А. СООТНОШЕНИЕ ДИАМЕТРОВ КРОН И ДЕРЕВЬЕВ В ПЛОТНЫХ СОСНЯКАХ ПОДТАЕЖНО-ЛЕСОТЕПНОГО РАЙОНА СРЕДНЕЙ СИБИРИ // Успехи современного естествознания. 2024. № 2. С. 75-83;URL: https://natural-sciences.ru/ru/article/view?id=38221 (дата обращения: 14.02.2026).
DOI: https://doi.org/10.17513/use.38221



