В статистике существует такое понятие, как «представительность (репрезентативность)». Это свойство выборки, которое показывает, насколько хорошо данная выборка характеризует объект «в целом». Для того чтобы выборка была представительной, необходимо, помимо прочего, чтобы каждая проба, входящая в выборку, освещала приблизительно одинаковый объем недр [1, с. 38–43]. Следовательно, нужно, как минимум, чтобы разведочная сеть, по которой отбирались пробы, была бы равномерной во всех трех измерениях [2, с. 37–39]. Однако жизненный опыт геолога подсказывает, что описанная ситуация встречается крайне редко. На практике значительно более частой является ситуация, при которой в распоряжении геолога есть либо сети разных стадий разведки (например, сеть детальной разведки и сеть эксплуатационной разведки), либо участки сгущения в наиболее «интересных» местах. В результате наличия такой неравномерности использовать выборку «как есть» становится невозможным, поскольку пробы, составляющие выборку, характеризуют резко различные объемы недр. Подобная неприятная особенность пространственных данных называется кластеризацией [3]. Кластером обычно называют группу сближенных объектов. В данном случае такими объектами являются пробы, более подробно характеризующие участок, который по какой-либо причине показался геологу более интересным. Часто причиной повышенного интереса являются повышенные содержания в том или ином участке месторождения. В результате проявления подобного интереса в выборку попадает большее количество относительно богатых проб, что на гистограмме проявляется в виде искусственной полимодальности, обусловленной исключительно неравномерностью сети.
Наличие неравномерной сети опробования встречается на практике гораздо чаще, чем наличие равномерной регулярной сети. Но, учитывая необходимость использования данных и понимание невозможности их использования «как есть», возникает вопрос: что делать при наличии таких кластерных данных?
Целями исследования в данной статье являются рассмотрение действующих общепринятых вариантов решения проблемы кластерных данных и формирование единого и обоснованного подхода к выбору оптимальной сети декластеризации.
Материал и методы исследования
В качестве метода исследования были выбраны рассмотрение и сопоставление действующих общепринятых вариантов декластеризации данных, а также рассмотрение их преимуществ и недостатков.
Общепринятыми методами устранения кластеризации являются следующие подходы [4, р. 448]:
1) изменение выборки таким образом, чтобы она стала выборкой, отобранной по регулярной сети;
2) введение индивидуальных поправочных коэффициентов для каждой пробы, учитывающих неравномерность сети.
Оба предлагаемых способа подготовки данных к использованию носят название процедуры декластеризации, то есть являются тем действием, которое должно устранить кластеризацию.
Частичное разрежение сети
Первый путь – путь частичного разрежения сети, т.е., по сути, исключения части данных таким образом, чтобы получаемая выборка уже могла считаться выборкой, отобранной по равномерной сети. Проще всего это сделать, создав модель идеальной сети, а потом подогнать существующие данные под идеал. Например, можно создать геометрически правильную сеть из прямоугольных ячеек одинакового размера, а затем выбрать существующие данные либо:
• ближе всего к центрам полученных прямоугольных ячеек;
• случайным образом выбрав по одной пробе из ячейки.
Следовательно:
1) на существующую сеть данных накладывается сеть ячеек одинакового размера;
2) из имеющихся данных выбираются:
• либо только те, которые оказались ближе всего к центрам ячеек регулярной сети, а пробы, отстоящие от центра дальше, чем выбранная, исключаются из выборки;
• либо в каждой ячейке регулярной сети случайным образом выбирается проба, а остальные пробы исключаются из рассмотрения.
В итоге выполнения подобной декластеризации получается почти регулярная сеть данных, но возникает вопрос: а зачем тогда были потрачены деньги и время на сгущение сети, если потом все равно эти данные выброшены? Именно по причине исключения части данных, которые могут нести очень ценную информацию, подобный подход не рекомендуется к применению [5].
Введение поправочных коэффициентов
Второй путь – введение поправочных коэффициентов. Данные коэффициенты позволяют учесть неравномерность сети (кластеризацию) и при расчете статистических характеристик используются для взвешивания. Эти коэффициенты принято называть весами декластеризации. Использование весов является наиболее широко применимым способом учета неравномерности сети [6]. Декластеризация с помощью взвешивания обычно выполняется одним из двух наиболее часто употребимых способов:
1) полигональная декластеризация;
2) присвоение весов пробам.
Полигональная декластеризаци
При использовании этого метода каждая проба взвешивается на объем области, которую она освещает. Для этого необходимо геометризовать эту самую область. Разберем алгоритм для двумерного случая. Пусть у нас есть проба, для которой необходимо геометризовать область пространства, освещенную ею. Алгоритм полигональной декластеризации:
• для данной пробы находятся ближайшие соседи;
• отрезки, соединяющие эту пробу с ближайшими, делятся пополам;
• для всех отрезков строятся серединные перпендикуляры;
• через точки пересечения серединных перпендикуляров проводится контур той области пространства, которая характеризуется данной пробой.
В результате выполнения описанной операции каждая проба оказывается в центре некоторого многоугольника в двумерном случае или многогранника – в трехмерном. И это как раз и будет та область пространства, которая освещается данной пробой. Любая точка внутри данной области ближе к «центральной» пробе этой области, чем к любой другой пробе выборки. Весом каждой пробы в таком случае будет являться площадь этого многоугольника в двумерном варианте или объем – в трехмерном. Данные области называются полигонами Вороного.
У подобной декластеризации есть одна неприятная особенность: пробы на краю изученного пространства оказываются окружены слишком большой областью (просто потому, что за пределами опробованного участка нет проб, которые ограничат многоугольник) [7]. В результате пробы на краю исследованной области приобретают неправомерно большой вес (рис. 1).
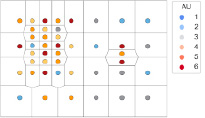
Рис. 1. Краевой эффект. Большая площадь полигонов на краях и, как следствие, некорректные веса у данных проб
Для минимизации краевого эффекта в программном обеспечении, в котором реализован этот алгоритм декластеризации, обычно пользователю предлагают ограничить максимальное расстояние, на которое растягиваются получаемые полигоны. Это могут быть контуры границ, каркасы рудных тел или просто предельное расстояние, задаваемое вручную. Необходимо заметить, что это ограничение, задаваемое вручную, несет в себе ощутимую долю волюнтаризма: на какое предельное расстояние тянуть полигон при отсутствии ограничений? 50 м? 100? 500?
Присвоение весов пробам
Рассмотрим также второй способ декластеризации, при которой вес пробе присваивается на основании количества проб в пределах ячейки регулярной сети. При таком варианте декластеризации в пределах изученной области создается идеальная модель равномерной регулярной сети [8]. Делается это, как и в предыдущих случаях, путем накладывания сети из ячеек одинакового размера прямоугольной формы (в двумерном случае) или ячеек в форме параллелепипеда (в трехмерном случае) на опробованную область. После этой операции в пределах каждой «идеальной ячейки» сети подсчитывают количество проб. Предполагается, что вес каждого прямоугольника или параллелепипеда равен 1. Тогда вес каждой пробы будет обратно пропорционален количеству проб в пределах данной «идеальной» ячейки. Следовательно, если в пределах ячейки оказывается две пробы, то вес каждой – 1/2, если 3 –1/3 и т.д. При наличии одной пробы в ячейке вес у нее будет равен 1.
В результате каждой пробе придается некий вес, а статистические характеристики рассчитываются с учетом взвешивания. К сожалению, в данном варианте декластеризации тоже есть свои минусы.
• При наличии неровных контуров исследуемой области (а они почти всегда такие) вес проб на краях опробованного пространства будет выше, чем в центре, даже при равномерной регулярной сети, потому что плотность та же, а опробованная область закончилась раньше, чем ячейка идеальной сети (рис. 2).
• Вес проб зависит от выбора начала отсчета «идеальной сети». Например, для ситуации, изображенной на рисунке 2, для отдельных краевых проб можно получить вес, равный 1, просто слегка сместив контуры «идеальных прямоугольников».
Чтобы исключить влияние этого фактора, в некоторых случаях проводят несколько шагов декластеризации, вводя систематическое смещение начала сетки. Веса, полученные после каждого шага смещения, нормируются на единицу, и результаты суммируются. Обычно бывает достаточно 5–10 смещений. По окончании манипуляций веса всех точек снова должны быть отнормированы так, чтобы их сумма была равна единице.
При выполнении такой декластеризации необходимо решить вопрос о размерах ячейки «идеальной сети». При этом «слишком большая» и «слишком маленькая» ячейки приведут к одинаковому результату, а именно – к выравниванию весов проб.
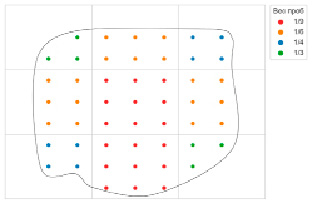
Рис. 2. Влияние контура рудного тела на веса проб
В случае слишком большой ячейкой все пробы попадают в одну из них, и вес каждой пробы в этом случае будет равен 1/N, где N – количество проб. Соответственно, декластеризованное среднее содержание будет равняться исходному среднему содержанию в пробах.
В случае слишком мелкой ячейки каждая проба занимает одну ячейку и вес каждой пробы равен 1, т.е. веса всех проб тоже одинаковы. Соответственно, декластеризованное среднее содержание, так же как и при варианте с одной ячейкой на всю рассматриваемую площадь, будет равняться исходному среднему содержанию в пробах.
Выбор оптимального размера ячейки декластеризации
Вопрос о выборе размера ячейки «идеальной сети» зависит от типа кластеризации.
Если данные кластеризованы случайным образом (есть области скопления проб, никак не связанных с их содержаниями), размер ячейки выбирается так, чтобы в областях с низкой плотностью опробования на одну ячейку приходилось приблизительно по одной пробе.
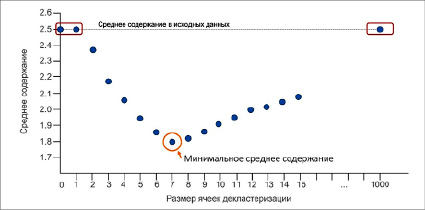
Рис. 3. Зависимость среднего содержания золота от размера ячейки сети декластеризации Четко видно минимальное взвешенное среднее содержание
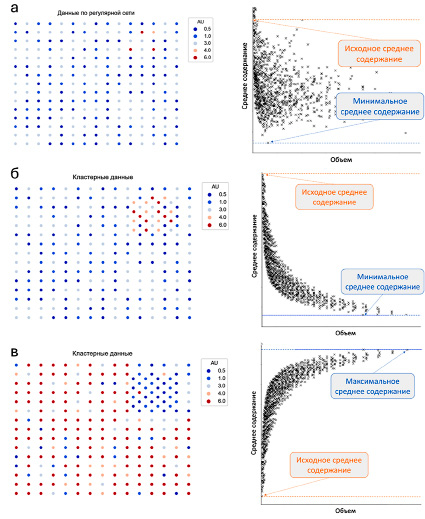
Рис. 4. а – зависимость между объемом ячейки и средневзвешенным значением не просматривается. Вероятнее всего, декластеризация не нужна; б – при увеличении объема ячейки происходит закономерное снижение средневзвешенного значения. Требуется декластеризация для компенсации влияния кластеризации в области высоких содержаний; в – при увеличении объема ячейки происходит закономерное повышение средневзвешенного содержания. Требуется декластеризация для компенсации влияния кластеризации в области низких содержаний
В случае же подозрения на наличие связи между содержанием и плотностью сети выполняется взвешивание по нескольким вариантам, задаваемым пользователем. Для этого производится построение графика зависимости среднего содержания от различных вариантов размера ячейки. На рисунке 3 представлен самый простой вариант, при котором анализируемые размеры ячеек сети декластеризации по всем трем осям одинаковы.
Обратите внимание, что первые два варианта размера ячеек приводят к одному и тому же результату, поскольку и при ячейке 1х1х1 м, и при ячейке 2х2х2 м внутрь каждой из них попадает только 1 проба. Соответственно, вес у всех проб будет равен единице, и взвешенное среднее содержание будет равно исходному среднему содержанию. Далее можно заметить, что при размере ячейки сети декластеризации 7х7х7 м достигается минимальное взвешенное среднее содержание. После данного значения взвешенное среднее содержание начинает стремиться к исходному среднему содержанию и достигает его при наличии только лишь одной ячейки на всю рассматриваемую площадь, т.е. 1000х1000х1000 м.
Рекомендуется не ограничиваться выбором единых размеров ячеек по всем трем осям, а анализировать все возможные варианты. В таком случае по оси X на данном графике следует отображать не размер ячейки декластеризации, а объем ячейки декластеризации, т.е. размер по оси X * размер по оси Y * размер по оси Z.
В результате серии взвешиваний в распоряжении геолога оказывается набор данных, которые можно представить как пары «объем ячейки декластеризации / средневзвешенное содержание» [9, с. 98–114]. График, построенный в этих двух осях, может быть близким к одному из вариантов, представленных на рисунке 4.
Результаты исследования и их обсуждение
После принятия решения о необходимости декластеризации требуется определить размер ячейки, которая будет использована для декластеризации. Предлагается два подхода к определению такого размера.
1. По соответствующей зависимости выбирается размер ячейки, при котором взвешенное среднее минимально (в случае наличия области высоких содержаний) или максимально (в случае наличия области низких содержаний). Если вернуться к первому, самому простому, случаю, то оптимальная ячейка декластеризации там составит 7х7х7 м. Если же наблюдается два и более минимальных взвешенных средних содержания, то выбирается наименьший размер ячейки декластеризации, при котором наблюдается минимальное взвешенное среднее содержание.
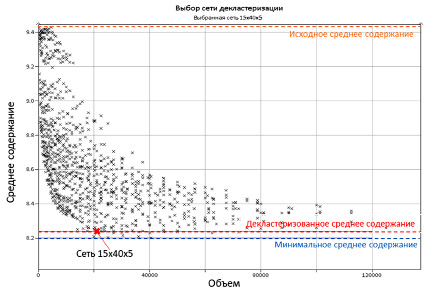
Рис. 5. Выбор оптимальной сети декластеризации, при котором среднее содержание «стабилизируется», т.е. график начинает выполаживаться
2. По соответствующей зависимости выбирается размер ячейки, при котором взвешенное среднее содержание стабилизируется (график начинает выполаживаться) (рис. 5).
Какой бы метод декластеризации ни использовался, обязательным условием является проверка качества проведенного процесса. Наилучшие способы – это визуальный анализ весов проб и сопоставление гистограмм.
Заключение
Исследование исходных данных опробования на кластерность является первоочередной задачей ресурсного геолога. Если в результате исследования кластерность данных подтверждается, то дальнейшая обработка исходных данных опробования без предварительной декластеризации приведет к смещенной оценке содержаний полезных ископаемых в модели минерализации.
Библиографическая ссылка
Вяльцев А.С. МЕТОДИКА ОПРЕДЕЛЕНИЯ ОПТИМАЛЬНОЙ СЕТИ ДЕКЛАСТЕРИЗАЦИИ ПРИ ОЦЕНКЕ МИНЕРАЛЬНЫХ РЕСУРСОВ // Успехи современного естествознания. 2024. № 5. С. 57-63;URL: https://natural-sciences.ru/ru/article/view?id=38266 (дата обращения: 31.01.2026).
DOI: https://doi.org/10.17513/use.38266



