Введение
Геоинформационные системы открыли новые горизонты в научных исследованиях. На ранних этапах развития метеорологии, климатологии и геоэкологии главным источником информации были инструментальные наблюдения, проводимые с помощью аналоговых приборов, таких как термометры, осадкомеры и барометры. Единственным статистическим методом обработки данных было их усреднение за определенные периоды – неделю, декаду или месяц. Однако такой подход не позволял учитывать пространственно-временные изменения параметров [1].
С появлением возможностей совмещения по времени однотипных наблюдений, а позднее – использования моделирования появилась возможность визуализировать распределение данных в пространстве в виде карты. Это значительно упростило анализ как пространственных особенностей процессов, так и динамики изменений.
Методы геостатистики, основанные на математических моделях и учитывающие пространственную автокорреляцию, позволяют не только создать поверхность интерполяции по наборам значений характеристик, но и оценить качество проведенной интерполяции в количественном выражении.
Ключевой моделью в геостатистике является кригинг, названный в честь инженера Д. Крига, который первым применил этот метод для анализа золотых месторождений в Южной Африке. Как продемонстрировал Д. Матерон, кригинг обеспечивает минимизацию суммы квадратов отклонений прогнозируемых значений от фактических значений пространственной переменной [2, с. 270]. Применение этого метода широко распространено в исследованиях воздействия атмосферного загрязнения для получения пространственных результатов оценок, в частности поступления веществ в природные экосистемы и сравнения с критическими нагрузками [3, c. 648].
Существует множество разновидностей кригинга: простой, ординарный, индикаторный, универсальный и др. В практической деятельности обычно применяют простой или ординарный кригинг. Основное различие между ними заключается в том, что при использовании простого кригинга предполагается, что детерминистическая компонента остается постоянной и известной на всей исследуемой территории. В то же время, при ординарном кригинге неизвестным остается среднее значение. Для локальных задач также выдвигается гипотеза о том, что среднее значение меняется только в непосредственной близости от точки оценки.
В данной работе представлено использование метода кригинга как одного из самых эффективных для моделирования, который позволяет создавать цифровую поверхность с высокой точностью даже в условиях неравномерного расположения сетей мониторинга, таких как наблюдения за химическим составом осадков (ХСО).
Целями исследования являются пространственное моделирование и анализ химического состава осадков на основе метода кригинга для территории Иркутской области с помощью геоинформационной системы SAGA.
Для достижения поставленной цели были решены следующие задачи:
1) сбор и систематизация многолетних данных о концентрациях загрязняющих веществ в атмосферных осадках на основе публикаций Главной геофизической обсерватории им. А.И. Воейкова;
2) изучение алгоритмов работы модуля кригинга в ГИС SAGA;
3) исследование влияния изменений параметров настройки кригинга на результаты интерполяции;
4) выбор оптимальных функций интерполяции данных методом кригинга для каждого года наблюдений.
Материал и методы исследования
В рамках эксперимента по интерполяции данных были использованы сведения о концентрациях загрязняющих веществ в атмосферных осадках на территории Иркутской области за несколько временных периодов: с 2003 по 2007 годы, с 2008 по 2020 годы и с 2010 по 2020 годы.
Такая периодичность обусловлена тем, что модуль в геоинформационной системе не позволяет проводить интерполяции с использованием точек, где были пропущены годы. Сами SDAT-файлы для дальнейшей оценки интерполяции были сформированы по годам.
Таким образом, в начале первого периода в регионе функционировали четыре станции мониторинга ХСО: Хамар-Дабан, Черемхово, Хужир и Саянск (без учета станции Иркутск). В 2008 году начали работать две новые станции – Исток Ангары и Байкальск, а в 2010 году – станция Большое Голоустное [4, с. 31; 5, c. 32].
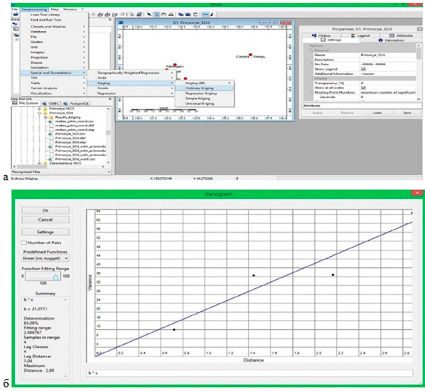
Рис.1. Расположение модуля ординарного кригинга в ГИС Saga (а) и вариограмма данных (б)
Для проверки точности интерполяции используется метод перекрестной проверки. Он заключается в том, что в процессе интерполяции исключается одна точка с уже известными данными, полученными по наблюдениям на этой станции. Далее проводится интерполяция в этой точке, и интерполированные значения сравниваются с данными, которые были исключены из процесса [6, с. 461].
Выбор программного комплекса SAGA обусловлен его преимуществами: он является дополнительной ГИС к основному комплексу QGIS, имеет открытый исходный код, который можно использовать для развития других ГИС, а также его можно скачать и использовать безвозмездно, что особенно важно для научных исследований [7, с. 57].
Метод кригинга можно выбрать в программе SAGA через меню Geoprocessing – Spatial and Geostatistica – Kriging – Ordinary Kriging (рис. 1а).
В настройках обычного кригинга необходимо указать слой, из которого будет происходить интерполяция, атрибут, который требуется интерполировать, а также границы эксперимента. В качестве точек для интерполяции используются станции ХСО, данные которых содержат сведения о координатах и концентрациях веществ за каждый год. Из атрибутов выбирается год, который подлежит интерполяции.
Можно ограничить границы эксперимента слоем с точками или указать пользовательские координаты. Для Иркутской области – это полигон с диапазоном границ от 100 до 109,5° в.д. и от 51 до 55° с.ш. Размер одной ячейки интерполированной поверхности составляет 0,001°. При указании необходимых параметров настройки автоматически производится расчет количества столбцов и строк предполагаемой поверхности. После подтверждения заданных параметров на экране появляется вариограмма (рис. 1б).
В геоинформационной системе SAGA работа с вариограммой осуществляется через выбор модельной функции (линейная, сферическая, Гаусса и др.) и диапазона ее установки – расстояния до конкретной точки, на которой будет проводиться аппроксимация [8, с. 179].
В качестве выходных данных ГИС предоставляет информацию о формуле, используемой в модели, а также о коэффициенте детерминации. Кроме того, на экран выводятся сведения о диапазоне установки в единицах измерения карты (обычно это единицы выбранной координаты), количестве образцов в этом диапазоне, количестве радиусов влияния (lag classes), расстоянии радиуса влияния и максимальной дистанции (рис. 1б).
Авторами было апробировано по 10 различных моделей интерполяционных функций для каждого года наблюдения в период с 2003 по 2020 годы, которые включали в себя линейную, линейную без эффекта самородка (linear non nugget), кубическую, экспоненциальную, Гауссову, логарифмическую, силовую, сферическую, квадратичную и стабильную модели [9, с. 33].
Таким образом, только для концентраций сульфатов в осадках в Иркутской области было получено 180 интерполяционных поверхностей (10 моделей * 18 лет), пример которых представлен на рисунке 2. Если добавить поверхности для нитратов, то общее их количество достигнет 360 (рис. 2).
Чтобы вычислить модельное значение в отсутствующей точке, авторы использовали QGIS для расшифровки SDAT-файлов. Для каждого года и типа модели были составлены таблицы с модельными значениями сульфатов и нитратов. Затем авторы создали итоговую таблицу, в которой сравнили исходные данные для рассматриваемого пункта и значения, полученные в результате интерполяции.
Результаты исследования и их обсуждение
При анализе первого набора данных интерполяции, который охватывает период с 2003 по 2007 годы и включает концентрации сульфатов в осадках, можно прийти к выводу, что лучшей моделью для этой задачи является Гауссова модель. Корреляция между этой моделью и исходными данными составляет 0,92, что является высоким показателем среди всех созданных интерполяционных моделей. Однако, учитывая небольшое количество станций, не удалось провести интерполяцию на 2007 год с использованием Гауссовой модели. Другие модели продемонстрировали менее удовлетворительные результаты:
- силовая и сферическая модели показали отрицательную корреляцию;
- кубическая модель не смогла провести интерполяцию, и ее результаты невозможно оценить;
- линейная и квадратическая модели оказались наименее качественными, их процент составляет менее 30%, что является низким показателем (табл. 1).
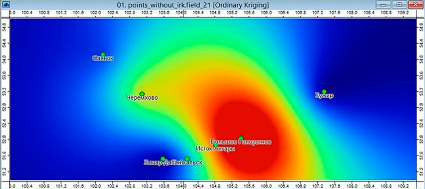
Рис.2. Результат интерполяции данных измерений компонента ХСО на территории Иркутской области в 2020 году
Таблица 1
Сравнение и корреляция модельных данных, полученных при использовании метода кригинга, с исходной информацией (измеренными значениями) для сульфатов на станции Иркутск
|
Годы |
Исходные данные |
Линейная («без самородка») |
Гаусса |
Логарифмическая |
Силовая |
Стабильная |
|
2003 |
6,28 |
12,82 |
10,68 |
10,62 |
10,68 |
|
|
2004 |
3,52 |
8,97 |
7,23 |
7,02 |
7,22 |
|
|
2005 |
3,44 |
5,98 |
5,19 |
4,51 |
4,77 |
|
|
2006 |
3,29 |
8,31 |
6,9 |
6,89 |
6,89 |
|
|
2007 |
6,19 |
4,84 |
4,13 |
5,23 |
4,64 |
|
|
2008 |
4,5 |
9,99 |
13,74 |
8,84 |
2318,38 |
14,49 |
|
2009 |
4,45 |
6,75 |
5 |
6,09 |
5,67 |
5,36 |
|
2010 |
7,08 |
8,91 |
6,35 |
8,5 |
17,07 |
7,59 |
|
2011 |
4,07 |
7,12 |
5,95 |
6,3 |
7,24 |
6,09 |
|
2012 |
4,27 |
6,38 |
6,86 |
6,25 |
4,72 |
5,96 |
|
2013 |
5,08 |
8 |
5,51 |
6,53 |
6,38 |
7,44 |
|
2014 |
5,35 |
8,95 |
8,14 |
9,02 |
7,24 |
7,82 |
|
2015 |
5,41 |
8,41 |
6,71 |
7,74 |
5,83 |
7,03 |
|
2016 |
5,53 |
8,93 |
6,69 |
7,91 |
4,76 |
8,24 |
|
2017 |
3,75 |
6,82 |
5,29 |
6,14 |
3,18 |
5,29 |
|
2018 |
3,64 |
6,99 |
8,53 |
6,71 |
–3,24 |
6,69 |
|
2019 |
5,06 |
7,82 |
6,03 |
7,25 |
5,35 |
7,59 |
|
2020 |
4,44 |
9,47 |
11,06 |
8,84 |
7,22 |
9,02 |
|
Корреляция 03 – 20 |
1 |
0,32 |
0,12 |
0,40 |
–0,12 |
0,22 |
|
Корреляция 03 – 07 |
1 |
0,21 |
0,92 |
0,28 |
0,32 |
|
|
Корреляция 10 – 20 |
1 |
0,67 |
-0,15 |
0,63 |
0,81 |
0,51 |
|
Корреляция 08 – 20 |
1 |
0,52 |
-0,14 |
0,54 |
–0,10 |
0,15 |
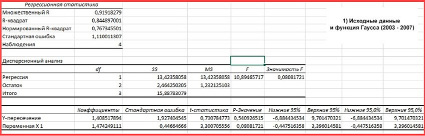
Авторами проведен анализ регрессионной статистики с использованием исходных данных и Гауссовой модели. Как и ожидалось, качество интерполяции оказалось на уровне 92%.
Коэффициент детерминации (R-квадрат) составил 0,84, что свидетельствует о том, что в 84% случаев модельные расчеты зависели от исходных значений на соседних станциях. Стандартная ошибка оказалась равной 1,11, что означает отклонение модельных данных от линии регрессии на 1,11 единицы (рис. 3(1)).
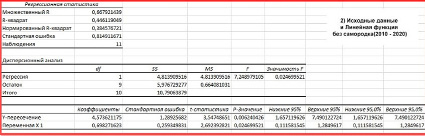
Анализируя результаты моделирования сульфатов за период с 2010 по 2020 годы, можно отметить, что силовая модель демонстрирует хорошие показатели корреляции. Коэффициент корреляции равен 0,81, что свидетельствует о качестве модели в 81%. Однако в проинтерполированных данных за 2018 год концентрация имеет отрицательное значение, что противоречит действительности. Также следует отметить, что полученные значения в 2010 году были значительно завышены – 17,07 мг/л.
На втором месте по качеству интерполяции расположилась линейная модель «без использования самородка». Ее корреляция с исходными данными составляет 67%, что является вполне удовлетворительным уровнем качества. Коэффициент детерминации равен 44% и демонстрирует, насколько исходные данные влияют на модель функции. Стандартная ошибка составляет 0,81 единицы. Р-значение регрессии меньше 0,05, что свидетельствует о статистической значимости интерполяционной модели (рис. 3(2)).
В ходе следующего эксперимента авторы рассмотрели период с 2003 по 2020 годы. Сравнивая исходные данные с функциями моделей, они пришли к выводу, что ни одна из них не соответствует 50%-му критерию качества.
1
2
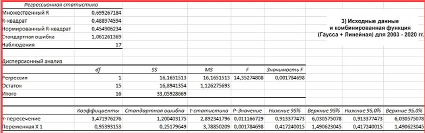
3
Рис. 3. Регрессионная статистика по сульфатам между исходными данными и модельными расчетами на ст. Иркутск по функциям: 1 – для функции Гаусса (2003–2007 гг.), 2 – Линейная функция (без самородка) (2010–2020 гг.), 3 – Комбинированная функция (Гаусса + Линейная) для 2003–2020 гг.
Кубическая модель наиболее близка к 50% (результат корреляции составляет 48%), однако из 18 лет наблюдения было смоделировано только 6. Из них 5 интерполяций относятся к периоду с 2010 по 2020 годы.
Линейная (без самородка) и логарифмическая модели демонстрируют качество 32% и 40% соответственно. Однако следует отметить, что хорошие результаты моделирования эти функции показали в период с 2010 по 2020 годы (~60%). В начальный период их корреляционная зависимость была крайне слабой (21–28%).
Таким образом, для оценки качества интерполяции в долгосрочной перспективе (18 лет) имеет смысл использовать различные функции.
Таблица 2
Корреляция модельных данных с исходной информации по нитратам на станции Иркутск методом Кригинга
|
Годы |
Исходные данные |
Линейная |
Линейная (без самородка) |
Кубическая |
Экспоненциальная |
Гаусса |
Логарифмическая |
Силовая |
Сферическая |
Квадратичная |
Стабильная |
|
2003 |
1,65 |
1,09 |
1,11 |
1,10 |
1,08 |
1,09 |
1,09 |
1,09 |
|||
|
2004 |
1,23 |
1,23 |
1,23 |
1,16 |
1,21 |
1,24 |
1,22 |
1,21 |
|||
|
2005 |
1,67 |
0,92 |
0,72 |
0,93 |
0,93 |
0,93 |
0,93 |
||||
|
2006 |
1,80 |
1,15 |
1,17 |
1,14 |
1,14 |
1,14 |
|||||
|
2007 |
2,83 |
1,16 |
1,18 |
1,16 |
1,16 |
1,16 |
1,16 |
1,16 |
|||
|
2008 |
1,96 |
1,32 |
1,51 |
1,34 |
1,39 |
1,25 |
1,39 |
1,24 |
1,37 |
1,39 |
1,34 |
|
2009 |
1,67 |
1,48 |
1,71 |
1,48 |
1,51 |
1,39 |
1,52 |
1,28 |
1,50 |
1,52 |
1,50 |
|
2010 |
2,08 |
1,68 |
1,63 |
2,26 |
1,51 |
2,98 |
1,70 |
1,69 |
1,69 |
1,53 |
|
|
2011 |
1,60 |
1,62 |
1,71 |
1,65 |
1,60 |
1,67 |
1,64 |
1,64 |
1,65 |
1,64 |
1,66 |
|
2012 |
1,65 |
1,86 |
1,86 |
2,04 |
1,70 |
2,07 |
1,78 |
1,74 |
1,87 |
1,62 |
1,82 |
|
2013 |
1,79 |
1,56 |
1,62 |
1,62 |
1,57 |
1,53 |
1,56 |
1,16 |
1,59 |
1,56 |
1,57 |
|
2014 |
1,91 |
2,11 |
1,95 |
1,90 |
6,94 |
1,84 |
1,41 |
2,27 |
2,18 |
0,88 |
2,26 |
|
2015 |
3,04 |
1,80 |
1,77 |
1,94 |
1,77 |
1,92 |
1,72 |
1,52 |
1,82 |
1,68 |
1,80 |
|
2016 |
2,65 |
1,63 |
1,58 |
1,50 |
1,60 |
1,57 |
1,55 |
1,37 |
1,49 |
1,47 |
1,56 |
|
2017 |
1,74 |
1,84 |
1,77 |
2,03 |
2,15 |
2,02 |
2,07 |
1,70 |
1,91 |
2,08 |
2,15 |
|
2018 |
1,29 |
2,15 |
2,13 |
2,29 |
2,29 |
2,32 |
1,96 |
2,34 |
2,07 |
2,27 |
2,54 |
|
2019 |
1,44 |
1,91 |
1,93 |
2,07 |
3,71 |
1,98 |
2,45 |
5,21 |
1,90 |
2,47 |
1,87 |
|
2020 |
1,71 |
1,86 |
2,10 |
1,97 |
1,98 |
1,97 |
1,92 |
1,76 |
2,26 |
1,91 |
1,98 |
|
Корреляция 03 – 20 |
1,00 |
–0,06 |
–0,10 |
–0,24 |
–0,06 |
–0,11 |
–0,16 |
–0,30 |
–0,27 |
–0,22 |
–0,15 |
|
Корреляция 03 – 07 |
1,00 |
0,04 |
0,12 |
0,69 |
0,09 |
–0,29 |
0,06 |
0,08 |
|||
|
Корреляция 10 – 20 |
1,00 |
–0,36 |
–0,52 |
–0,36 |
–0,16 |
–0,14 |
–0,45 |
–0,42 |
–0,37 |
–0,43 |
–0,44 |
|
Корреляция 08 – 20 |
1,00 |
–0,24 |
–0,45 |
–0,24 |
–0,14 |
–0,08 |
–0,38 |
–0,38 |
–0,27 |
–0,40 |
–0,35 |
В результате эксперимента и анализа корреляции авторы пришли к выводу, что для периода с 2003 по 2020 годы оптимальным решением будет использовать комбинацию Гауссовой и Линейной функций без самородка. Этот метод позволит получить наиболее точные интерполяционные данные по содержанию сульфатов.
Корреляция между исходными данными и результатами модели составила 0,70, а влияние соседних станций на моделирование – 0,48. Для станции Иркутск расчетные данные отклонятся от линии регрессии на 1,06 единицы.
Статистическая значимость F-критерия достигает 0,001%, что говорит о наличии очень сильной и статистически значимой связи между двумя типами данных (рис. 3(3)).
В ходе эксперимента по интерполяции нитратов авторами рассмотрены периоды с 2003 по 2007 годы, с 2010 по 2020 годы и с 2003 по 2020 годы в целом (табл. 2).
Нельзя однозначно утверждать, что какая-либо одна функция идеально подходит для интерполяции, поскольку в двух временных рядах (2003–2007 и 2010–2020) были обнаружены отрицательные значения корреляции.
В период с 2003 по 2007 годы зависимость модельных данных от исходных варьировала от 3 до 11% в зависимости от используемой модели. Поэтому авторы старались подобрать для каждого года наблюдения только ту модель, которая наиболее точно соответствует исходным данным, как показано на рисунке 4.
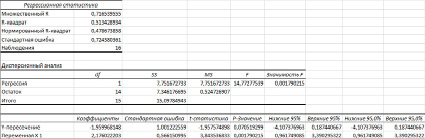
Рис. 4. Регрессионная статистика по концентрациям нитратов между исходными данными наблюдений и результатами комбинированных модельных расчетов на ст. Иркутск
В результате авторы объединили несколько интерполяционных моделей в единый ряд: для 2003 и 2005 годов использовалась Гауссова модель; для 2004 и 2009 годов – линейная модель без самородка; для 2006 года – логарифмическая модель; для 2008, 2011 и 2016 годов – линейная модель; для 2010, 2013 и 2014 годов – кубическая модель; для 2017 и 2020 годов – силовая модель; для 2018 года – сферическая модель; для 2019 года – стабильная модель.
Для 2007 и 2015 годов авторам не удалось подобрать подходящую модель интерполяции, так как расхождения между модельными и фактическими данными составили 1,5–2,5 раза.
Объединив различные модели в один ряд и проведя корреляцию с исходными данными, авторы получили качество интерполированного ряда на уровне 71%. Коэффициент детерминированности при этом составил 51%. Стандартная ошибка, отражающая отклонение ряда от прямой линии регрессии, равна 0,72. Уровень значимости F для модельного ряда оказался равным 0,001, что свидетельствует о статистической значимости регрессионной модели (рис. 4).
Выводы
1.Метод кригинга является наиболее приемлемым и информативным для моделирования пространственной интерполяции концентраций загрязняющих веществ в атмосферных осадках на региональном уровне.
2. Для периода с 2003 по 2007 годы, по данным четырех станций химического анализа осадков в Иркутской области, Гауссова функция оказалась лучшей для моделирования концентраций сульфатов на станции Иркутск.
3. Для десятилетия с 2010 года, когда количество станций мониторинга увеличилось до семи, оптимальной функцией стала линейная модель (без учета эффекта самородка).
4. Перекрестная проверка результатов моделирования с исходными данными за весь период с 2003 по 2020 годы выявила слабую корреляционную связь, а при выборе некоторых функций метода кригинга даже показала отрицательные значения корреляции результатов.
5. Для моделирования концентраций нитратов в период с 2003 по 2007 годы отлично подходит Гауссова функция, коэффициент корреляции составляет 0,69. В другие периоды наблюдается отрицательная корреляция по нитратам на станции Иркутск.
Заключение
Исследование показало, что метод кригинга является наиболее эффективным для моделирования пространственной интерполяции концентраций загрязняющих веществ в атмосферных осадках на региональном уровне. Для каждого года наблюдений требуется тщательно подбирать функцию, основываясь на модельной вариограмме.
Результаты исследования позволяют оценить уровень загрязнения атмосферных осадков и выявить источники выбросов. Это, в свою очередь, является основой для разработки и реализации природоохранных мероприятий, направленных на снижение антропогенного воздействия на экосистему.
Полученные данные представляют значительный интерес для ученых и специалистов в области экологии и охраны окружающей среды. Они могут быть использованы для проведения дальнейших научных изысканий и разработки новых методов мониторинга.
Библиографическая ссылка
Галушин Д.А., Громов С.А. ПРОСТРАНСТВЕННОЕ МОДЕЛИРОВАНИЕ И АНАЛИЗ ХИМИЧЕСКОГО СОСТАВА ОСАДКОВ НА ОСНОВЕ МЕТОДА КРИГИНГА (НА ПРИМЕРЕ ИРКУТСКОЙ ОБЛАСТИ) // Успехи современного естествознания. 2024. № 11. С. 30-38;URL: https://natural-sciences.ru/ru/article/view?id=38329 (дата обращения: 12.03.2026).
DOI: https://doi.org/10.17513/use.38329



