Введение
Мерзлые грунты представляют собой высокодинамичные системы, которые постоянно находятся в неравновесном состоянии, и любое, даже незначительное внешнее воздействие – температурное или механическое – способно вывести систему из равновесия. Установление закономерностей механического поведения таких грунтов осложнено многообразием сочетания влияющих факторов, определяющих процессы деформирования в грунтах. В дополнение к этому постоянно происходит изменение параметров системы в связи с протеканием различных внутренних процессов. В связи с этим для описания поведения грунтов под нагрузками в современной механике грунтов развиваются теории линейной и нелинейной вязкоупругости и вязкопластичности. Таким образом, механика мерзлых, талых и оттаивающих грунтов является важным и актуальным направлением исследований и областью прикладного применения в разделе механики деформируемого твердого тела [1, 2]. А на процессы ползучести и релаксации в инженерно-геологических исследованиях уже давно обращается внимание [3, 4].
Изучение процессов деформирования мерзлых и оттаивающих грунтов представляет собой достаточно трудную задачу. В определенной степени эти трудности объясняются наличием зависимости их механических свойств как от времени, так и от параметров процесса деформирования. Помимо того, в грунтах возникают необратимые остаточные деформации, что свидетельствует о необходимости применения методов теории вязкопластичности при исследовании процессов деформирования мерзлых и оттаивающих грунтов [3, 5].
Основная цель исследования состоит в разработке комплексной методики анализа кривых ползучести мерзлых и оттаивающих грунтов, используемой для обработки экспериментальных лабораторных исследований, что позволит моделировать и прогнозировать характер деформирования грунтов при изменении природных и техногенных условий.
Материалы и методы исследования
Поведение грунтов отличается тем, что в них одновременно присутствуют упругие, пластические и вязкие свойства. Для описания процесса деформирования грунтов используются механические модели, по которым составляются математические уравнения состояния [6, 7]. Принято, что деформация грунта является результатом наложения деформаций элементарных механических моделей идеализированных единиц. Для описания механического поведения реального грунта используются комбинации сочетаний простейших моделей, каждая из которых описывается одним физико-механическим свойством [6, 8].
На практике в инженерной геокриологии при исследовании процессов вязкопластического деформирования мерзлых и оттаивающих грунтов применяют, как правило, соотношения связи между напряжениями и деформациями, построенные путем структурного подхода с использованием упругих, вязких элементов и элементов сухого трения Сен-Венана. Таким способом созданы модели Бингама, Шведова, Ишлинского и некоторые другие модели вязкопластического тела [4, 9]. Стремление преодолеть некоторую ограниченность таких моделей обуславливает увеличение числа элементов в них, что, в свою очередь, существенно усложняет проблему определения характеристик используемых в моделях элементов, определяющих механические свойства деформируемых мерзлых и оттаивающих грунтов.
С целью решения этой проблемы при разработке моделей вязкопластического тела в работе введен обобщенный линейный элемент, поведение которого описывается интегральным соотношением Больцмана – Вольтерра:
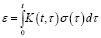 (1)
(1)
где ε – деформация, σ – напряжение, K (t, τ) – ядро интегрального оператора, характеризующее скорость деформации, t – время.
Основная идея теории ползучести состоит в том, что при каждой ступени нагрузки процесс протекает независимо от того, какая нагрузка была до, но принимается, что процесс деформирования не завершился. Таким образом, процесс деформирования многостадийный, и математическое уравнение выражено через сумму (интеграл) результатов всех этапов нагружения.
Данная теория позволяет учитывать ряд факторов – наследование предшествующего загружения, переменность нагрузок/разгрузок. Чем больше количество факторов, чем больше параметров в исходном уравнении. В целом уравнение состояния представляет связь между деформациями, напряжениями и временем [10, 11].
Простейшая модель вязкопластического тела на основе обобщенного линейного элемента составляется из последовательно соединенных звеньев (2), первое из которых представляет обобщенный элемент и элемент Сен-Венана. Элемент Сен-Венана представляет собой модель абсолютно жесткого тела до тех пор, пока действующее напряжение не достигнет определенной величины, после чего это тело теряет всякую способность сопротивляться действующим силам.
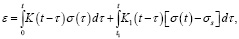 (2)
(2)
где K(t – τ), K1(t – τ) – ядра операторов для обобщенных линейных элементов первого и второго звеньев соответственно.
Механическое поведение рассматриваемой модели является вязкоупругим при значениях напряжений, не превышающих значения напряжения σs, определяемого элементом Сен-Венана. При напряжениях σ ≥ σs общая деформация определяется суммированием деформаций обеих частей структурной модели.
Определяющее соотношение для стабильного вязкопластического материала, характеризуемого такой моделью, в простейшем случае имеет вид (2). Понятие стабильного деформируемого материала означает в данном случае независимость его механических свойств от начала отсчета времени.
Применение структурной модели (2) деформируемого тела определяется правилом: если величина действующего в деформируемом теле σ(t) < σs, то используется только первое слагаемое соотношения (2), в противном случае – оба слагаемых.
Из структуры рассматриваемой модели видно, что напряжение, приложенное к первому обобщенному линейному элементу, равно сумме напряжений в параллельно соединенных втором обобщенном линейном элементе и элементе Сен-Венана. Поскольку общая деформация равна сумме деформаций последовательно соединенных частей модели, то есть ε = ε1 + ε2, то имеем, используя обозначения П*, П1* для операторов ползучести, R*, R1* – для соответствующих операторов релаксации и I – для единичного оператора:
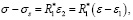 (3)
(3)
откуда получаем 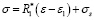 .
.
При учете равенства 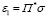 имеем
имеем
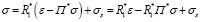 .
.
Отсюда следует
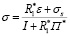 (4)
(4)
Совершенно аналогичным способом можно получить и альтернативное представление:
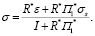 (5)
(5)
Нетрудно видеть, что эквивалентность соотношений (4) и (5) легко устанавливается при учете соотношений 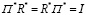 и
и 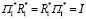 , умножая, к примеру, числитель и знаменатель правой части соотношения (3) на
, умножая, к примеру, числитель и знаменатель правой части соотношения (3) на 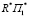 .
.
Естественное обобщение одномерной структурой модели деформируемого тела состоит в увеличении числа последовательно соединяемых звеньев:
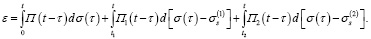 (6)
(6)
В этом варианте модели вводятся уже три функции ползучести, два предельных параметра по величине напряжения и два временных параметра, определяющих моменты включения соответствующего звена в число действующих.
Таким образом, при монотонном увеличении напряжения, начиная от нуля, на первой стадии учитывается только первое слагаемое в правой части соотношения (6). Может оказаться так, что при нагружении уровень напряжения, равный 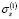 , достигнут не будет; в этом случае соотношение (6) будет описывать процесс линейного деформирования вязкоупругого материала при помощи наиболее общей линейной формы.
, достигнут не будет; в этом случае соотношение (6) будет описывать процесс линейного деформирования вязкоупругого материала при помощи наиболее общей линейной формы.
Допустим теперь, что при монотонном нагружении значение напряжения в некоторый момент времени t1 достигает значения 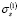 и превысит его, после чего второе звено структурной модели включается в число активных, что и отражается в значении нижнего предела интегрирования во втором интеграле правой части соотношения (6); обозначим этот период как вторую стадию процесса деформирования. Верхние пределы первого и второго интегралов в (6) есть текущее время процесса. Это означает, что общее значение деформации на второй стадии определяется как сумма первых двух слагаемых в (6).
и превысит его, после чего второе звено структурной модели включается в число активных, что и отражается в значении нижнего предела интегрирования во втором интеграле правой части соотношения (6); обозначим этот период как вторую стадию процесса деформирования. Верхние пределы первого и второго интегралов в (6) есть текущее время процесса. Это означает, что общее значение деформации на второй стадии определяется как сумма первых двух слагаемых в (6).
Точно так же после достижения в момент времени t2 действующим напряжением значения 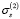 общая деформация определяется как сумма всех трех слагаемых в (6). На третьей стадии процесса деформирования, таким образом, в расчет принимаются вклады от всех трех слагаемых правой части соотношения (6).
общая деформация определяется как сумма всех трех слагаемых в (6). На третьей стадии процесса деформирования, таким образом, в расчет принимаются вклады от всех трех слагаемых правой части соотношения (6).
Дальнейшие обобщения в этом направлении проводятся по такому же алгоритму и затруднений не вызывают. Следует, однако, иметь в виду то, что суммировать указанным образом, строго говоря, можно только бесконечно малые деформации, поскольку конечные и большие деформации не являются адаптивными [12].
Если имеется набор из k диаграмм ползучести εk(t), удовлетворяющих условиям однородности и аддитивности, полученных в соответствии с законом изменения напряжений для заданных значений σ0k, функции линейной ползучести П(t) определяются при помощи соотношений
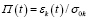 , k = 1, 2, …, (7)
, k = 1, 2, …, (7)
где σ0k – постоянное напряжение.
В общем случае минимально возможное число реализаций при проверке условий одномерности и аддитивности не может быть меньше трех.
В этих соотношениях используется точное значение параметра 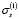 , которое также подлежит определению на этом этапе. С этой целью возьмем две реализации диаграмм ползучести, полученные при различных значениях действующего постоянного напряжения. Исходя из соотношений (6), имеем систему двух уравнений
, которое также подлежит определению на этом этапе. С этой целью возьмем две реализации диаграмм ползучести, полученные при различных значениях действующего постоянного напряжения. Исходя из соотношений (6), имеем систему двух уравнений
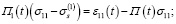 (8)
(8)
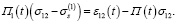 (9)
(9)
В качестве примера применения кусочно-линейных форм определяющих соотношений приведен анализ кривых ползучести мерзлого грунта – супеси, исследуемых в лаборатории механики мерзлых грунтов МГУ при испытаниях на одноосное сжатие при температуре T = -10 ºC.
Результаты исследования и их обсуждение
С помощью стандартных приемов обработки экспериментальной информации были определены абсолютные значения деформаций, применяемые с целью избежать использования знака минус в полученных данных, поскольку эксперименты проводились в условиях сжатия.
Кривые ползучести были получены при различных постоянных значениях напряжений в течение определенного периода времени, вплоть до 15 ч. Экспериментальные значения деформации приведены в табл. 1 для постоянных значений напряжений σ0 = 1; 2; 2.5; 3; 3.5; 4; 4.5; 5 (в МПа). Время приводится в минутах. Выбор моментов времени замеров показаний деформаций отражен в табл. 1.
Таблица 1
Экспериментальные значения деформаций при различных постоянных значениях напряжений
|
t, мин |
σ0 = 1МПа |
σ0 = 2МПа |
σ0 = 2,5МПа |
σ0 = 3МПа |
σ0 = 3,5МПа |
σ0 = 4МПа |
σ0 = 4,5МПа |
σ0 = 5МПа |
|
0 |
0,002 |
0,0058 |
0,0149 |
0,027 |
0,041 |
0,047 |
0,060 |
0,075 |
|
25 |
0,0028 |
0,0071 |
0,0172 |
0,0355 |
0,052 |
0,068 |
0,073 |
0,145 |
|
50 |
0,0032 |
0,0078 |
0,0186 |
0,0405 |
0,059 |
0,084 |
0,120 |
0,240 |
|
75 |
0,0036 |
0,0086 |
0,020 |
0,0455 |
0,065 |
0,099 |
0,155 |
|
|
100 |
0,004 |
0,0093 |
0,0212 |
0,049 |
0,069 |
0,0112 |
0,185 |
|
|
150 |
0,0044 |
0,0108 |
0,0232 |
0,054 |
0,076 |
0,133 |
||
|
200 |
0,0048 |
0,0119 |
0,025 |
0,058 |
0,081 |
0,151 |
||
|
250 |
0,0051 |
0,0129 |
0,0265 |
0,060 |
0,085 |
0,169 |
||
|
300 |
0,0055 |
0,0135 |
0,028 |
0,063 |
0,070 |
0,20 |
||
|
400 |
0,0062 |
0,0145 |
0,030 |
0,067 |
0,095 |
|||
|
500 |
0,007 |
0,016 |
0,032 |
0,070 |
0,110 |
|||
|
600 |
0,0075 |
0,0175 |
0,034 |
0,073 |
0,123 |
|||
|
700 |
0,008 |
0,0185 |
0,0355 |
0,076 |
0,140 |
|||
|
800 |
0,0085 |
0,0195 |
0,037 |
0,079 |
0,169 |
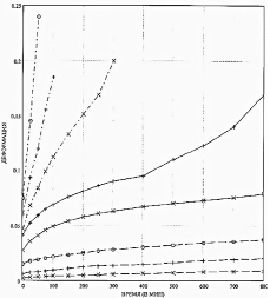
Рис. 1. Кривые ползучести при заданных значениях постоянного напряжения Условные обозначения: (---х) – 1 МПа; (---+) – 2 МПа; (---о) – 2,5 МПа; (___х) – 3 МПа; (___+) – 3,5 МПа; (-.-.-х) – 4 МПа; (-.-.-+) – 4,5 МПа; (-.-.-о) – 5 МПа
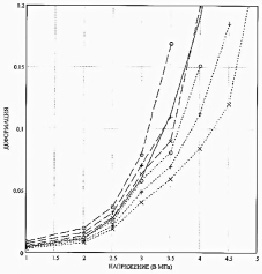
Рис. 2. Изохронные кривые ползучести Условные обозначения: (…х) – 50 мин;(….+) – 100 мин; (…о) – 200 мин; (---х) – 300 мин; (---+) – 500 мин; (---о) – 800 мин; (___) – ε=0.0041+0.0069* (σ-1)3, σ в МПа
Приведенные в табл. 1 экспериментальные значения представлены тоже в виде графиков на рис. 1. Кривые ползучести располагаются здесь в порядке возрастания перечисленных выше значений постоянного напряжения снизу вверх: первые три столбца со значениями деформаций из табл. 1 приведены в виде штриховых линий, вторые два – сплошными линиями и последние три – штрихпунктирными линиями.
Определенный интерес при анализе экспериментальных кривых ползучести представляет построение изохронных кривых, то есть зависимостей значений деформаций от напряжений при некотором фиксированном значении времени. Такие кривые приведены на рис. 2. Здесь по оси абсцисс заданы напряжения, а по оси ординат – деформации. В качестве базовых выбраны следующие значения времени: 50, 100, 200, 300, 500, 800 мин.
Видно, что в основной части изменения параметров такие кривые удовлетворительно аппроксимируются функцией вида 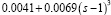 . Она приведена в виде сплошной кривой на рис. 2. Обратим внимание на то, что при значении напряжения σ0 = 3.5 МПа изохронные кривые располагаются значительно ниже приведенной здесь кубической параболы.
. Она приведена в виде сплошной кривой на рис. 2. Обратим внимание на то, что при значении напряжения σ0 = 3.5 МПа изохронные кривые располагаются значительно ниже приведенной здесь кубической параболы.
Наблюдаемое противоречие состоит в том, что приращение деформаций при переходе от σ0 = 3 МПа к σ0 = 3.5 МПа меньше, чем при переходе от σ0 = 2.5 МПа к σ0 = 3 МПа. Нетрудно убедиться, на примере перехода от σ0 = 3.5 МПа к σ0 = 4 МПа, в справедливости такого заключения.
Непосредственно из второго и третьего столбцов табл. 1 видно, что при увеличении напряжения вдвое деформации возрастают в большей степени. Это означает нарушение принципа однородности, в силу чего граница, разделяющая линейную и нелинейную области поведения материала, располагается ниже значения σ0 = 2 МПа. Вместе с тем наблюдаемое отклонение незначительно, что позволяет предположить, что при σ0 = 1 МПа поведение грунта линейное.
Воспользовавшись таким предположением, находим функцию линейной ползучести П(t), значения которой в заданные моменты времени приведены в третьем столбце табл. 2. График функций линейной ползучести приведен также на рис. 3 в виде сплошной линии с нанесенными на ней кружками, положение которых определяется значениями третьего столбца табл. 2. Пунктирной линией, практически совпадающей с указанной кривой, дается график приближенной аналитической зависимости для функции линейной ползучести
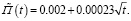 (10)
(10)
Реализуя далее вычислительную процедуру в соответствии с соотношениями (3)–(5), находим параметр 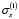 и функцию ползучести П1(t) для фиксированных моментов времени, указанных во втором столбце табл. 2.
и функцию ползучести П1(t) для фиксированных моментов времени, указанных во втором столбце табл. 2.
Таблица 2
Параметры функции линейной ползучести
|
NN п/п |
t, мин |
П(t), 1/МПа |
|
П1(t), 1/МПа |
|
П2(t), 1/МПа |
|
1 |
0 |
0,002 |
1,89 |
0,016 |
2,65 |
0,013 |
|
2 |
25 |
0,0028 |
1,91 |
0,017 |
2,65 |
0,023 |
|
3 |
50 |
0,0032 |
1,92 |
0,018 |
2,65 |
0,029 |
|
4 |
75 |
0,0036 |
1,93 |
0,019 |
2,65 |
0,033 |
|
5 |
100 |
0,004 |
1,93 |
0,020 |
2,65 |
0,037 |
|
6 |
150 |
0,0044 |
1,90 |
0,021 |
2,65 |
0,043 |
|
7 |
200 |
0,0048 |
1,89 |
0,022 |
2,65 |
0,048 |
|
8 |
250 |
0,0051 |
1,88 |
0,023 |
2,65 |
0,0515 |
|
9 |
300 |
0,055 |
1,89 |
0,024 |
2,65 |
0,0545 |
|
10 |
400 |
0,062 |
1,92 |
0,025 |
2,65 |
0,060 |
|
11 |
500 |
0,07 |
1,92 |
0,026 |
2,65 |
0,0645 |
|
12 |
600 |
0,0075 |
1,88 |
0,0265 |
2,65 |
0,069 |
|
13 |
700 |
0,008 |
1,90 |
0,027 |
2,65 |
0,073 |
|
14 |
800 |
0,0085 |
1,91 |
0,0275 |
2,65 |
0,077 |
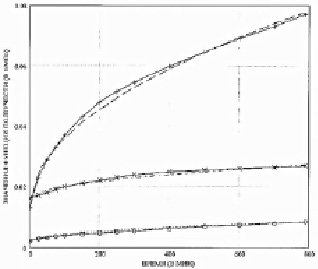
Рис. 3. Функции ползучести. Условные обозначения: (___0) – функция линейной ползучести П(t); (…..) – ее аппроксимация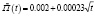 ; (___х) – первая линейная функция ползучести П1(t); (-.-.-) – ее аппроксимация
; (___х) – первая линейная функция ползучести П1(t); (-.-.-) – ее аппроксимация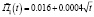 ; (___+) – вторая линейная функция ползучести П2(t); (---) ее аппроксимация
; (___+) – вторая линейная функция ползучести П2(t); (---) ее аппроксимация 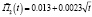
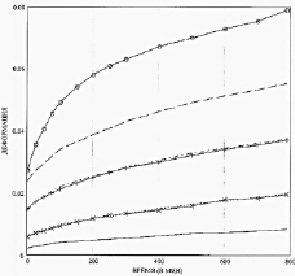
Рис. 4. Экспериментальные и расчетные кривые ползучести при заданных значениях постоянного напряжения. Условные обозначения: (___) – эксперимент, 1 МПа; (___х) – эксперимент, 2 МПа; (……) – расчет, 2 МПа; (___+) – эксперимент, 2,5 МПа; (-.-.-) – расчет, 2.5 МПа; (____о) – эксперимент, 3 МПа; (---) – расчет, 3 МПа
Здесь же в четвертой и пятой колонках приведены расчетные значения этих величин. Исходя из расчетных значений принимаем 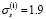 МПа. График первой линейной функции ползучести П1(t) приведен на рис. 3 в виде сплошной линии с нанесенными в соответствии с данными табл. 2 крестиками. Здесь же штрихпунктирной линией представлен график аппроксимирующей ее функции:
МПа. График первой линейной функции ползучести П1(t) приведен на рис. 3 в виде сплошной линии с нанесенными в соответствии с данными табл. 2 крестиками. Здесь же штрихпунктирной линией представлен график аппроксимирующей ее функции:
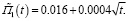 (11)
(11)
Возможность применения полученных выше параметров иллюстрируется данными на рис. 4. Здесь сплошными линиями с нанесенными крестиками, плюсиками и кружками приведены исходные кривые ползучести, полученные при σ0 = 2; 2.5; 3 МПа соответственно. Пунктирная, штрихпунктирная и штриховая линии получены расчетным путем с использованием полученных выше характеристик, при помощи соотношения
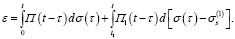 (12)
(12)
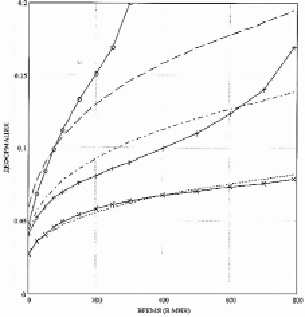
Рис. 5. Экспериментальные и расчетные кривые ползучести при заданных значениях постоянного напряжения. Условные обозначения: (___х) – эксперимент, 3 МПа; (……) – расчет, 3МПа; (___+) – эксперимент, 3,5 МПа; (-.-.-) – расчет, 3,5 МПа; (___о) – эксперимент, 4 МПа; (---) – расчет, 4 МПа
На рис. 4 для сравнения в виде сплошной линии приведена кривая ползучести, полученная при σ0 = 1 МПа.
Видно, что расчетные кривые ползучести удовлетворительно совпадают с соответствующими кривыми ползучести при σ0 = 2 МПа и σ0 = 2.5 МПа и в то же время непригодны для описания поведения деформируемого материала при σ0 = 3 МПа.
Очевидно, эта проблема легко решается введением в структурную модель деформируемого грунта дополнительного звена в соответствии с рассмотренным подходом. К сожелению, решение этой проблемы усложнилось в нашем случае в силу отмеченного выше «нелогичного» поведения кривой ползучести, полученной при σ0 = 3.5 МПа, приводящего к существенному разбросу расчетного значения параметра 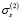 . Тем не менее методом подбора удалось найти среднее значение параметра
. Тем не менее методом подбора удалось найти среднее значение параметра 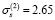 МПа и вычислить вторую линейную функции ползучести П2(t). Эти характеристики для указанных фиксированных моментов времени приведены в шестом и седьмом столбцах табл. 2. График П2(t) приведен в виде сплошной кривой с нанесенными на нее знаками «плюс». Точно так же, как и выше, приведем аналитическое выражение аппроксимирующей ее функции:
МПа и вычислить вторую линейную функции ползучести П2(t). Эти характеристики для указанных фиксированных моментов времени приведены в шестом и седьмом столбцах табл. 2. График П2(t) приведен в виде сплошной кривой с нанесенными на нее знаками «плюс». Точно так же, как и выше, приведем аналитическое выражение аппроксимирующей ее функции:
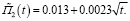 (13)
(13)
Ее график представлен штриховой линией на рис. 3.
Результаты расчетов кривых ползучести при помощи трехчленной структурной формы определяющего соотношения приведены на рис. 5. Здесь сплошные линии, отмеченные крестиками, плюсиками и кружками, представляют собой экспериментально определенные кривые ползучести, полученные при σ0 = 3; 3.5;4 МПа соответственно. Кривые ползучести, определяемые расчетным путем, приведены в виде пунктирных, штрихпунктирных и штриховых линий соответственно.
Выводы
1. Предложена методика анализа кривых ползучести при испытаниях мерзлых и оттаивающих грунтов методами сжатия на основе кусочно-линейной аппроксимации.
2. Полученные при анализе кривых ползучести закономерности согласуются с классическими и современными представлениями о реологическом поведении мерзлого и оттаивающего грунтов под нагрузками.
3. Обработка данных экспериментальных исследований поведения кривых ползучести по данной методике позволяет прогнозировать деформирование мерзлого и оттаивающего грунтов на срок службы инженерного сооружения при изменении природных и техногенных условий.
Библиографическая ссылка
Царапов М.Н. МЕТОДИКА АНАЛИЗА КРИВЫХ ПОЛЗУЧЕСТИ МЕРЗЛЫХ И ОТТАИВАЮЩИХ ГРУНТОВ НА ОСНОВЕ МЕТОДА КУСОЧНО-ЛИНЕЙНОЙ АППРОКСИМАЦИИ // Успехи современного естествознания. 2024. № 12. С. 84-92;URL: https://natural-sciences.ru/ru/article/view?id=38353 (дата обращения: 13.03.2026).
DOI: https://doi.org/10.17513/use.38353




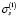 , МПа
, МПа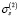 , МПа
, МПа