Научный журнал

Успехи современного естествознания

ISSN 1681-7494

"Перечень" ВАК

ИФ РИНЦ = 0,775

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Половнев О.В. 1 Гафаар А. 1

---

1 ФГБОУ ВО «Московский государственный университет геодезии и картографии»

Цель данного исследования – моделирование проекта по сгущению координатной основы на территории Сирийской Арабской Республики, алгоритм проведения априорной оценки точности плановой геодезической сети страны и анализ результатов моделирования. Для достижения цели исследования применены программы Leica_GEO_Office, Excel, MATHCAD, Civil 3D. Точность спроектированной модели геодезической сети была оценена с использованием метода наименьших квадратов. В результате теоретического и практического исследования была смоделирована геодезическая сеть, выполнена априорная оценка точности планируемой геодезической сети. Сеть предполагается создавать спутниковым методом. Основываясь на результатах предварительного анализа, различные варианты проектирования геодезической сети могут быть сформированы в процессе оптимизации с использованием моделирования, после чего выбирается вариант, который наилучшим образом соответствует требованиям. Для получения наилучших результатов по точности смоделированной сети, необходимо определить местоположение для каждого нового пункта и определить, как он влияет на точность сети. Существующая в Сирии геодезическая сеть не способна удовлетворить нужды национальной экономики и не соответствует современным стандартам по точности и плотности размещения точек. Это показывает важность данного исследования в будущем для восстановления страны после окончания войны.

Статья в формате PDF

612 KB

стереографическая проекция

геодезическая система координат

метод наименьших квадратов

математическое моделирование

пункты геодезической сети

1. Мусбах Асаад Али. Современное состояние геодезической сети на территории Сирийской Арабской Республики // Геодезия и аэрофотосъемка. 2011. № 3. С. 13–15. ‏

2. Habib M. Fit-for-purpose conformal mapping for sustainable land administration in war-ravaged Syria // Heliyon. 2022. Vol. 8. DOI: 10.1016/j.heliyon.2022.e09384.

3. Кутени Джад Аль Карим Хамад. Разработка методики геодезического обеспечения исследования деформации при нефтедобыче на территории Сирийской Арабской Республики: автореф. дис. … канд. техн. наук. Москва, 2020. 24 с.

4. Коссугбето Бриак Кевин Патрик. Совершенствование координатной основы на территории республики Бенин: автореф. дис.… канд. техн. наук. Москва, 2015. 24 с.

5. Мустафин М.Г. Обоснование технологии создания спутниковой геодезической сети для условий низких широт: автореф. дис … канд. техн. наук. Санкт-Петербург, 2018. 24 с.

6. Абаас Гафаар. Особенности вычисления параметров трансформирования из WGS84 в Кларк 1880 в горных и пустынных районах в сирийской стереографической проекции // Успехи современного естествознания. 2022. № 8. С. 145–149. DOI: 10.17513/use.37881.

7. Абаас Гафаар. Особенности вычисления параметров трансформирования и уравнения регрессии из WGS84 в Кларк1880 в сирийской системе координат Ламберта // Успехи современного естествознания. 2022. № 9. С. 92–98. DOI: 10.17513/use.37898.

8. Мустафин М.Г., Грищенкова Е.Н., Юнес Ж.А., Худяков Г.И. Современное маркшейдерско-геодезическое обеспечение эксплуатации горных предприятий // Известия Тульского государственного университета. 2017. № 4. С. 190–203.

Введение

В настоящее время на территории Сирийской Арабской Республики (САР) геодезическая сеть включает в себя несколько частей, созданных в разные периоды, и не соответствует современным стандартам, поскольку не обновлялась в последние годы с использованием современных технологий. В результате военных действий страна потеряла значительное количество геодезических пунктов, и сеть либо не развивалась вовсе, либо ее развитие происходило только на небольших участках территории. Также в стране отсутствуют высокоточное нивелирование и гравиметрические сети. Поэтому возникает необходимость создать единую государственную геодезическую сеть по всей территории страны [1–3].

Проектирование и строительство сел, городов, железных и шоссейных дорог, объектов инфраструктуры нельзя выполнять без качественной геодезической основы. Чтобы исправить недостатки действующих геодезических сетей, усовершенствовать основу и внедрить единую координатную систему в стране, необходима как реставрация уже имеющихся сетей, так и создание новых. Метод спутниковых технологий на данный момент является наиболее оптимальным вариантом для создания геодезических сетей [4].

Цель данного исследования – моделирование проекта по сгущению координатной основы на территории САР, алгоритм проведения априорной оценки точности плановой геодезической сети страны и анализ результатов моделирования.

Материалы и методы исследования

В данной работе использованы характеристики современных геодезических приборов (Leica GS14 3.75G, где точность измерения составляет 5 мм + 0,5 ppm), компьютерные технологии (Leica_GEO_Office, Excel, MATHCAD, Civil 3D), связанные с разработкой алгоритмов и моделированием, информация о картографических проекциях, применяемых на исследуемых территориях.

Применены методы и подходы, связанные с теорией математической обработки геодезических данных, включая метод наименьших квадратов, аспекты аналитической геометрии, создание моделей геодезических сетей, как на плоскости, так и в трехмерном пространстве, а также методологии математической статистики.

Результаты исследования и их обсуждение

Для сгущения геодезической сети авторы собрали информацию о геодезических и местных координатах опорных геодезических пунктов, проанализировав картографическую основу САР с расположением всех основных дорог, озер, рек и т.д., и по результатам анализа были выбраны местоположения новых пунктов с учетом следующих критериев [4, 5]:

‒ расстояние между проектируемыми пунктами не должно было превышать 20 км;

‒ при моделировании учитывалось расположение труднодоступных мест, водохранилищ и дорог;

‒ проект осуществлялся в стереографической системе координат, которая считается наиболее эффективной в САР. В дальнейшем в этой системе будут осуществляться все топографические работы.

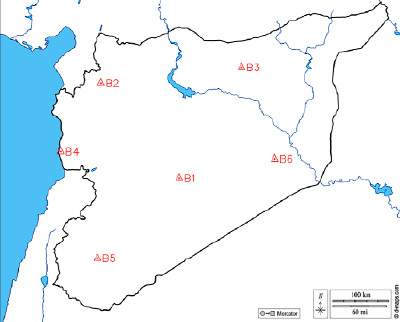
Рис. 1. Смоделированная геодезическая сеть высшего класса точности Источник: составлено авторами)

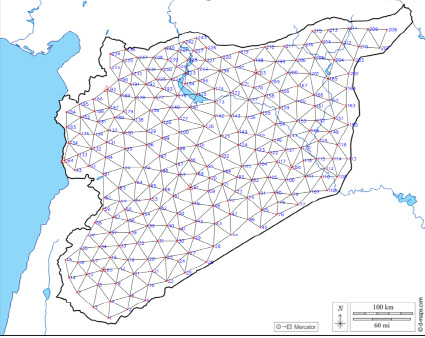
Рис. 2. Схема проектируемой сети на территории САР (составлено авторами)

С помощью программы Civil 3D был смоделирован проект высшего класса, представленный на рис. 1 и включающий в себя шесть опорных точек (В1–В6). Авторы зафиксировали координаты и смоделировали 243 геодезических пункта (1–243) в соответствии с заданными условиями. Схема сети показана на рис. 2.

Алгоритм выполнения априорной оценки точности плановой геодезической сети на территории САР

Для достижения оптимального результата в создании геодезических сетей важно провести оценку точности сети как в процессе проектирования, так и после ее построения. Предварительная оценка точности геодезической сети обеспечивает решение многих задач, например определение наилучшего варианта создания сети, экономию времени, усилий и денег, определение точности используемых приборов и методов измерений [5, 6].

В настоящее время, используя современные компьютеры и с помощью метода наименьших квадратов, проводится оценка точности созданной сети, а также определяется наиболее подходящее размещение точек. Точность будет оцениваться согласно известной формуле

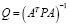, (1)

где Р – матрица весов измеренных величин; A – матрица частных производных уравнений поправок; Q – матрица весовых коэффициентов определяемых пунктов.

Средняя квадратическая погрешность положения каждого пункта в сети может быть определена по формуле

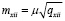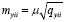, , (2)

где μ – ошибка единицы веса; qxii, qyii – соответствующие диагональные элементы матрицы Qx, Qy.

Предварительный анализ точности установления предполагаемого расположения точек спутниковой сети в отношении исходных пунктов можно выполнить, строго применяя параметрический метод уравнивания.

Погрешности положения пунктов вычисляются следующими действиями с помощью программных комплексов Excel и MATHCAD [7, 8]:

‒ выполнить преобразование всех данных в сирийской стереографической проекции, применяя параметры преобразования [6, 7];

‒ вычислить «истинные» приращения координат

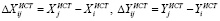; (3)

‒ вычислить «измеренные» приращения координат

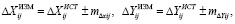(4)

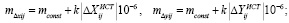где (5)

‒ вычислить «приближенные» координаты определяемых пунктов

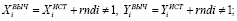(6)

‒ сформировать «приближенные» приращения координат

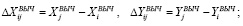(7)

‒ сформировать свободные члены (невязки)

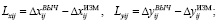(8)

‒ сформировать вес измеренных величин

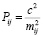, (9)

где с = 10

‒ составить систему нормальных уравнений

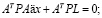(10)

фрагмент матрицы А выглядит следующим образом:

(11)

Выполнить уравнивание геодезической сети

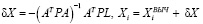(12)

и определить точность координат пунктов

, , ,

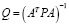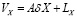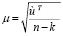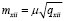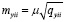, , (13)

,

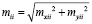где μ – средняя квадратическая погрешность единицы веса; mii – средние квадратические погрешности определения пунктов спутниковой сети.

Создавая алгоритм выбора оптимального положения пунктов через уравнивание геодезической сети с частичным смещением пунктов (от нескольких сотен метров до единиц километров), определяли наилучшее по точности положение пункта с одновременной фиксацией обновленной конфигурации смоделированной геодезической сети.

Основываясь на результатах анализа, среднее значение ошибок составило 2,6 см, и в северо-восточной части страны оно достигает 6 см. На рис. 3 и 4 для наглядности демонстрируются средние квадратные ошибки расположения точек относительно координатных осей X и Y, а в табл. 1 и 2 даны пояснения и соотношения цветовых гамм в достижимой точности.

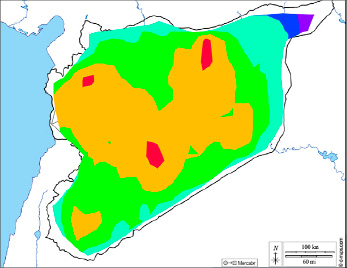
Рис. 3. Распределение средних квадратических погрешностей по оси X Источник: составлено авторами

Таблица 1

Цветовая градация средних квадратических погрешностей по оси Х

Создавая алгоритм смещения пунктов (от нескольких сотен метров до единиц километров) и проводя уравнивание, авторы определили наилучшую по точности конфигурацию смоделированной геодезической сети.

В рассмотренном случае смещение производилось вручную сменой координат пунктов по заданной схеме, для автоматизации алгоритма целесообразно перейти от Excel и MATHCAD к программным комплексам, которые позволят это сделать автоматически.

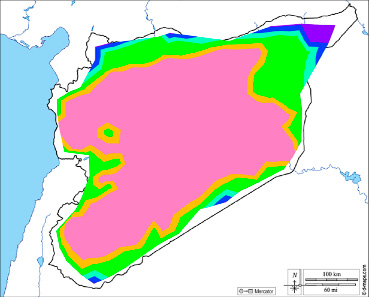
Рис. 4. Распределение средних квадратических погрешностей по оси Y Источник: составлено авторами

Таблица 2

Цветовая градация средних квадратических погрешностей по оси Y

Заключение

На территории САР была смоделирована геодезическая сеть, которая покрывает равномерно всю территорию страны. Выполнена априорная оценка точности проектируемой геодезической сети. Достигнутые точности моделирования позволяют утверждать, что такие сети могут быть созданы с помощью оборудования Leica GS14 3.75G, где точность измерения составляет [5 мм + 0,5 ppm] при заранее определенных условиях. Применение алгоритмической схемы выбора оптимального положения пунктов позволяет выбрать наилучшую конфигурацию геодезической сети в зависимости от заданных параметров оптимизации. Для автоматизации описанного процесса рекомендуется использовать профессиональные программные комплексы.

Библиографическая ссылка