Введение
В настоящее время широко распространено применение спутниковых технологий для решения геодезических задач. Одним из основных аргументов при выборе вышеуказанной технологии является экономия времени и трудозатрат. Наиболее популярным режимом измерений спутниковым оборудованием является кинематика в реальном времени (далее – RTK). Реализация такого метода предполагает непрерывную связь со спутниковой группировкой, базовой станцией и ровером [1]. Ключевые преимущества RTK над другими режимами:
– использование дифференциальных поправок от базовых станций, что, в свою очередь, позволяет компенсировать влияние атмосферы при определении псевдодальности [2];
– возможность получения координат искомой точки в режиме реального времени;
– отсутствие необходимости во втором комплекте спутникового оборудования, так как пользователь имеет возможность получить поправки от сетей базовых станций, доступ к которым предоставляется провайдерами таких сетей;
– приемлемая точность для большинства геодезических работ [3, 4].
Несмотря на вышеуказанные преимущества, режим RTK имеет ограничение в предельном расстоянии от базовой станции до 30 км [5]. Следует упомянуть о снижении точности определения координат при увеличении расстояния до базовой станции. В качестве примера рассмотрим приемник EFT M4 GNSS [6]. Его априорная средняя квадратическая погрешность (далее – СКП) в плане имеет следующие характеристики: ±5 мм +0,5 мм/км. Из чего следует, что на условном нулевом километре от базовой станции точку можно определить с точностью в 5 мм, на 10-м километре – 10 мм и на 20-м – 15 мм соответственно [3]. Частично такое положение дел складывается из-за того, что ионосфера и тропосфера неоднородны по своей природе, а задержки прохождения сигнала через эти сферы вносят ключевой вклад в ухудшение точности получения координат спутниковым методом [7]. Технология виртуальных базовых станций (далее – VRS) призвана скомпенсировать вышеизложенные ошибки. Реализуется она по следующему принципу:
– при инициализации приемники пользователя отправляют свое примерное местоположение сети базовых станций;
– сеть, анализируя местонахождение пользователя, передает усредненную корректирующую информацию от ближайших базовых станций;
– сеть программно создает виртуальную базовую станцию (далее – bVRS) вблизи пользователя (на расстояние 10–15 м) и генерирует набор виртуальных измерений [8, 9].
Не возникает сомнения, что технология VRS должна повысить точность определения координат спутниковым методом, так как в том числе возникает фактор избыточных измерений [10]. Но неясно, на какую величину она улучшится. Возвращаясь к априорной СКП в плане спутникового оборудования ±5 мм +0,5 мм/км, очевиден следующий тезис. Так как bVRS генерируется в непосредственной близости от пользователя, то априорная СКП будет ±5 мм +0,5 мм, то есть 5 мм. Но при таком подходе не учитывается, с какой точностью в плановом положении была сгенерирована виртуальная станция. В свою очередь, оценить точность bVRS прямыми измерениями не представляется возможным.
В целом априорная СКП, указанная в технических характеристиках спутникового оборудования, говорит о том, что оборудования способно определить координаты с указанной точностью после холодного старта. Что, в свою очередь, не отображает точностные характеристики взаимного расположения определяемых пунктов в рамках одного цикла измерений. В качестве примера предположим, что после инициализации спутникового оборудования было определено плановое положение нескольких точек. Точность определения координат этих точек должна быть приближена к априорной СКП, но точность определения взаимного расположения точек относительно друг друга остается нераскрытой.
Для упрощения восприятия нижеизложенного текста введем ряд определений.
Холодная погрешность – это погрешность определения координат после инициализации оборудования, предположительно может быть систематической для ряда определений координат в рамках одного цикла измерений.
Относительная погрешность – это погрешность определения приращений координат между наблюдаемыми точками и/или базисов образуемых между точками, предположительно может быть независима от холодной погрешности.
Цель исследования – определить фактическую среднюю квадратическую погрешность координат виртуальной станции как следствие, уточнить СКП спутникового оборудования при использовании технологии VRS. Определить холодную и относительную погрешности для режима измерений в RTK и для режима измерений RTK с использованием технологии VRS.
Материалы и методы исследования
Исследование точности кинематики в реальном времени проводилось на двух объектах:
– ЖК «Квартал Герцена», расположенный по адресу: г. Москва, Бирюлево Восточное, 25–26 км МКАД;
– комплексная жилая застройка по адресу: Московская область, городской округ Балашиха, квартал «Б» (далее квартал – «Б»).
В качестве спутникового оборудования был использован приемник EPOCH 35, априорная СКП в плане в режиме RTK равна ±10 мм +1 мм/км, базовая станция находилась на удалении примерно 4 км, за исключением серий измерений от 29.05.2025.
Исследования точности кинематики в реальном времени с использованием виртуальной базовой станции делились на полевые и камеральные работы.
Полевые работы заключались в нижеизложенном:
– цикл наблюдения представлял собой определение плановых координат в режиме RTK и/или в режиме VRS, в рамках одного цикла координаты определялись для трех жестко закрепленных на местности точек;
– измерение расстояний между точками при помощи тахеометра;
– в рамках одного рабочего дня проводилось не менее трех циклов наблюдений.
Камеральная обработка данных заключалась в определении фактической СКП для двух режимов наблюдений [11]. Определение отклонений базисов (расстояний) между координатами точек, полученных с помощью спутникового оборудования, по отношению к линейным размерам, полученным с помощью электронного тахеометра.
Результаты исследования и их обсуждение
Есть вероятность того, что относительная погрешность координатных определений может быть свободна или частично ослаблена от влияния тропосферы, так как наблюдения проводятся в относительно близком временном промежутке и тропосфера остается относительно неизменной. Наиболее репрезентативно, по мнению автора, будет проанализировать длину базисов между точками, полученными с помощью спутниковых определений.
Рассмотрим два варианта вычисления СКП базисов: по формуле Гаусса и по формуле Бесселя.
Таблица 1
Определение СКП базисов в режиме RTK по формулам Гаусса и Бесселя
|
01.09.24 ЖК «Квартал Герцена» |
|||||
|
Направление базисов |
Отклонение базисов от эталона |
СКП (RTK) по ф-ле Бесселя |
СКП (RTK) по ф-ле Гаусса |
||
|
Цикл 1 (RTK) |
Цикл 2 (RTK) |
Цикл 3 (RTK) |
|||
|
Т1-Т2 |
0,002 |
-0,026 |
0,010 |
0,019 |
0,016 |
|
Т2-Т3 |
-0,015 |
-0,001 |
0,010 |
0,013 |
0,010 |
|
Т3-Т1 |
-0,030 |
0,009 |
0,018 |
0,026 |
0,021 |
|
22.09.24 ЖК «Квартал Герцена» |
|||||
|
Т1-Т2 |
-0,012 |
-0,033 |
-0,006 |
0,014 |
0,021 |
|
Т2-Т3 |
-0,019 |
-0,024 |
0,025 |
0,027 |
0,023 |
|
Т3-Т1 |
-0,007 |
-0,003 |
-0,002 |
0,003 |
0,005 |
|
03.11.24 ЖК «Квартал Герцена» |
|||||
|
Т1-Т2 |
-0,003 |
-0,013 |
0,005 |
0,009 |
0,008 |
|
Т2-Т3 |
-0,014 |
-0,025 |
-0,006 |
0,010 |
0,017 |
|
Т3-Т1 |
-0,020 |
-0,031 |
0,000 |
0,016 |
0,021 |
|
26.07.25 ЖК «Квартал Герцена» |
|||||
|
Т1-Т2 |
0,011 |
-0,005 |
0,010 |
0,009 |
0,009 |
|
Т2-Т3 |
0,011 |
0,004 |
-0,003 |
0,007 |
0,007 |
|
Т3-Т1 |
0,007 |
-0,026 |
0,002 |
0,012 |
0,016 |
|
09.08.25 ЖК «Квартал Герцена» |
|||||
|
Т1-Т2 |
0,025 |
0,023 |
0,001 |
0,013 |
0,020 |
|
Т2-Т3 |
0,018 |
0,001 |
-0,003 |
0,011 |
0,011 |
|
Т3-Т1 |
0,014 |
-0,001 |
0,009 |
0,008 |
0,010 |
Источник: составлено автором на основе полученных данных в ходе исследования.
В первом варианте в качестве известной величины базисов будут использованы данные, полученные с помощью тахеометра. Для данного способа СКП определения базисов будет равна
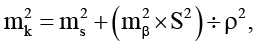
где mк = 2 мм, где
ms – погрешность измерения расстояния = ±2 мм;
mβ – погрешность измерения угла =1";
S – измеренное расстояние в мм
(≈ 30 м = 30000 мм);
ρ – (радиан) =206265" (секунд);
так как определение базиса между двумя точками определяется путем определения координат двух точек, то максимальная погрешность измерения mу будет равна: 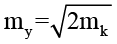 ; mу = 3 мм.
; mу = 3 мм.
Следует отметить, что при благоприятных (фактических лабораторных) условиях точность определения базисов, полученных с помощью спутникового оборудования, не менее 10 мм. Точность определения базисов тахеометров – 3 мм. Исходя из вышеизложенного, было принято решение пренебречь погрешностью тахеометра и принять данные базисов, полученных им, за истинные.
Всего было выполнено 5 серий измерений в режиме RTK и 3 серии измерений в режиме VRS. Результаты определения СКП базисов в режиме RTK приведены в табл. 1, результаты определения СКП базисов в режиме VRS – в табл. 2.
Исходя из вышеизложенных таблиц, можно сделать выводы.
1. В режиме РТК максимальное СКП по формуле Бесселя – 27 мм и по формуле Гаусса – 23 мм, минимальное СКП – 3 мм и 5 мм соответственно. В свою очередь, отечественные коллеги проводили похожее исследования, результат определения базисов находился в диапазоне от 4 до 32 мм, что является сопоставимыми величинами с данными, указанными выше [12].
2. В режиме VRS максимальное СКП по формуле Бесселя – 11 мм и по формуле Гаусса – 9 мм, минимальное СКП 2 и 4 мм соответственно.
Максимальное СКП в обоих режимах измерений было получено в рамках одной серии наблюдений от 27.05.25.
Также был проведен анализ СКП определения плановых координат в двух режимах измерений. С результатами можно ознакомиться в табл. 3 и 4.
В режиме RTK СКП определения плановых координат находится в диапазоне от 1 до 17 мм, при наличии скачков – до 23 мм.
Следует отметить, что отечественные авторы в своей работе «Применение ГНСС в прикладной геоинформатике» проводили исследования в области определения сходимости плановых координат, полученных с помощью спутникового оборудования. При полевой части исследования использовалась базовая станция, находящаяся на расстоянии приблизительно 2 км, и передвижной приемник, закрепленный на автомобиле, движущемся со скоростью 3–5 км/ч. Результаты отечественных коллег свидетельствуют о сходимости плановых координат с точностью до 10 мм с разовыми скачками до 35 мм [13].
Таблица 2
Определение СКП базисов в режиме VRS по формулам Гаусса и Бесселя
|
22.09.24 ЖК «Квартал Герцена» |
|||||
|
Направление базисов |
Отклонение базисов от эталона |
СКП (VRS) по ф-ле Бесселя |
СКП (VRS) по ф-ле Гаусса |
||
|
Цикл 1 (VRS) |
Цикл 2 (VRS) |
Цикл 3 (VRS) |
|||
|
Т1-Т2 |
0,000 |
-0,003 |
0,006 |
0,005 |
0,004 |
|
Т2-Т3 |
0,010 |
0,002 |
0,012 |
0,005 |
0,009 |
|
Т3-Т1 |
0,010 |
0,005 |
-0,003 |
0,007 |
0,007 |
|
26.07.25 ЖК «Квартал Герцена» |
|||||
|
Т1-Т2 |
0,002 |
-0,009 |
0,000 |
0,006 |
0,005 |
|
Т2-Т3 |
0,007 |
0,003 |
0,006 |
0,002 |
0,006 |
|
Т3-Т1 |
0,004 |
-0,008 |
-0,010 |
0,008 |
0,008 |
|
09.08.25 ЖК «Квартал Герцена» |
|||||
|
Т1-Т2 |
0,001 |
-0,005 |
0,007 |
0,006 |
0,005 |
|
Т2-Т3 |
0,001 |
0,007 |
-0,014 |
0,011 |
0,009 |
|
Т3-Т1 |
0,011 |
0,005 |
-0,007 |
0,009 |
0,008 |
Источник: составлено автором на основе полученных данных в ходе исследования.
Таблица 3
СКП определения плановых координат в режиме RTK по формуле Бесселя
|
01.09.24 ЖК «Квартал Герцена» |
22.09.24 ЖК «Квартал Герцена» |
03.11.24 ЖК «Квартал Герцена» |
||
|
№ точки |
Ось |
СКП |
СКП |
СКП |
|
1 |
X |
0,016 |
0,001 |
0,004 |
|
Y |
0,014 |
0,015 |
0,017 |
|
|
2 |
X |
0,006 |
0,023 |
0,005 |
|
Y |
0,013 |
0,013 |
0,011 |
|
|
3 |
X |
0,007 |
0,011 |
0,009 |
|
Y |
0,018 |
0,006 |
0,019 |
|
|
26.07.25 ЖК «Квартал Герцена» |
09.08.25 ЖК «Квартал Герцена» |
|||
|
№ точки |
СКП |
СКП |
СКП |
|
|
1 |
0,003 |
0,006 |
0,006 |
|
|
0,006 |
0,006 |
0,006 |
||
|
2 |
0,009 |
0,006 |
0,006 |
|
|
0,013 |
0,003 |
0,003 |
||
|
3 |
0,003 |
0,017 |
0,017 |
|
|
0,004 |
0,006 |
0,006 |
||
Источник: составлено автором на основе полученных данных в ходе исследования.
Таблица 4
СКП определения плановых координат в режиме VRS по формуле Бесселя
|
22.09.24 ЖК «Квартал Герцена» |
26.07.25 ЖК «Квартал Герцена» |
09.08.25 ЖК «Квартал Герцена» |
||
|
№ точки |
Ось |
СКП |
СКП |
СКП |
|
1 |
X |
0,013 |
0,006 |
0,003 |
|
Y |
0,006 |
0,003 |
0,006 |
|
|
2 |
X |
0,006 |
0,009 |
0,003 |
|
Y |
0,008 |
0,001 |
0,003 |
|
|
3 |
X |
0,009 |
0,011 |
0,007 |
|
Y |
0,005 |
0,006 |
0,005 |
|
Источник: составлено автором на основе полученных данных в ходе исследования.
Также в работах «Исследование точности определения координат точек спутниковым приемником в режиме РТК», «Сравнительный анализ точности спутниковых определений в различных режимах измерений» авторы пришли к схожим СКП [14, 15].
Заключение
В таблицах выше приведены СКП базисов и координатных определений отдельно по каждому циклу наблюдений, для более репрезентативного отображения данных и исключения влияния случайных ошибок ниже рассмотрим СКП которые рассчитаны суммарно с учетом всех серий измерений.
Базовая станция находилась на удалении 4 км от ровера. Априорная СКП в таком случае будет равна 14 мм. Фактическая СКП в режиме RTK составила 11 мм, фактическая СКП с использованием технологии VRS составила 7 мм, то есть результат лучше на 36 %. Если из фактической СКП вычесть увеличение погрешности за увеличение расстояния до базовой станции (1 мм/км = 4 мм), получим такое же СКП, как и с использованием технологии VRS. Исходя из этого, можно сделать вывод о том, что фактическая СКП координат виртуальной базовой станции равняется нулю. Априорная СКП спутникового оборудования в режиме VRS будет подчинена той же формуле, что и при работе в режиме классической RTK.
Общая СКП базисов в режиме RTK по всем циклам наблюдений составила 13 мм, в режиме VRS – 7 мм.
Анализ определения длин базисов не показал существенного отличия от погрешности определения плановых координат, исходя из чего можно сделать вывод о том, что холодная и относительная погрешности являются одинаковыми как для режима измерений RTK, так и для режима измерений RTK с использованием технологии VRS.
Конфликт интересов
Благодарности
Библиографическая ссылка
Жимагулов Д.К. ИССЛЕДОВАНИЕ ТОЧНОСТИ КИНЕМАТИКИ В РЕАЛЬНОМ ВРЕМЕНИ С ИСПОЛЬЗОВАНИЕМ ВИРТУАЛЬНОЙ БАЗОВОЙ СТАНЦИИ // Успехи современного естествознания. 2025. № 10. С. 51-56;URL: https://natural-sciences.ru/ru/article/view?id=38442 (дата обращения: 26.02.2026).
DOI: https://doi.org/10.17513/use.38442



