Введение
В рамках стратегий развития стран и предприятий особое внимание уделяется текущему состоянию и вектору развития отечественного минерально-сырьевого комплекса [1; 2]. Актуальность проблемы снижения числа легкообогатимых руд и усложнения горно-геологических условий добычи и схем переработки в контексте повышения спроса на стратегические металлы и контроля за соблюдением экологических требований способствует вовлечению в переработку техногенных месторождений и отходов недропользования [3-5].
Высокоградиентная магнитная сепарация (ВГМС) является одним из основных методов извлечения тонкоизмельченных слабомагнитных материалов из минерального природного и техногенного сырья [6-8] и, на фоне растущих требований к эффективности и экологичности процессов разделения магнитных частиц, может применяться во многих отраслях – от горнодобывающей промышленности до биотехнологий и очистки технических жидкостей [9; 10].
Экспериментальное исследование магнитных и гидродинамических явлений, происходящих внутри рабочей зоны ВГМС, связано с большими временными и финансовыми затратами, а также техническими ограничениями. В этих условиях математическое моделирование становится мощным инструментом анализа и оптимизации процессов, позволяя детально исследовать распределение магнитного поля, движение частиц и гидродинамику пульпы без необходимости дорогостоящих экспериментов. Применение численных методов, таких как FEM, CFD и DEM, открывает возможность для создания мультифизических моделей, которые обеспечивают глубокое понимание взаимосвязей между параметрами конструкции и технологическими показателями процесса [11].
Несмотря на широкое распространение методов численного моделирования, в настоящее время отсутствует единый алгоритм или методологически обоснованный подход, учитывающий специфику магнитно-гидродинамических процессов, протекающих в матричных системах ВГМС. При этом именно комплексное описание взаимодействия магнитных, гидродинамических и механических факторов определяет достоверность и инженерную применимость результатов моделирования. Следует отметить, что в отечественной научной и проектной практике такие подходы развиты недостаточно: публикации, посвященные моделированию матриц ВГМС, носят фрагментарный характер и не формируют целостной методологии оптимизации конструктивных параметров.
Проведение комбинированных исследований, включающих методы компьютерного моделирования, демонстрирует существенные преимущества по сравнению с традиционными экспериментальными исследованиями благодаря ресурсной эффективности, обеспечивающей значительное снижение материальных и временных затрат при сохранении высокой точности результатов [12]. Среди достоинств моделирования также стоит отметить масштабируемость, позволяющую моделировать сложные многоуровневые системы, и управляемость процесса, дающую возможность варьирования временных параметров и многократного повторения экспериментов [13; 14].
Современный этап характеризуется использованием сложных многомасштабных моделей, интеграцией различных физических процессов (магнитных, гидродинамических, механических), а также применением универсальных программных платформ – таких как COMSOL Multiphysics [10], Ansys [15] и др. Моделирование становится неотъемлемой частью процесса проектирования и модернизации сепараторов, позволяя существенно сократить экспериментальные затраты и повысить эффективность технологий на этапе НИОКР.
Таким образом, цель данной работы заключается в обосновании методологического подхода к оптимизации конструктивных параметров матрицы высокоградиентного магнитного сепаратора методом моделирования для повышения эффективности сепарации минерального и техногенного сырья.
Материалы и методы исследования
Исследование выполнено в формате систематического обзора научной и технической литературы по тематике моделирования процессов высокоградиентной магнитной сепарации. Основным источником информации послужили рецензируемые публикации в международных журналах, индексируемых в базах данных ВАК, Scopus и Web of Science, а также статьи из профильных конференций по прикладной механике, физике магнитных явлений и обогащению полезных ископаемых. Проведен анализ 120 источников отечественных и зарубежных авторов, опубликованных в рецензируемых журналах и сборниках конференций, из которых 41 отобран для детального изучения.
Исследование основано на принципах системности и междисциплинарного анализа. В качестве основного инструмента использован структурированный обзор научных публикаций, отражающих применение математического и программного моделирования в технологических задачах, решаемых с применением высокоградиентной магнитной сепарации.
Результаты исследования и их обсуждение
Направления моделирования в области ВГМС
На основе анализа научно-технической литературы была проведена систематизация исследований в области ВГМС, направленных на разработку эффективных технологических решений и совершенствование конструкций с применением моделирования (табл. 1).
Основываясь на анализе полученных данных, представленных в таблице 1, авторы определили пять основных направлений исследований в области ВГМС, в которых для достижения различных целей использовались результаты моделирования: изучение поведения (движения) частиц, изучение характеристик магнитного поля, оптимизация геометрических параметров и материала матричных элементов, исследование влияния параметров материала на показатели магнитной сепарации и обоснование конструкции матричного блока.
Первое направление объединяет исследования, в которых моделирование используется как для оптимизации уже существующих конструкций, так и для разработки принципиально новых матриц и сепараторов. Основной подход заключается в моделировании и анализе распределения магнитного поля и магнитного градиента, включая расчет баланса сил и вероятности захвата частиц [10; 16; 17]. Важным аспектом является подбор конструкции стержневых матриц и их геометрических параметров для достижения заданной селективности разделения: диаметр стержней и шаг сетки определяют эффективность разделения крупной и мелкой фракций, что подтверждается экспериментально на полупромышленных и промышленных образцах [18]. Современные методы, включая двумерное и трехмерное МКЭ-моделирование [19], также позволяют прогнозировать локальные изменения поля, оценивать величину магнитного градиента и уточнять распределение потоков.
Второе направление включает в себя исследования влияния характеристик частиц на захват и эффективность выделения слабомагнитных минералов. Стоит отметить, что перспективным является применение ВГМС с циркулирующей магнитной жидкостью [20-22], то есть добавлением раствора MnCl2 в пульпу для повышения контрастности магнитных свойств разделяемых минералов. Результаты численного моделирования процесса захвата частиц согласуются с результатами экспериментов и также подтверждают преобразование конкурирующего процесса захвата в механический захват при обработке слабомагнитных минералов с помощью технологии высокоградиентной магнитной сепарации с использованием магнитной жидкости (HGMSCMF).
Задачами исследований третьего направления является определение оптимальной формы поперечного сечения матричного элемента и соотношения его сторон, а также изучение состояния намагниченности матриц и влияния намагниченности (насыщения) матрицы на эффективность захвата частиц.
В работе [23] авторы доказывают, что форма и материал матрицы значительно влияют на процесс достижения матричным элементом насыщения и наибольшего градиента напряженности магнитного поля. Интерпретируя результаты сравнения магнитной силы, можно сделать вывод о том, что эллиптическая и квадратная матрицы могут генерировать гораздо большую магнитную силу в широком диапазоне расстояний от поверхности.
При этом магнитная сила ромбовидных матриц велика вблизи поверхности, но быстро уменьшается с увеличением расстояния от поверхности. Таким образом, путем подбора оптимальной формы матричного элемента можно повысить извлечение полезных компонентов в концентрат.
В ряде исследований [11; 24; 25] с применением комплексных и численных методов моделирования установлено, что форма и соотношение сторон магнитных матриц существенно влияют на эффективность захвата частиц в высокоградиентных магнитных сепараторах. Показано, что эллиптические, ромбовидные и прямоугольные матрицы, ориентированные вдоль магнитного поля, обеспечивают больший радиус захвата и более высокую эффективность разделения по сравнению с круглыми элементами, особенно при умеренных значениях магнитной индукции. Выявлено существование оптимального соотношения сторон матрицы, которое уменьшается с ростом магнитной индукции и не зависит от размера частиц, что позволяет повысить извлечение ультрадисперсных магнитных минералов и снизить энергозатраты при разработке ВГМС-систем.
Таблица 1
Направления моделирования в области ВГМС
|
Направление исследований |
Разработанная модель |
Программа / Метод |
Исследуемые параметры |
Ист. |
|
Исследование новых конструкций матричного блока |
Модель траектории движения частиц в потоке жидкости и магнитном поле |
COMSOL Multiphysics / FEM, DEM |
Область действия магнитного поля, создаваемого матричным элементом |
10; 16 |
|
QuickField software |
Распределение магнитного поля мембранной матрицы |
9 |
||
|
Модель распределения магнитного поля в рабочем пространстве кассеты / Визуализация индукции поля (магнитная карта) |
FEM |
Магнитные карты поперечных сечений кассет (матриц) разного типа в сепараторах со сверхпроводящими магнитными системами |
17 |
|
|
2D- и 3D-модели распределения магнитного поля в рабочем пространстве матрицы из нержавеющей стали (с применением сверхпроводящего соленоида) |
FEM / OPERA-3D |
Распределение магнитного поля в матричной системе из стальных стержней из нержавеющей стали |
19 |
|
|
Модель оценки траектории частиц для стержневых матриц |
н/д |
Траектории движения частиц при варьировании диаметра и степени заполнения стержневой матрицы, глубины расположения матрицы в направлении потока пульпы |
18 |
|
|
Исследование влияния параметров сырья на технологические показатели ВГМС |
Модель ВГМС с циркулирующей магнитной жидкостью (HGMSCMF) |
COMSOL Multiphysics / FEM, DEM |
Захват частиц различного размера |
22 |
|
Захват частиц с различными магнитными свойствами |
20; 21 |
|||
|
Оптимизация геометрических параметров и материала матричных элементов |
Модель ВГМС с разной формой и конфигурацией матричных элементов |
ANSYS software, COMSOL Multiphysics; Ansys fluent; EDEM / CFD; FEM; DEM |
Распределение магнитного поля при разной форме поперечного сечения матричного элемента (круглая, эллиптическая, квадратная, ромбовидная и др.) при заданной конфигурации матрицы |
11; 23; 24; 25 |
|
Расширенные модели захвата частиц в ВГМС, учитывающие магнитные и гидродинамические силы |
Распределение магнитного поля и определение траекторий движения частиц при разном значении отношения длинной оси матричного элемента к короткой |
26; 27 |
||
|
Модель ВГМС с различным уровнем намагниченности (насыщения) матричных элементов |
Ansys, COMSOL Multiphysics / FEM |
Распределение магнитного поля в зависимости от намагниченности (насыщения) матричного элемента при различном соотношении сторон |
15; 28; 29 |
|
|
Изучение характеристик магнитного поля |
3D-модель ВГМС с эллиптической матрицей |
Ansys, Magneto / FEM |
Влияние горизонтального зазора и длины длинной оси матрицы на силовые показатели магнитного поля |
30 |
|
Модель ВГМС с различными формами осадительных элементов |
Влияние формы поперечного сечения (равностороннего треугольника, квадрата, шестиугольника, восьмиугольника, додекагона и круга) на характеристики распределения магнитного поля |
31 |
||
|
Изучение движения частиц в ВГМС |
Модели отклика (Response Surface Methodology, RSM). Нейросетевое моделирование (Artificial Neural Networks, ANN) |
Используется внутреннее ПО компаний – производителей оборудования |
Траектории частиц с учетом влияния их формы, скорости вращения матрицы и скорости подачи материала на траекторию движения частиц |
32 |
|
Модель распределения поля и потока вокруг матрицы |
COMSOL Multiphysics / МКЭ |
33; 34 |
||
|
Модель расчета траектории движения частиц |
35 |
|||
|
Модель накопления частиц на матричном элементе |
SBM-sw и SBM-dw / COMSOL Multiphysics, Matlab |
Профиль накопления частиц при определенных параметрах (влияние пульсирующей суспензии, расстояния между проволоками и приложенной магнитной индукции) |
36; 37; 38; 39 |
|
|
Модель захвата частиц |
Расстояние между магнитными проволоками, расстояние между слоями магнитных проволок, диаметр элемента |
40 |
Источник: составлено авторами на основе полученных данных в ходе исследования.
В работе [26] предложена концепция соответствия между геометрией матрицы и магнитной индукцией, при котором достигается максимальный радиус захвата частиц; оптимальное соотношение сторон зависит от величины индукции и не связан с размерами частиц или матрицы. В исследовании [27] уточнено соотношение размеров магнитного элемента и частицы, обеспечивающее максимальный захват, выведены уравнения для магнитной силы и сопротивлениям и определены условия захвата.
В работе [15] методом численного моделирования изучено влияние соотношения сторон и степени намагниченности матриц из железа и стали SUS430 на эффективность улавливания частиц; показано, что с ростом значения коэффициента соотношения сторон расширяется диапазон индукций, при которых достигается насыщение и повышается эффективность захвата слабомагнитных минералов. В исследовании [28] разработана математическая модель для прогнозирования состояния намагниченности и учтено влияние магнитных взаимодействий между элементами, зависящих от угла между полем и линией их соединения, что позволяет оптимизировать конфигурацию матрицы и снижать энергопотребление. В работе [29] установлена зависимость намагниченности от формы и ориентации матрицы в магнитном поле, доказано влияние геометрии поперечного сечения на точность расчетов и степень намагничивания.
Четвертое направление посвящено изучению характеристик магнитного поля, создаваемого в ВГМС, включая анализ особенностей распределения магнитного потока и установление взаимосвязей между геометрией матрицы и силовыми показателями магнитного поля.
В работе [30] численным моделированием и экспериментами показано, что в многоматричных системах с эллиптическими матрицами усиливается взаимодействие индуцированных полей, что повышает магнитную индукцию, но снижает градиент поля и магнитную силу, сокращая зону захвата частиц. Оптимизация расстояния между матрицами и их размеров позволяет регулировать уровень накопления частиц на осадительном элементе, при этом расхождение между расчетными и экспериментальными данными не превышает 4,3%. В исследовании [31] установлено, что форма поперечного сечения влияет на параметры магнитного поля: по интенсивности поля и градиента они убывают в ряду треугольник – квадрат – шестиугольник – восьмиугольник – додекагон – круг; применение зубчатых пластин вместо цилиндров повышает извлечение ильменита до 45% при тех же условиях намагничивания.
Пятое направление посвящено изучению поведения частиц в ВГМС. При помощи различных программных пакетов рассчитывается траектория движения и устанавливаются закономерности захвата и накопления матрицей мелких частиц минералов с целью увеличения селективности и эффективности сепарации.
В работе [32] рассмотрены модели движения частиц в магнитном поле сепаратора, включая механистические, статистические и нейросетевые (ANN) подходы; показано, что физически точные модели сложны в применении, тогда как ANN-модели эффективны для прогнозирования, но не раскрывают физику процесса. В исследованиях [33] и [34] с помощью моделирования и экспериментов установлено, что асимметричные пульсации и регулирование скорости потока повышают селективность разделения, а оптимизация формы импульсов предотвращает засорение матрицы. В работе [35] методом конечных элементов смоделировано влияние скорости подачи и вращения матрицы в центробежной ВГМС, показано образование спирального потока и сдвиговых напряжений, улучшающих селективность и эффективность разделения.
В работах [36; 37] представлена статическая модель SBM, описывающая накопление частиц на матрице с учетом влияния магнитной индукции, скорости потока и геометрии элементов, позволяющая прогнозировать профиль и массу осадка. Однако для реальных условий предпочтительнее динамические модели: в [38] предложена зависимая от частоты пульсаций модель, учитывающая влияние магнитных и гидродинамических сил на скорость образования отложений. В [39] показано, что поочередная подача мелкой и крупной фракции повышает извлечение и селективность – массовая доля захваченных частиц до 20 мкм увеличивается более чем вдвое, а содержание железа возрастает до 62%. В исследовании [40] с использованием имитационного моделирования предложена комбинированная вращающаяся матрица, обеспечивающая повышение эффективности центробежной ВГМС при разделении мелкодисперсных руд.
Таблица 2
Характеристика методов CFD, FEM и DEM в области ВГМС
|
Метод |
Процесс |
Область применения |
Цель моделирования |
Допущения, упрощения |
|
FEM |
Моделирование магнитного поля |
Генерации точного распределения магнитного поля в геометрически сложных конфигурациях (основано на решении уравнений Ньютона для каждой отдельной частицы) |
Оптимизация геометрии матриц ВГМС (форма, конфигурация и т.д.) |
Увеличение числа узлов FEM и ячеек FVM резко повышает вычислительные затраты. Для 3D-моделирования рекомендуется объединение расчетов FEM и CFD в одной сетке |
|
CFD |
Моделирование гидродинамики |
Магнитные диполь-дипольные взаимодействия (на основе уравнений Розенсвейга и Сато), механические силы (упругость, демпфирование), центробежные силы (при моделировании MEC – магнитно-усиленной центрифугирования) |
Движение жидкости (носителя частиц) – скорость, давление, вихри, траектории частиц в потоке. CFD показывает, куда и как «плывут» частицы, прежде чем начнут взаимодействовать между собой |
Не учитывает взаимодействие частиц между собой – ни магнитное, ни механическое. Результаты моделирования более достоверны, когда частицы разрежены и не сталкиваются |
|
DEM |
Моделирование взаимодействий частиц |
Моделирование потока жидкости, в который встроено FEM-поле. Движение частиц анализируется с учетом действующих магнитных и гидродинамических сил (используется сила Лоренца) |
Моделирование агломерации частиц с учетом контактных сил, исследование влияния центробежной силы, анализ формы и плотности осадка |
Магнитные частицы рассматриваются как магнитные диполи, даже несмотря на то, что их ядра не бесконечно малы. Поле вокруг более чем одного диполя не рассчитывается точно, так как их поля взаимодействуют, усиливая или ослабляя друг друга. В моделировании учитывается только ближайший элемент в системе частиц. Гидродинамические силы влияют на кинетику, но не изменяют окончательную форму осадка или его устойчивость к центробежным силам. Поверхностные силы, включая капиллярные, пренебрегаются, что допустимо при рассматриваемых размерах частиц. Магнитные частицы не искажают поле. Для упрощения модели считается, что все частицы выстраиваются вдоль направления внешнего магнитного поля |
Источник: составлено авторами на основе полученных данных в ходе исследования.
Комплексное моделирование протекающих при ВГМС процессов
Комплексное моделирование с использованием трех методов (CFD, FEM и DEM) показывает высокую степень реалистичности и является перспективным подходом для оптимизации процессов ВГМС. Суть комбинированного метода заключается в расчете магнитных полей с помощью метода конечных элементов (FEM), результаты которого загружаются в моделирование как в CFD (вычислительную гидродинамику), так и в DEM (метод дискретных элементов). Особенности вышеперечисленных методов представлены в таблице 2.
Как было отмечено ранее, важным направлением является вычисление траектории и вероятности улавливания и удержания частицы на матричном осадительном элементе.
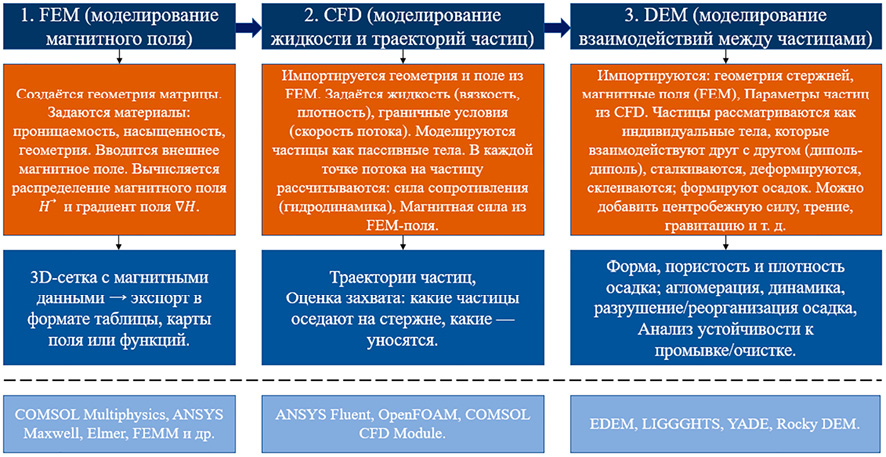
Рабочий алгоритм комплексного моделирования ВГМС-процессов Источник: составлено авторами на основе полученных данных в ходе исследования
Расчет и, как следствие, моделирование поведения частиц в рабочей зоне сепаратора сводится к решению уравнения баланса сил, действующих на частицу. Для крупных частиц наибольшее влияние оказывает сила тяжести, для мелких – вязкое сопротивление. В мокрой сепарации необходимо, чтобы магнитная сила превышала гидродинамическое сопротивление, в то время как в сухой сепарации – силу тяжести [41]. Данный баланс сил справедлив, если разделение на фракции происходит в воде. Если в рабочую зону сепаратора добавляются парамагнитные вещества (например, MnCl2), повышающие контрастность магнитных свойств разлепляемых частиц, то необходимо также учитывать данный эффект при расчете и моделировании протекающих процессов [21].
ВГМС – сложный физико-технический процесс, где участвуют магнитные поля, жидкости (поток), частицы и их взаимодействия. На основе проведенных исследований предложен алгоритм моделирования, представленный на рисунке.
Представленный на рисунке алгоритм иллюстрирует интегрированный подход к численному моделированию процессов высокоградиентной магнитной сепарации, включающий три взаимосвязанных этапа. На первом этапе (FEM) проводится моделирование магнитного поля: создается геометрия матрицы, задаются физические свойства материалов и рассчитываются распределения магнитного потенциала и градиента поля. На втором этапе (CFD) моделируется движение жидкости и траектории частиц с учетом магнитных и гидродинамических сил, что позволяет определить зоны осаждения и оценить эффективность захвата. На третьем этапе (DEM) анализируются взаимодействия между частицами, формирование и разрушение агломератов, устойчивость и структура осадка. Такой комплексный подход обеспечивает детальное понимание взаимосвязей между магнитными, гидродинамическими и механическими процессами в зоне разделения и используется для оптимизации конструкции и режима работы ВГМС-систем.
Заключение
В условиях роста требований к эффективности и селективности процессов обогащения применение математического моделирования в задачах высокоградиентной магнитной сепарации становится неотъемлемой частью научно-технического прогресса.
В результате проведенного обзора и анализа научных публикаций по тематике математического моделирования процессов высокоградиентной магнитной сепарации установлено, что моделирование является эффективным инструментом для оптимизации конструкции сепараторов и повышения эффективности процессов разделения. Показано, что применение численных методов позволяет комплексно учитывать магнитные, гидродинамические и механические взаимодействия, обеспечивая высокую точность воспроизведения реальных условий работы оборудования.
Обосновано, что использование методов математического моделирования при проектировании и модернизации ВГМС-систем позволяет существенно сократить объем экспериментальных работ, повысить точность прогнозирования технологических параметров и снизить затраты на НИОКР. Показан методологический подход к оптимизации конструкции матрицы ВГМС на основе мультифизического моделирования, включающего совокупное применение методов конечных, дискретных элементов и вычислительной гидродинамики.
Таким образом, подтверждена целесообразность интеграции математического моделирования в процесс конструирования и совершенствования высокоградиентных магнитных сепараторов как ключевого инструмента повышения эффективности технологий переработки минерального и техногенного сырья.
Конфликт интересов
Финансирование
Библиографическая ссылка
Степанов Д.В., Александрова Т.Н., Николаева Н.В. МОДЕЛИРОВАНИЕ ПРОЦЕССОВ ВЫСОКОГРАДИЕНТНОЙ МАГНИТНОЙ СЕПАРАЦИИ: ОБЗОР МЕТОДА И АЛГОРИТМ КОМПЛЕКСНОГО ПОДХОДА // Успехи современного естествознания. 2025. № 12. С. 47-55;URL: https://natural-sciences.ru/ru/article/view?id=38465 (дата обращения: 10.03.2026).
DOI: https://doi.org/10.17513/use.38465



