Как показывают проведенное численное моделирование, существует минимальное количество 
членов разложений, обеспечивающее выполнение всех ограничений экстремальной задачи. Для варианта начальных условий и основных параметров моделирования [2], сочетания собственного и заемного оборотного капитала моделируемой ФХД МЭЗ на начало интервала управления - B0 = 20 000 000 руб., K0 = 80 000 000 руб. - минимальное количество членов разложений неизвестных функций управления [2;(6)] 
.
|
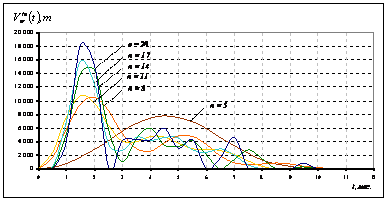
Рисунок 1. Аппроксимация оптимальной функции поставок
|
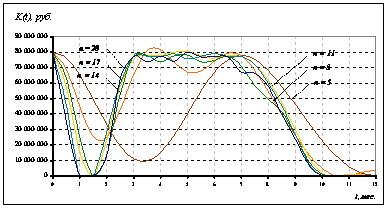
На рис.1 и 2 представлена динамика сходимости приближений неизвестных функций поставок маслосемян подсолнечника На рис.3 приведен график зависимости значений оптимизированного критерия качества ФХД МЭЗ [2;(1)] от количества удерживаемых членов разложений функций управления [2;(6)]. Дополнительные исследования сходимости рядов Фурье, аппроксимирующих неизвестные функции управления, показывают монотонную сходимость решения к оптимальному с увеличением количества удерживаемых членов разложения n. Для заданных начальных условий моделирования уже при n = 17 получаемые приближения критерия качества [2;(1)] отличаются друг от друга менее чем на 1,5%. Данное обстоятельство подтверждает правомочность удержания первых 20-ти суммовых членов разложения неизвестных функций оптимизационной математической модели ФХД МЭЗ с заданными начальными условиями и основными параметрами моделирования [2]. |
|
Рисунок 2. Аппроксимация оптимальной функции кредитования |
рядом Фурье для различного количества удерживаемых в разложении членов n
к оптимальному решению в зависимости от количества удерживаемых в разложениях [2;(6)] членов рядов Фурье (n = 5, 8, 11, 14, 17, 20).
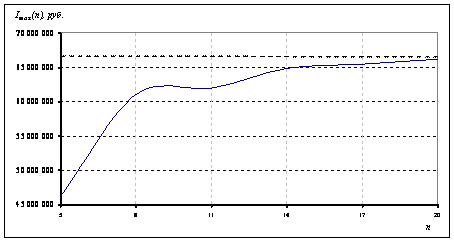
Рисунок3. Динамика сходимости максимизированного критерия качества от количества удерживаемых в разложении членов n
Необходимо заметить, что приближения решения оптимизационной математической модели [1;(1),(2)-(5)] в форме [1;(6)] абсолютно и равномерно сходятся к истинному для любого сочетания начальных условий и основных параметров моделирования в силу свойства абсолютной и равномерной сходимости рядов Фурье, эти решения аппроксимирующих. Однако в каждом конкретном случае требуется дополнительное исследования на и количество членов разложений [2;(6)], обеспечивающих приемлемую точность получаемого решения для функций управления.
СПИСОК ЛИТЕРАТУРЫ
- Гуров Д.О. Оптимизационная математическая модель финансово-хозяйственной деятельности предприятия. Современные сложные системы управления (HTCS´2004): Материалы IV международной конференции. - Тверь: ТГТУ, 2004. - с.243-247.
- Гуров Д.О. Задача оптимизации финансово-хозяйственной деятельности предприятия в рядах Фурье. Современные сложные системы управления (HTCS´2004): Материалы IV международной конференции. - Тверь: ТГТУ, 2004. - с.248-252.
- Ванько В.И., Ермошина О.В., Кувыркин Г.Н. Вариационное исчисление и оптимальное управление. - М.: Изд-во МГТУ им. Н.Э. Баумана, 2001.
Библиографическая ссылка
Гуров Д.О. ИССЛЕДОВАНИЕ СХОДИМОСТИ РЕШЕНИЙ ЗАДАЧИ ОПТИМИЗАЦИИ ФИНАНСОВО-ХОЗЯЙСТВЕННОЙ ДЕЯТЕЛЬНОСТИ МАСЛОЭКСТРАКЦИОННОГО ПРОИЗВОДСТВА // Успехи современного естествознания. – 2005. – № 2. – С. 60-61;URL: https://natural-sciences.ru/ru/article/view?id=8009 (дата обращения: 19.04.2024).