Научный журнал

Успехи современного естествознания

ISSN 1681-7494

"Перечень" ВАК

ИФ РИНЦ = 0,775

• Авторы
• Файлы

Жариков Д.Н. Лукьянов В.С.

Статья в формате PDF

145 KB

Введение

В настоящее время ведутся работы по объединению вычислительных центров в сети. Подобная структура, именуемая Грид (GRID), позволяет организовать вычисления, передачу, обработку и хранение данных в режиме разделения. Систему GRID лучше всего представлять себе как граф: его вершины - вычислительные центры (обычно кластеры), а дуги - линии связи между ними (оптоволокно). Кластера способны обмениваться возникающими на них заданиями, для увеличения производительности системы.

Здесь сразу же встает вопрос: «Как оптимально выбрать узел для выполнения задания?». Подобные исследования уже проводились. В ИСП РАН в рамках работ по параллельным вычислениям разрабатывали среду для имитационного моделирования работы грид. Учитывая перспективность данного направления, мы решили провести самостоятельные исследования в данной области. Также перед нами была поставлена задача оценки надежности моделируемой грид-системы. Каждый кластер в нашей модели представляет собой совокупность независимых узлов, каждый из которых может выходить из строя в случайный момент времени и может восстанавливаться через некоторый случайный интервал времени. Наша модель, в отличие от модели ИСП РАН, получилась стохастической, а не детерминированной. Затем, после проведения нескольких тестов, была добавлена возможность случайной генерации потока задач. Основной задачей нашей модели является оценка качества распределения заданий на различных предложенных нами стратегиях с учетом влияния надежности узлов.

Описание стратегий распределения задач

Во всех нижеописанных стратегиях узлам присваиваются стоимости выполнения задания. Фактически это целевая функция, которую надо минимизировать. Чем меньше стоимость, тем выгоднее выполнять задание на узле. Оценка производится только для тех кластеров, которые доступны по сети. Доступным по сети является узел, который может быть достигнут по графу из узла, на котором появилось задание. Недоступные узлы всегда получают оценку ∞. Если два кластера получают одинаковую оценку, то выбирается случайный из них.

Понятно, что оценка должна отвечать хотя бы двум критериям:

• Адекватно оценивать загруженность кластера.
• Быть легко вычисляемой, т.е. высчитываемой по относительно простой формуле.

Случайный кластер. Каждый кластер получает себе в качестве оценки случайное число, равномерно распределенное по интервалу [0;1). Эта система удобна, когда все задания генерируются на одном кластере или небольшой группе кластеров, а все кластеры одинаковые по производительности.

Наибыстрейшего выполнения.

,

где  - предполагаемое время выполнения задания на кластере,  - предполагаемое время пересылки задания по сети до узла, - предполагаемое время обратной пересылки результата вычислений,  - время, оставшееся до окончания исполнения i-го задания на кластере в текущий момент времени задания,  - предполагаемое время исполнения j-го задания из очереди,  и  - количество узлов, на которых будут исполняться задания, W - количество узлов кластера.

Создатель. Кластер создатель получает оценку в 1.0, а все остальные кластера оценку в 100.0. Данная стратегия реализует выполнение заданий на том же кластере, на котором они появились.

Стратегия минимального риска. Среднее время работы на кластере одного узла, деленное на количество требуемых заданию узлов, представляет собой (при допущении пуассоновского потока отказов и восстановлений) среднее время работоспособного состояния этой группы узлов. Поэтому в качестве оценки было взято , где  - предполагаемое время выполнения задания на кластере,  - среднее время безотказной работы одного узла, w - количество узлов, на которых будет исполняться задание.

Соотношения количества свободных узлов кластера и количества узлов, требуемых задачей. Оценка есть , где w - количество узлов, на которых будет исполняться задание, N - количество свободных узлов кластера. Используется при быстром выполнении заданий и в отсутствие очереди.

Минимальной сложности на узел кластера. Оценка = 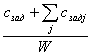, где  - сложность задания, для которого выбирается исполнитель,  - сложность j - го задания в очереди кластера, W - количество узлов кластера.

Оптимальной сложности. Оценка = 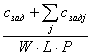, где  - сложность задания, для которого выбирается исполнитель,  - сложность j - го задания в очереди кластера, W - количество узлов кластера, L - количество ядер на узле, P - производительность узла.

Оптимального использования узлов. Оценка = 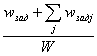, где  - количество узлов, необходимое заданию, для которого определяется кластер,  - количество узлов, необходимое j-му заданию в очереди кластера, W - количество узлов кластера.

Можно оценить один и тот же кластеру сразу по нескольку критериев, но для этого надо придумать способ объединения в одну. Был выбран следующий способ: , где W_i-оценка по i-му критерию, - вес i-го критерия, n-количество критериев, W - объединенная оценка.

Именно по этой объединенной оценке и будет выбираться кластер для исполнения задания.

Используемая имитационная модель надежности.

Оценку надежности каждого кластера будем проводить по следующим трем параметрам. Нам необходимо определить коэффициент готовности, среднее время безотказной работы, средняя время отказного состояния.

Одним из важнейших параметров системы из нескольких узлов является, на ряду с параметрами безотказной работы и восстановлений после отказа отдельного узла, размер резерва, а, точнее, соотношение размера резерва и количество используемых узлов в системе. Будем действовать предположении абсолютной надежности системы контроля и системы подключения резерва. Также имеется еще один важный параметр, который появляется в системе из нескольких узлов, - максимально число узлов, которое может восстанавливать параллельно, т. е. количество ремонтных линий.

Зависимость коэффициента готовности от размера резерва, имитационным способом, показывает, что сначала с ростом резерва коэффициент резко возрастает, а потом резко замедляет свой рост, поэтому существует оптимальное значение коэффициента готовности, выше которого наращивание резерва представляется не целесообразно. Оптимум может быть найдем аналитически или имитационно. В нашем случае используется имитационный вариант поиска, а аналитический предназначен только для подтверждения результатов.

Среднее время безотказной работы растет с ростом резерва. Причем этот рост не ограничен. Среднее время отказного состояния начинает сокращаться с ростом размера резерва. Однако наращивание его имеет смыл до определенного предела. Созданная нами модель позволяет найти это оптимальное количество.

Аналогично решает вопрос с количеством ремонтных линий. Путем моделирования находится оптимум, оптимальное число ремонтных линий. Линии не должны простаивать, но и их мало количество не должно сильно увеличивать время пребывание системы в отказном состоянии.

Также решается вопрос о приближение потоков событий к пуассоновским. Как показало моделирование, в большинстве случаев приближение пуассоновского потока дает довольно точный результат.

Аналитическое моделирования отказов и восстановлений узлов.

Для проверки имитационной модели мы предлагаем следующую аналитическую модель с допущением, что отказы и восстановления происходят под действием стационарного пуассоновского потока событий. Интенсивности потоков:λ - поток отказа узла, μ- поток восстановления одного узла.

Тогда рk - вероятность того, что в отказном состоянии находятся k узлов. Предельные (финальные) вероятности существуют и даются формулами Эрланга:

; , ;

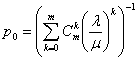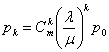Рассмотрим систему из m гомогенных узлов в предположении, что каждый из узлов отказывает и восстанавливается вне зависимости от других.

В случае, если в конкретный момент времени может восстанавливаться только один узел финальные вероятности будут иметь вид:

; ;

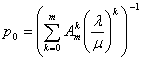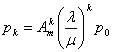После введения количества линий ремонта и резервирования вероятности будут даваться несколько более сложными формулами.

Пусть задание выполняется на m узлах. Отказ одного узла приводит к срыву задания. Поток переходов из рабочего состояния в отказное у системы в m раз больше, чем у одного узла. Поэтому среднее время пребывания в рабочем состоянии (при допущении пуассоновских потоков) стало в m раз меньше, т.е. среднее время безотказной работы одного узла.

Тестирование модели

Теперь, мы считаем, следует изложить особенности стратегий, которые были выявлены путем моделирования.

Самый лучший результат на таких категориях заданий дают стратегии: Наискорейшего исполнения; Соотношения свободных узлов кластера; Минимальной сложности на узел; Оптимальной загрузки. Стратегия Наискорейшего исполнения требует значительного числа вычислений для получения оценки, поэтому ее использование не рационально.

Стратегия Минимального риска сильно снижает число заданий выполнение, которых было прервано выходом узла из строя. Однако остальные показатели у нее несколько хуже. Также необходимо отметить, что при более детальном рассмотрении этой стратегии выяснилось, что она передает все задания на самые надежные и/или самые высокопроизводительные узлы грида.

Самый плохой результат дают стратегии Случайного хоста и Оптимального использования узлов. Это можно было предугадать заранее. Стратегия Случайного хоста работает плохо, т.к. структура крайне ассиметрична и задания появляются по всюду, а не в одном месте, как предполагалось при ее определении. Стратегия Оптимального использования узлов не учитывает сложности задач в очереди, а учитывает только количество требуемых им узлов.

Заключение

В результате проделанной работы нами было получено средство оценки стратегий распределения заданий по узлам грида. В перспективе можно попробовать решить обратную задачу. То есть на заданном множестве оценок определить такие веса стратегий, при которых параметры использования системы будут оптимальными. Однако эта задача требует значительного числа вычислительных ресурсов.

СПИСОК ЛИТЕРАТУРЫ

1. Каменщиков, М. А. Сервисы GRID, как объекты стандартизации [Электронный ресурс] / М. А. Каменщиков. - Режим доступа: http://jre.cplire.ru/jre/dec03/4/text.html.
2. Корягин, Д. Эволюция и проблемы Grid [Электронный ресурс] / Д. Корягин, В. Коваленко. - Режим доступа: http://www.osp.ru/os/2003/01/182396/_p2.html
3. Проблемы моделирования GRID-систем и их реализация [Электронный ресурс] / О.И. Самоваров [и др.]. - Режим доступа: http://agora.guru.ru/abrau2008/pdf/050.pdf

Библиографическая ссылка