В этой связи, нами была осуществлена оптимизация суммарных затрат (Y) (убытки, связанные с неопределенностью в процессе принятия управляющих решений (Y1) и стоимость прогнозирования (Y2), причем, Y=Y1 +Y2). Зависимость Y(X) характеризуется снижением суммарных затрат до определенного предела, после которого она начинает расти, т.к. с этого момента затраты на убытки, связанные с неопределенностью при принятии решений превышают затраты на прогнозирование. Как показывает опыт, затраты Y1(X) с увеличением X снижаются, а затраты Y2(X) с увеличением X растут. Соответственно, можно установить такое значение X зависимости Y(X), которому будут соответствовать минимальные затраты Y. Для решения этой задачи воспользуемся методом кубической сплайн-интерполяцией [1, 2, 3]. Исходные данные для решения задачи оптимизации, для рассматриваемого нами предприятия, в нашем случае сведены в таблицу (табл.1).
Таблица 1. Зависимость точности прогнозирования от затрат на прогнозирование
|
Исходные данные |
|||
K |
65 |
71 |
73,5 |
|
X |
2 |
6 |
10 |
|
Y1 |
3,2 |
0,58 |
0,32 |
|
Y2 |
0,4 |
1,02 |
1,7 |
|
Суммарные затраты на прогнозирование Y1 и Y2 |
|||
Y |
1,46 |
1,42 |
1,92 |
Пусть интерполируемая функция Y(X) задана своими значениями Yi в узлах Xi, (i=0, 1, ..., n). Длину частичного отрезка [Xi-1, Xi] обозначим hi:
.
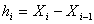Будем искать кубический сплайн на каждом из частичных отрезков [Xi-1, Xi]:
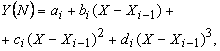
где 
- неизвестные постоянные (коэффициенты уравнения).
После нахождения необходимых коэффициентов задачи, подставляем полученные значения Y(X) в исходное выражение для кубического сплайна, определяем точку с оптимальными затратами [4]. Полученную оптимальную точку нанесем на график суммарной функции (рис. 1). Также построим зависимость 
на той же оси X, где отложена зависимость 
. После проведения расчетов необходимо установить в какой мере найденное значение Y отвечает минимуму затрат. Этому оптимальному 
также соответствует точка на кривой . При любом изменении количества прогнозов у нас получится ситуация при которой затраты будут возрастать.
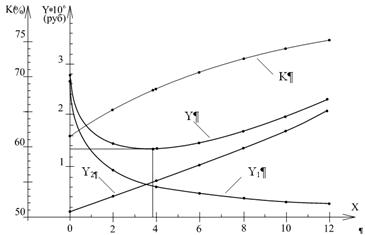
Рисунок 1. Зависимость Y1,Y2, Y, K от X и установление оптимальных Y*
СПИСОК ЛИТЕРАТУТРЫ
- Бахвалов Н.С. Численные методы. М.:Наука, 1973.
- Пирумов У.Г. Численные методы:Учеб. Пособие для студ. втузов. - 2-е изд., перераб. и доп. - М.:Дрофа, 2003. - 224с.:ил.
- Ильин В.А., Куркина А.В. Высшая математика: Учебник. - 2-е изд., перераб. и доп. - М.:ТК Велби, Изд-во Проспект, 2004. - 600 с.
- Пантелеев А. В., Летова Т.А. Методы оптимизации в примерах и задачах: Учеб. пособие -М.:Высш. шк., 2002. - 544с.: ил.
Библиографическая ссылка
Белоусов Н.В. УСТАНОВЛЕНИЕ ОПТИМАЛЬНОГО ПЕРИОДА ПРОГНОЗИРОВАНИЯ // Успехи современного естествознания. – 2005. – № 8. – С. 96-97;URL: https://natural-sciences.ru/ru/article/view?id=9137 (дата обращения: 23.11.2024).