Использование частично-рассогласованных предпочтений эксперта в методах вербального анализа решений позволит значительно расширить область их применения.
Для достижения этой цели необходимо решить следующие задачи:
- Определить текущий уровень рассогласованности.
- Согласовать рассогласованные предпочтения эксперта.
Данные задачи могут быть решены при помощи методов, относящихся к статистике объектов нечисловой природы.
Поскольку ответы эксперта являются объектами нечисловой природы, оценку согласованности очередного ответа эксперта с ранее полученными ответами предлагается проводить при помощи расстояния Кемени [2]. Для этого ответы эксперта о парном сравнении представляются в виде квадратной матрицы ![]() из 0 и 1 порядка
из 0 и 1 порядка ![]() , где k - количество элементов, которые необходимо сравнить между собой. При этом
, где k - количество элементов, которые необходимо сравнить между собой. При этом ![]() тогда и только тогда, когда
тогда и только тогда, когда ![]() или
или ![]() . В первом случае
. В первом случае ![]() , а во втором
, а во втором ![]() . При этом хотя бы одно из чисел
. При этом хотя бы одно из чисел ![]() и
и ![]() равно 1. Расстоянием Кемени между бинарными отношениями A и B, описываемыми матрицами
равно 1. Расстоянием Кемени между бинарными отношениями A и B, описываемыми матрицами 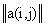 и
и![]() соответственно, называется число
соответственно, называется число ![]() , т.е. расстояние Кемени между бинарными отношениями равно сумме модулей разностей элементов, стоящих на одних и тех же местах в соответствующих им матрицах. Легко видеть, что расстояние Кемени - это число несовпадающих элементов в матрицах
, т.е. расстояние Кемени между бинарными отношениями равно сумме модулей разностей элементов, стоящих на одних и тех же местах в соответствующих им матрицах. Легко видеть, что расстояние Кемени - это число несовпадающих элементов в матрицах 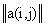 и
и![]() .
.
В качестве критерия согласованности ответов предлагается использовать следующую величину, называемою D-метрикой:
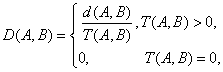 (1)
(1)
где:![]() - расстояние Кемени для отношений A и B,
- расстояние Кемени для отношений A и B,![]() . Величина D может принимать значения от 0 до 1, при этом значение «0» соответствует полной согласованности ответов эксперта, а «1» - полной рассогласованности.
. Величина D может принимать значения от 0 до 1, при этом значение «0» соответствует полной согласованности ответов эксперта, а «1» - полной рассогласованности.
Рассогласующиеся ответы эксперта хранятся по отдельности и считаются мнениями различных экспертов - «квазиэкспертов». При очередном ответе эксперта, он сравнивается с каждым элементом множества и присоединяется к тому элементу множества, с которым имеется полная согласованность. В том случае, если нет элементов, полностью согласующихся с этим ответом, формируется новый элемент множества ответов, в который переносятся ответы, ему не противоречащие.
Имеет смысл визуализировать данную форму хранения предпочтений экспертов для отображения пространственного рассогласования, показывая динамику ее накопления в ответах. На данной схеме будут наглядно отображены коалиции квазиэкспертов или отдельные «отшельники».
Для определения интегральной рассогласованности предлагается использовать величину Δ:
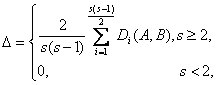 (2)
(2)
где s - количество «квазиэкспертов»,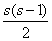 - количество расстояний Кемени.
- количество расстояний Кемени.
Существует несколько подходов к согласованию данных, имеющих нечисловую природу, а именно - ранжировок. Использование медианы Кемени имеет смысл, когда у экспертов есть основа для согласия, их ответы неравномерно распределены на множестве ранжировок [2]. Пусть 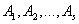 - матрицы отношений, описывающие мнения s экспертов. Для нахождения группового мнения необходимо вычислить медиану Кемени, (эмпирическое среднее относительно расстояния Кемени). Медианой Кемени является
- матрицы отношений, описывающие мнения s экспертов. Для нахождения группового мнения необходимо вычислить медиану Кемени, (эмпирическое среднее относительно расстояния Кемени). Медианой Кемени является ![]() , где
, где ![]() - расстояние Кемени. Элементы
- расстояние Кемени. Элементы ![]() удовлетворяют условию:
удовлетворяют условию: ![]() , если
, если ![]() , и
, и ![]() , если
, если ![]() . Следовательно, при нечетном количестве экспертов s, групповое мнение
. Следовательно, при нечетном количестве экспертов s, групповое мнение ![]() определяется однозначно. При четном s неоднозначность возникает в случае
определяется однозначно. При четном s неоднозначность возникает в случае ![]() . Тогда медиана Кемени
. Тогда медиана Кемени ![]() - не одна матрица отношений, а множество, при этом минимум суммы расстояний достигается и при
- не одна матрица отношений, а множество, при этом минимум суммы расстояний достигается и при ![]() , и при
, и при ![]() . Медиана Кемени определяет ранжировку, которая находится на наименьшем расстоянии от коллективного мнения группы экспертов.
. Медиана Кемени определяет ранжировку, которая находится на наименьшем расстоянии от коллективного мнения группы экспертов.
Для получения коллективного мнения экспертов используют методы средних баллов - метод средних арифметических рангов и метод медиан рангов. Для использования этих методов необходимо построить ранжировки ответов (от лучших к худшим). После построения происходит присвоение элементам ранжировки рангов таким образом, что первый элемент получает ранг 1, второй - 2 и т.д. В случае равноценности элементов, им присваивается средний ранг. Сумма рангов должна быть равна сумме порядковых номеров элементов в ранжировке.
При использовании метода средних арифметических рангов необходимо вначале подсчитать сумму рангов, присвоенных каждому элементу. Затем эта сумма делится на количество экспертов, в результате чего рассчитывается средний ранг каждого элемента, по которым строится итоговая ранжировка согласно принципу - чем меньше ранг, тем предпочтительней элемент. Метод некорректен, поскольку баллы измерены в порядковой шкале.
При использовании метода медиан рангов необходимо взять все ранги, соответствующие каждому элементу, и расположить их в порядке неубывания. Затем вычислить для каждого элемента медиану - среднее арифметическое центральных членов вариационного ряда и построить ранжировку согласно принципа - чем меньше ранг, тем предпочтительней элемент.
Метод согласования кластеризованных ранжировок позволяет перевести противоречия в специальным образом построенные кластеры, в то время как упорядочение кластеров соответствует одновременно всем исходным упорядочениям. Алгоритм согласования некоторого числа (двух или более) кластеризованных ранжировок состоит из трех этапов. На первом - выделяются противоречивые пары объектов во всех парах кластеризованных ранжировок. На втором - формируются кластеры итоговой кластеризованной ранжировки. На третьем этапе эти кластеры упорядочиваются. Для установления порядка между кластерами произвольно выбирается один объект из первого кластера и второй - из второго, порядок между кластерами устанавливается такой же, какой имеет место между выбранными объектами в любой из рассматриваемых кластеризованных ранжировок. Если в одной из исходных кластеризованных ранжировок имеет место равенство, а в другой - неравенство, то при построении итоговой кластеризованной ранжировки используется неравенство. Если два объекта из разных кластеров согласующей кластеризованной ранжировки окажутся эквивалентными в одной из исходных кластеризованных ранжировок (т.е. находиться в одном кластере), то необходимо рассмотреть упорядоченность этих объектов в какой-либо другой из исходных кластеризованных ранжировок. Если же во всех исходных кластеризованных ранжировках два рассматриваемых объекта находились в одном кластере, то естественно считать (и это является уточнением к этапу 3 алгоритма), что они находятся в одном кластере и в согласующей кластеризованной ранжировке. В дальнейшем, содержимое каждого кластера имеет смысл проанализировать с привлечением метода упорядочения по медианам рангов, либо вычислив медиану Кемени.
Нами предложен подход к согласованию ответов эксперта в целом (рассогласование выявлено при помощи показателя Δ) с участием самого эксперта. Согласование ответов эксперта в целом состоит из следующих этапов:
- расчет медианы Кемени;
- определение отношений, до которых расстояние Кемени от медианы Кемени максимально;
- определение ответов, приводящих к рассогласованию, и предъявление их эксперту, при этом ответы, полученные по транзитивному замыканию, не рассматриваются.
- определение уровня рассогласованности совокупности ответов эксперта. Если рассогласованность выше допустимого уровня, необходимо повторить процедуру экспертного согласования, иначе - продолжить опрос эксперта в стандартном режиме.
При согласовании пары отношений (рассогласование выявлено при помощи показателя 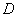 ) необходимо выполнить следующие шаги:
) необходимо выполнить следующие шаги:
- определение ответов, приведших к рассогласованию, и предъявление их эксперту, при этом ответы, полученные по транзитивному замыканию, не рассматриваются.
- определение уровня рассогласованности согласуемых отношений. Если рассогласованность выше допустимого уровня, следует повторить процедуру экспертного согласования, иначе - продолжить опрос эксперта в стандартном режиме.
Применение методов статистики объектов нечисловой природы в методах ВАР позволяет снять существенное ограничение, которым является требование непротиворечивости предпочтений эксперта, использовать методы ВАР при коллективном принятии решений.
СПИСОК ЛИТЕРАТУРЫ
- Ларичев О.И., Мошкович Е.М. Качественные методы принятия решений. - М.: Наука, 1996. - 206 с.
- Орлов А.И. Нечисловая статистика. - М.: МЗ-Пресс, 2004. - 513 с.
Библиографическая ссылка
Олейников Д.П., Бутенко Л.Н. ПРИМЕНЕНИЕ МЕТОДОВ СТАТИСТИКИ ОБЪЕКТОВ НЕЧИСЛОВОЙ ПРИРОДЫ В ВЕРБАЛЬНОМ АНАЛИЗЕ РЕШЕНИЙ // Успехи современного естествознания. 2005. № 9. С. 79-81;URL: https://natural-sciences.ru/ru/article/view?id=9209 (дата обращения: 06.03.2026).



