Ярус (LongLine) представляет собой крючковое орудие рыболовства (крючковую снасть, hooks and lines), состоящее из длинной веревки, называемой хребтиной (mainline), к которой на определенных расстояниях друг от друга крепятся рыболовные крючки. Троллы отличаются от ярусов тем, что они буксируются судном со скоростью 6-20 узлов.
В крючковых орудиях рыболовства широко используются канаты и веревки, которые служат для крепления крючков, буев, грузов и якорей к хребтине, а также для связи якоря с якорным буем.
Не смотря на то, что крючковыми орудиями рыболовства (КОР) ловят рыбу с глубокой древности (самый старый крючок относится к 7000 годам до рождества Христова), теории расчета и моделирования этих систем до последнего времени не было.
Расчет КОР сводится к определению формы, натяжения и сопротивления составляющих его веревок и канатов в потоке воды.
Впервые задачу о форме и натяжении гибкой тяжелой нити в поле сил тяжести решили три выдающихся математика Г. Лейбниц, И. Бернулли, Х. Гюйгенс в 1691 г. Они получили три первых интеграла уравнений равновесия гибкой нити:
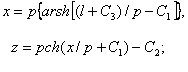
![]() . (1)
. (1)
Нами в [1] получены общие выражения для констант:
![]() .(2)
.(2)
Входящие в эти выражения величины ![]() определяются по формулам [1]:
определяются по формулам [1]:
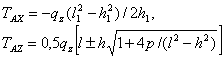 . (3)
. (3)
Уравнения (1-3) представляют собой математическую модель гибкой нити в поле сил тяжести и поле архимедовых выталкивающих сил. Они позволяют рассчитывать формы и натяжения любых канатов и веревок в воде при отсутствии течений.
При наличии течений математическая модель гибкой нити имеет вид:
 (4)
(4)
.![]()
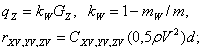
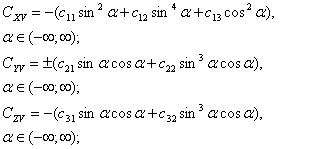
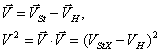
Математические модели якоря и рыболовного крючка:
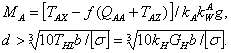 (5)
(5)
Для моделирования ярусов уравнения (1-5) необходимо дополнить граничными условиями в узловых точках, т.е. точках соединения якорных и буйковых линей, и крючковых поводцов с хребтиной.
Уравнения (1-5) позволяют рассчитывать формы, натяжения и сопротивления любых крючковых рыболовных систем как при наличии, так и при отсутствии течений.
СПИСОК ЛИТЕРАТУРЫ
- Габрюк В.И., Кулагин В.Д. Механика орудий рыболовства и АРМ промысловика. М.: Колос, 2000.-416 с.
- Габрюк В.И., Габрюк А.В., Осипов Е.В. Моделирование крючковых рыболовных систем. Владивосток: изд. ТИНРО-центра, 2004.- 120 с.
- Самарский А.А., Михайлов А.П. Математическое моделирование. - М.: ФИЗМАТЛИТ, 2002.- 320 с.
Библиографическая ссылка
Габрюк В.И. МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ КРЮЧКОВЫХ РЫБОЛОВНЫХ СИСТЕМ // Успехи современного естествознания. 2005. № 11. С. 27-28;URL: https://natural-sciences.ru/ru/article/view?id=9413 (дата обращения: 17.02.2026).



