Инерционная автоматическая передача является голономной системой и имеет три степени свободы. За обобщенные координаты приняты углы поворота ведущего звена, реактора и ведомого звена.
Математическая модель инерционной автоматической передачи [1], как голономной системы, получена на основе уравнения Лагранжа второго рода:
(1)
где 
- кинетическая энергия системы; 
,
,
- соответственно, обобщенные координаты, угловые скорости и силы.
После дифференцирования выражений кинетической энергии по обобщенным координатам, скоростям, необходимых преобразований и подстановки в уравнение (1) получим математическую модель автоматической передачи [1], использующей один импульс инерционного момента:
Участок разгона реактора:
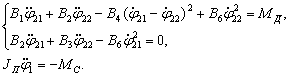(2)
Условием перехода является достижение угловой скорости реактора угловой скорости ведомого звена, т.е. 
Участок совместного движения реактора и ведомого звена:
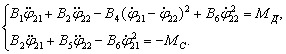(3)
Условием перехода является смещение центра тяжести неуравновешенной массы сателлита в относительном движении в область отрицательных значений инерционного момента, т.е. 
Участок торможения реактора:
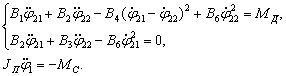(4)
Условием перехода является остановка реактора, т.е. 
Выстой реактора:
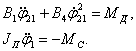(5)
Условием перехода является смещение центра тяжести неуравновешенной массы сателлита в относительном движении в область положительных значений инерционного момента, т.е. 
где
.
В качестве начальных значений для последующих циклов используются конечные значения предыдущего цикла, что вытекает из непрерывности процесса.
Полученные системы дифференциальных уравнений являются нелинейными и нестационарными. Рабочий процесс ИТВМ циклически повторяется. Задача оптимизации рабочего процесса сводится к нахождению минимума функционала
где i - передаточное отношение, 
- значение скорости ведомого маховика при переходе от участка разгона к участку совместного движения в текущем цикле рабочего процесса,
- значение скорости ведомого маховика при переходе от участка разгона к участку совместного движения в последующем цикле рабочего процесса.
Задача осложняется тем, что четыре такта цикла рабочего процесса, описываемые системами дифференциальных уравнений, зависят каждый от предыдущих. Рассматриваются два подхода к решению этой задачи. Один из них основан на идентификации неявных моделей технологических связей, описанный в работе [2], который позволяет избавиться от нахождения решения систем дифференциальных уравнений. Второй подход основан на получении приближенных аналитически решений систем (2)-(5) методом малого параметра (этот метод использовался для решения подобных систем в работе [3]) и последующим использованием полученных решений в задаче оптимизации.
Сравнение решений задачи оптимизации, полученной этими двумя методами, позволит выбрать из них лучший. В дальнейшем также планируется решение одним из выбранных методов задачи оптимизации рабочего процесса ИТВМ с учетом диссипативных потерь, упругих свойств вала реактора и характеристик двигателя внутреннего сгорания [1], математическая модель которого значительно сложнее.
Работа выполнена по плану Министерства образования и науки Российской Федерации.
Список литературы
- Баженов С.П. Бесступенчатые передачи тяговых и транспортных машин: Учеб. пособие /С.П. Баженов. - Липецк: Изд-во ЛГТУ, 2003. - 81 с.
- Блюмин С.Л. Оптимальное моделирование технологических связей: Учеб. пособие /С.Л. Блюмин, А.К. Погодаев, В.В. Барышев. - Липецк: Изд-во ЛГТУ, 1993. - 68 с.
- Леонов А.И. Инерционные автоматические трансформаторы вращающего момента /А.И. Леонов. - М.: Изд-во «Машиностроение», 1978. - 228 с.
Библиографическая ссылка
Баженов С.П., Блюмин С.Л., Галкин А.В. ЗАДАЧА ОПТИМИЗАЦИИ РАБОЧЕГО ПРОЦЕССА ИНЕРЦИОННОГО ТРАНСФОРМАТОРА ВРАЩАЮЩЕГО МОМЕНТА // Успехи современного естествознания. – 2006. – № 6. – С. 20-21;URL: https://natural-sciences.ru/ru/article/view?id=10497 (дата обращения: 19.04.2024).