Научный журнал
Успехи современного естествознания
ISSN 1681-7494
"Перечень" ВАК
ИФ РИНЦ = 1,002

Личный портфель

ПОСТРОЕНИЕ АДДИТИВНЫХ РАЗНОСТНЫХ СХЕМ В Р−МЕРНОМ  ПАРАЛЕЛЛЕПИПЕДЕ

Саиег Т. Х.

Для параболических уравнений с нелокальным источником в многомерной области Qt0= G x (0,t0] , рассмотрим задачу

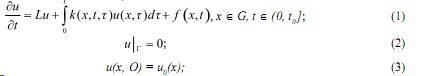
где

Г- граница области G.

Заменим многомерное уравнение (1) формально на цепочку одномерных уравнений теплопроводности:

Каждое из уравнений (4) заменим разностной схемой Pα υα = 0; α = 1,2, ... p или

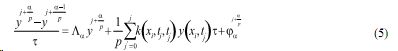
Так как система (5) аппроксимирует уравнение Pα υα = 0  в обычном смысле, то система (5) является аддитивной схемой.

Библиографическая ссылка

Саиег Т. Х. ПОСТРОЕНИЕ АДДИТИВНЫХ РАЗНОСТНЫХ СХЕМ В Р−МЕРНОМ  ПАРАЛЕЛЛЕПИПЕДЕ // Успехи современного естествознания. 2009. № 5. С. 84-84;
URL: https://natural-sciences.ru/ru/article/view?id=15690 (дата обращения: 12.07.2025).