В работах [1-2] изложены модернизированные уравнения Максвелла, получены их решения и проведены некоторые исследования. В новых уравнениях состояние ЭМП характеризуется теми же силовыми характеристиками поля, что и в традиционной модели. Для равномерного движения заряда со скоростью v = const в [3] приводятся следующие формулы:
E = Eφo - c-2v(vEφэ) +t(v
)Ejo, B = c-2 [vEφo], (1)
где Eφo - есть напряженность потенциального электрического поля, которая выражается через расчетный потенциал φo следующим образом
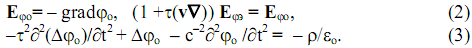
Здесь (3) волновое уравнение, τ - постоянная времени, - оператор набла.
Характеристики (1) зависят от запаздывающего момента времени. В традиционной теории переход к текущему моменту времени проводится на основе преобразований Лоренца
(4)
В новой электродинамике преобразования Лоренца в общем случае не работают. Поэтому нужно найти преобразования, которые бы позволили выразить (3) уравнением Пуассона
(5)
Рассмотрим случай равномерного движения заряда в той системе координат, в которой направление движения заряда q совпадает с ось ОХ, а начало координат находится в точке, которую заряд проходит в момент t=0. Тогда уравнение движения заряда описывается выражением R = Xex+Yey+Zez = r-vt (X=x-vt, Y=y, Z=z), где R расстояние от заряда до неподвижной точки М с координатами (x, y, z).
Выражаем приращения координат и времени в точке М через приращения проекций вектора R:
(6)
Тогда волновое уравнение (3) преобразуется к виду
(7)
Введем обозначения 
и обратные к ним операторы 
D2t =1, 
D2x =1, которые коммутируют между собой.
Запишем (7) в виде системы уравнений:
(8)
здесь 
- двухмерный оператор Лапласа. Уравнение (8) может иметь вид уравнения (5), если будет выполняться следующее равенство
(9)
Из (9) следует равенства операторов:
D
(10)
Представляя (9) в следующей форме 
, приходим к равенству операторов D2x(1- v2c-2j0-1 j0) = D2x¢, и далее переходим к следующему виду (1-v2c-2φ0-1 
φ0)D2x = 
. Применяя (10), получаем: 
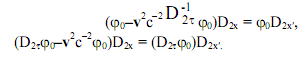(11)
Введем обозначение 
. (12)
Тогда из (11) с учетом (12) следуют: преобразования приращений координат
(13)
и преобразования координат соответственно
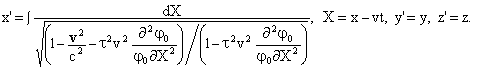(14)
Вывод. В новой электродинамике имеет место в общем случае трансцендентные преобразования координат. В области малых скоростей и в дали от заряда 
, поэтому преобразования (14) будут приближаться к преобразованиям Лоренца (4).
СПИСОК ЛИТЕРАТУРЫ:
- Меньшов Е.Н. Математическое моделирование электромагнитного поля: Деп. в ВИНИТИ от 25.10.2002, №1842 - В2002. - 9 с.
- Меньшов Е.Н. Фундаментальные свойства новых уравнений Максвелла. // Вестник УлГТУ.- 2004.- №4.- С.54-57.
- Меньшов Е.Н. Силы взаимодействия зарядов в классической электродинамике: Синтез, анализ, и диагностика электронных цепей: Тр. межд. конф. «КЛИН-2007» (г. Ульяновск, 17-18 мая 2007 г.).- Ульяновск: УлГТУ, 2007.- Том 3.- С.163-167.