Современные телекоммуникационные системы характеризуются тем, что потоки вызовов для новых видов связи отличаются от классических распределений потоков вызовов известных давно и широко используемых при анализе телефонных и телеграфных сообщений. Появление новых видов связи (передача данных в мобильных системах, IP-телефония и т.д.), требует изучения новых распределений потоков вызовов. Это необходимо для определения вероятностно-временных характеристик обслуживания данных видов связи. Кроме того, данные исследования важны при проектировании современных систем связи.
Методы анализа вероятностно-временных характеристик исследованы в работе /1/.
В данной статье рассмотрен один из возможных вариантов поступления входного потока вызовов, когда распределение вызовов подчиняется 
-распределению.
1. - распределение.
Пусть 
- независимые случайные величины, распределенные по одному и тому же стандартному нормальному закону
.
Закон распределения вероятностей неотрицательной случайной величины
носит название - распределение с числом степеней свободы n.
Плотность распределения интервалов между моментами поступления требований для - распределение определяется следующим образом:
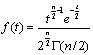
Найдём основные соотношения для вероятностно-временных характеристик согласно нового метода разработанного в литературе /1/.
Стационарная вероятность определяется следующим образом:
.
Следовательно, стационарная вероятность системы будет определена так:
.
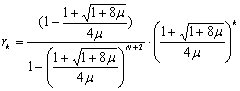Вероятность переполнения памяти накопительных устройств определяется, как вероятность того, что в системе находится N+1 требование:
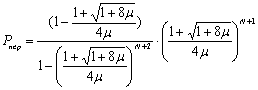
Среднее время пребывания требования в системе:
где 
- средняя длина очереди; λ- интенсивность поступления требований; μ- интенсивность обслуживания требований.
Среднее число вызовов ожидающих обслуживания для однолинейной системы 
.
,
.
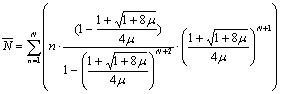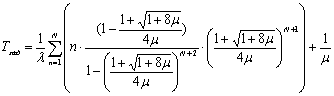СПИСОК ЛИТЕРАТУРЫ:
- Вероятностно ─ временные характеристики асинхронных сетей интегрального обслуживания: Научное издание / М.Н. Петров, Д.Ю. Пономарёв, Г.Х. Хачатрян, Г.Г. Яновский; Под ред. проф. М.Н. Петрова - Красноярск: НИИ СУВПТ, 2005.- 363 с. Второе издание, дополненное.