Обработка имеющихся экспериментальных данных проводится, как правило, по схеме "нелинейная физическая модель + линейная модель ошибки". В этом случае все экспериментальные величины описываются уравнением:
, (1)
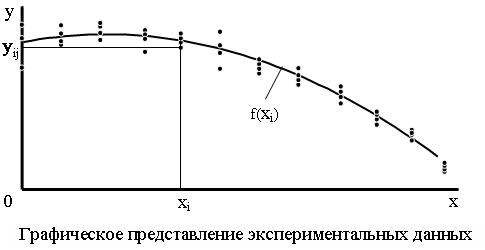
где: индекс i нумерует разные эксперименты (см. нижерасположенный рисунок), индекс j - номер экспериментальной точки внутри эксперимента, f - нелинейная функциональная зависимость между у и х, 
- погрешность измерения.
В научных исследованиях с многократно повторяющимися экспериментами, проводимыми в одинаковых условиях, наблюдается рассеивание экспериментальных данных из-за влияния на систему измерения непрогнозируемых физических факторов. Рассмотрим возможность оценки влияния случайной погрешности измерения на устойчивость экспериментальных данных с помощью дисперсионного анализа получаемых результатов.
Статистическую обработку результатов экспериментов методами дисперсионного анализа можно провести по схеме:
, (2)
где: 
- значение результативного признака Y, зафиксированного при j наблюдении на i уровне влияющего фактора; a - математическое ожидание признака Y всех измерений: a = 
, а 
; λi - генеральный эффект влияния Х на результативный признак Y, вызванный i уровнем влияющего фактора, 
, где ai средняя измерений на i-уровне; - случайный остаток, отражающий влияние на результативный признак всех случайных факторов, причём 
.
Результат каждого измерения содержит систематическую ошибку, учитываемую генеральным эффектом влияния Х на результативный признак Y, и случайную ошибку, характеризуемую . Методами дисперсионного анализа можно выявить статистическую устойчивость полученных результатов.
Для дисперсионного анализа данные измерений заносят в дисперсионную таблицу, с помощью которой проводят вычисления λi и по типовой схеме. Отношение λi будет характеризовать относительный уровень случайной погрешности измерения при проведении i-го эксперимента в j-м замере. Постоянство значений λi в разных экспериментах будет означать адекватность выбранной функциональной зависимости f на всём интервале изменения х.