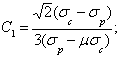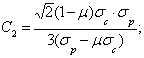Обобщенные критерии прочности не учитывают влияние на прочность упругих характеристик материала (например, коэффициент Пуассона m).
С учетом выше изложенного предлагаем искать критерий прочности в виде инвариантных по отношению к напряженному состоянию функций. При этом предполагаем, что сложное напряженное состояние будет эквивалентно простому растяжению при sr > 0 и простому сжатию при sr < 0:
|
t + C1sr £ C2 при sr > 0; t + C1 (-msr) £ C2 при sr < 0 |
 |
(1)
где t - касательные напряжения сдвига;
(-msr) - нормальные напряжения, соответствующие поперечным деформациям удлинения;
С1 и С2 - некоторые константы материала, определяемые при простом растяжении и сжатии.
В объеме напряженно-деформированного материала имеется площадка, у которой нормаль определяется направляющими косинусами в виде напряжений:
|
|
 |
(2)
где s1, s2, s3 - главные напряжения;
a1, a2, a3 - углы, образованные нормалью с соответствующими направлениями главных напряжений.
Нормальные напряжения на произвольной площадке определяются по формуле:
s = s1 cos2a1 + s2 cos2a2 + s3 cos2a3 (3)
После подстановки выражений (2) в формулу (3) находим необходимое выражение для результирующего нормального напряжения sr через главные напряжения, т.е.
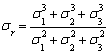(4)
При условии cosa1 = cosa2 = cosa3 = 1/ √3
(5)
Выражения для константы С1 и С2 получим из зависимости (1) с учетом формул (4) и (5) через предельные выражения для материала при одноосном растяжении (s1=sr, s2 = s3 =0) и при одноосном сжатии (s1 = s2 = 0, s3 = -sс), т.е.
|
|
|
(6)
Зависимости (1) с учетом выражений (6) будут иметь вид:
|
|
|
при sr > 0;
при sr £ 0
(7)
где 
- характеристика хрупкости материалов
Таким образом, мы получили искомый критерий прочности изотропных материалов с учетом их упругих свойств.