Scientific journal

Advances in current natural sciences

ISSN 1681-7494

"Перечень" ВАК

ИФ РИНЦ = 0,775

Рассмотрим численное решение полуэмпирического уравнения турбулентной диффузии:

  ,                     (1)

Для уравнения (1) должны быть заданы начальное условие

                   (2)

 и граничные условия:

       при z=0,                         (3)

если примесь полностью отражается подстилающей поверхностью;

 при z = 0                                    (4)

если примесь полностью поглощается подстилающей поверхностью

и

           (5)

Преобразуем полуэмпирическое уравнение (1) к следующему виду:

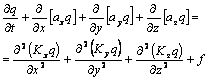,              (6)

, ,     (7)

Краевая задача (1) - (4) описывает два принципиально различных физических процесса, один из которых является процессом переноса субстанции с ее сохранением вдоль траектории под действием ветра и силы тяжести, и описывается задачей:

1) ,              (8)

, (9)

                           (10)

Второй физический процесс связан с диффузией примеси в процессе распространения и описывается задачей:

2) ,    (11)

,                 (12)

 при z=0,              (13)

       (14)

С помощью методов теории расщепления [2] задача (8) - (10) переноса примеси редуцируется в свою очередь на каждом интервале разбиения [t_i ,t_i+1 ], i = 0,1,..., временного интервала [t₀, T ], (причем временной интервал выбирается достаточно малым, чтобы свести до минимума возможную погрешность расщепления), к последовательному решению следующих задач:

1.1) перенос примеси вдоль оси ОХ:

,              (15)

, t Є [t_i, t_i+1 ]      (16)

        (17)

1.2) перенос примеси вдоль оси ОY:

,              (18)

, t Є [t_i, t_i+1 ]       (19)

       (20)

1.3.) перенос примеси вдоль оси ОZ:

,                        (21)

, t Є [t_i, t_i+1 ] (22)

, (23)

где - шаг дискретизации по времени.

Задача диффузии примеси (11) - (14) расщепляется на три последовательно решаемых задачи [2]:

2.1.) диффузия примеси вдоль оси ОХ:

 ,                      (24)

,                      (25)

 при z=0,                         (26)

        (27)

2.2.) диффузия примеси вдоль оси ОY:

   ,             (28)

  ,                         (29)

  при z=0,                     (30)

           (31)

2.3.) диффузия примеси вдоль оси ОZ:

   ,                   (32)

  ,                             (33)

  при z=0,                           (34)

             (35)

Решение краевых задач (15) - (35) осуществляется путем аппроксимации по формулам численного дифференцирования. Получающиеся при этом системы разностных уравнений решаются методом прогонки.

Рассмотрим численное решение первой задачи (15) - (17).

Запишем явную разностную схему:

  ,                     (36)

          (37)

Теперь запишем неявную разностную схему:

           (38)

Находя полусумму явной и неявной схем, получим схему Кранка-Николсона

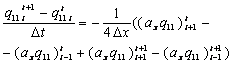        (39)

преобразуем (39):

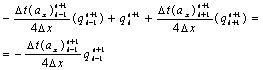(40)

Для решения системы (40) эффективен метод прогонки, суть которого в следующем:

Пусть  , C_i=1, , , тогда (40) запишем в виде :

  , (i=0,1,2,....m)         (41)

Проведем линейную интерполяцию q_i:

  , (i = 0,1,2,....m-1)              (42)

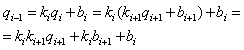     (43)

подставляя (42) и (43) в (41) получим:

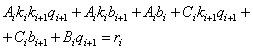
разделим 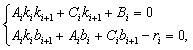(44):

                      (44)

где .

Отсюда находим k_i+1, b_i+1:

  ,                  (45)

Примем k₀=0 и b₀=0. Рассчитаем все значения k_i, b_i. Теперь можно выполнить обратную прогонку: по значениям k_i+1 , b_i+1 вычислим все значения q_i, положив q_m=0.

Аналогично можно найти решение остальных задач (18) - (35), определяющих распространение примеси вдоль осей OX и OZ, учитывая, что для уравнений второго порядка коэффициенты  будут иметь вид:

, ,

,

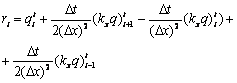Тогда приращение решения исходного уравнения (6) запишется как сумма приращений решений каждого из уравнений (15) - (35).

Данная задача сводится к выяснению вопроса о необходимости задания граничных условий для тех или иных случаев.

Таблица 1. Зависимость концентрации примеси от времени

Проанализируем приведенные в таблице 1 расчеты.

Пусть граничные условия не учитываются (рассматривается задача Коши (1) - (2)).

В течение времени 1с.-12с., с момента действия источника, наблюдается возрастание концентрации с 1,31 кг/м³ до 1,79 кг/м³ ( см. строку № 2 таблицы 1); в течение 12с. - 46с. - уменьшение с 0,62 кг/м³ - 3,62Е- 05 кг/м³ .

Аналогичные результаты изменения концентрации до 46с. имеем также в случае, когда граничные условия (3), (4) в задаче (1) - (4) учитываются.

После 46с., с момента действия источника, наблюдается значительное расхождение значений концентрации q для задач (1) - (2) и (1) - (4). Без учета граничных условий: с 3,62Е- 05 кг/м³ до 0 кг/м³ ,с учетом этих же условий: а) поглощение с 1,29Е- 05 кг/м³ до 0 кг/м³, б) отражение с 3,39Е- 05 кг/м³ до 0 кг/м³.

Программная реализация вышеописанного численного решения полуэмпирического уравнения турбулентной диффузии позволяет сделать вывод, что значения концентраций рассеяния примеси, полученные в результате расчетов в момент выброса ее в атмосферу, при задании граничных условий и без учета их имеют существенные различия.

СПИСОК ЛИТЕРАТУРЫ

1. Марчук Г. И. Математическое моделирование в проблеме окружающей среды. - М.: Наука, 1982. - 320 с.
2. Марчук Г. И. Методы расщепления. - М.: Наука, 1988. - 264 с.