В качестве модели телекоммуникационной сети удобно использовать сеть систем массового обслуживания (СМО), в которой каждый канал представляется двумя обслуживающими устройствами СМО, а узлы сети задают коммутационные матрицы для связи параметров потоков.
Входящими параметрами для узла являются интенсивности потоков λi,j, где i - индекс узла, откуда поступил поток, а j - индекс принимающего узла. Разные узлы имеют не одинаковое количество входов/выходов, обозначим их число через mi, где i - индекс узла. Также характеристикой узла являются плотности потоков после коммутации - ρi,kl, где i - индекс узла, а k, l - вход/выход через которые проходит поток(см. рис.1). Тогда интенсивность потока с i-го узла на j-ный можно представить в виде:
, (1)
где f(i1,i2) функция, которая задает распределение индексов входов/выходов, по сути, введена, чтобы не заострять внимание на выборе порядка их нумерации. Таким образом, было проведено суммирование по всем входам/выходам.
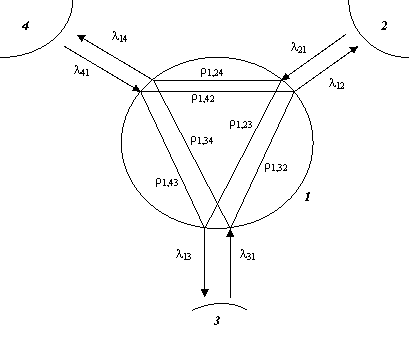
Рисунок 1. Характеристикой узла
Переходя к узлу в целом, данное уравнение можно представить в матричной форме, если ввести матрицу коммутации вида:
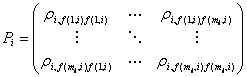
и вектор интенсивности потока для узла i:
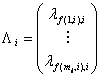
Тогда (1), с учетом всего узла, можно представить в виде:
.
Полная система для всех n узлов с mi входами/выходами будет описываться следующей системой линейных алгебраических уравнений:
, 
; 
(2)
или
, ; . (3)
Целью моделирования является исследование системы при различном поведении систем мониторинга СПД, которые вносят дополнительный поток данных в общий трафик сети. Так как данный поток никак не связан с общими потоками данных, то целесообразно ввести отдельные интенсивности для данного потока, т.е. необходима еще одна система уравнений, которая будет описывать распределение трафика системы мониторинга. В свою очередь задача мониторинга распадается на две составные части, это активный мониторинг некоторой контролирующей станцией и данные, которые посылают сами устройства СПД. Тогда полная интенсивность всех потоков:
,
где 
- интенсивность общего потока, 
- интенсивность потока создаваемого станцией мониторинга, 
- интенсивность потока событий от устройств:
, ;
, ;
, ;
Необходимо рассматривать задачу с нестационарными потоками. Ниже, непосредственное указание зависимости параметров потока от времени, в формулах может опускаться, но оно будет подразумеваться.
В качестве модели будем рассматривать Марковскую модель массового обслуживания. Воспользуемся «прямым» уравнением процесса рождения и гибели:
,
;
,
, 
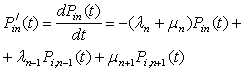(4)
Далее индекс i, который характеризует начальное состояние, опускается, но будет подразумеваться.
При анализе и решении этой задачи, параметры которой зависят от времени, удобно считать их зависимость периодической (подобная задача была решена в работе Clare A.B/: A Waiting Time Process of Markov Type, Ann. Math. Static., vol.24, pp.452-459,1956). Введем преобразование времени τ следующего вида:
.
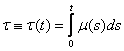Для упрощения вычислений воспользуемся масштабом времени τ:
, (5)
.
Подставляя (5) в (4) получим «прямое» уравнение процесса гибели и рождения с новой масштабной переменной τ:
,
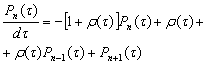, n>0. (6)
Пусть 
, n=0,1,..., тогда система (6) примет вид:
,
, n>0. (7)
Чтобы решить эту систему надо свести ее к дифференциальному уравнению в частных производных, используя метод производящих функций. Применяя производящую функцию
,
получаем уравнение:
. (8)
Дифференцируя Q(z,τ) по τ, беря z=τ и воспользовавшись уравнением для 
из (7) получаем граничные условия
. (9)
Из условия начального состояния системы находим, что 
, и пусть 
.
Решение задачи Коши для уравнения гиперболического типа находим методом Римана.
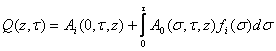. (10)
Где:
, , . . .;
,
;
, 
,
.
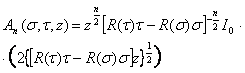
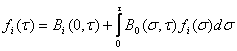Используя эти выражения, переходим от производящей функции Q(z,τ) к искомой:
. (11)
Зная условные вероятности того, что в момент времени τ в канале находится n пакетов (при условии, что в момент времени τ=0 было i пакетов) и плотность распределения длительности ожидания (n+1)-го пакета, несложно получить среднее время ожидания пакета в очереди.
Задача, выбора критерия оптимального мониторинга сетей передачи данных, сводится к максимизации частоты мониторинга fmon (для одной контролирующей станции). При этом должны выполняться следующие условия: условие «минимальных помех» (поток, создаваемый системой мониторинга, увеличивает среднее время ожидания не более чем на ζ) и условие «равномерности» (дисперсия среднего времени ожидания должна увеличиваться не более чем на η).
,
,, 
.
Надо заметить, что среднее время обслуживания Lq находится при условии отсутствия потока мониторинга, т.е. учитываем только λ(0), в то время, как Lqmon с учетом полного потока λ= λ(0)+λ(1)+λ(2). Аналогично для дисперсий Dq, Dqmon .