Предложены параллельные явные одношаговые методы первого, второго порядков, обеспечивающие возможность с минимальными вычислительными затратами интегрировать жесткие системы обыкновенных дифференциальных уравнений. В предлагаемых параллельных алгоритмах изменение величины шага построены на основе контроля точности и устойчивости численной схемы, а в неравенстве для контроля точности применяется оценка локальной ошибки метода.
В настоящее время одним из основных параметром, характеризующих эффективность использования вычислительной техники в науке и технологии, являются математические модели и численные методы, применяемые при создании программ для реализации исследований и расчетов по этим моделям. Моделирование процессов во многие важных приложениях приводит к необходимости численного решения задачи Коши для умеренно жестких систем обыкновенных дифференциальных уравнений [2, 3].
Рассматривается задача Коши для автономной системы обыкновенных дифференциаль ных уравнений первого порядка
y′ = f(y), y(t0) = y0, t0 ≤ t ≤ tk (1)
где y: [t0, tk] →RN, f: [t0, tk]× RN →RN, [t0, tk] -отрезок интегрирования. В предположении существования и единственности решения задачи (1) параллельная схема метода первого порядка с контролем точности для численного решения (1) в вычислительной системе из p процессоров, N > p и s = N/p, если N кратно p, или s = [N/p] + g, в противном случае, записывается в виде [1]
![]() (2)
(2)
где yjs(n) ∈ Comp(j), || δn ||= 0.5h || fn + 1 - fn || ≤ ε, 1 ≤ j ≤ p, (j-1)⋅s + 1 ≤ js ≤ j⋅ s, ||⋅|| - некоторая норма в RN , || δn ||- норма вектора локальной погрешности, fn + 1 и fn - значения правой части системы (1) соответственно в точках t n+1 и tn, ε требуемая точность. Параллельная схема второго порядка для численного решения (1) имеет вид
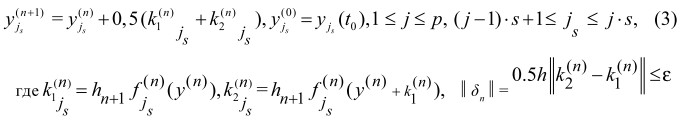 (3)
(3)
Неравенство для оценки устойчивости h | λmax |≤ D, где | λmax | -наибольшее собственное число якобиана, D - размер области устойчивости (для схемы (3) он равен 2). Выбор величины шага hn для схемы (2) определяется по формуле hn = qhn/1.1, где q = (ε /|| δn ||)1/2, а для схемы (3) по формуле hn = max(hn, qhn)/1.1, где q = (D / hn |λmax | )1/2 .
Укрупненная схема параллельных алгоритмов предложенных вычислительных схем (2), (3) состоит в следующем. Компоненты yjs(n) распределяются по p процессорам согласно блочной схеме распределения по s компонентов в каждом. Каждая задача Uj выполняется на proc(j), Uj ∈ proc(j). Proc(1) определяет значение шага hn и передает всем proc(j), используя коммуникационную операцию one-to- all. В каждом proc(j) вычисляются yjs(n), т.е. решается задача Uj, вычисляется значение локальной нормы || δn ||j и выполняется операция all-to-all. Для вычисления значений элементов fjs(y(n) ) вектора правой части разрабатывается отдель ная функция. Таким образом, общая схема параллельного алгоритма сводится к линейной форме и обеспечивается возможность анализа и оценки его эффективности алгоритма.
Алгоритмы реализованы в виде отдельных функций языка С и включены в комплекс программ, предназначенных для численного моделирования процессов, описываемых жесткими системами на многопроцессорных вычислительных системах кластерной архитектуры. Коммуникационные операции реализованы функциями библиотеки MPI.
Расчеты, выполняемые на 99-процессорном кластере ИВМ СО РАН [4] показали, что параллельные схемы (2), (3) применяться в случаях, когда расчеты требуется проводить с невысокой точностью - порядка 1 % и ниже.
Список литературы
- Ващенко Г.В., Новиков Е.А. Параллельная реализация явных методов типа Рунге-Кутты // Вестник КрасГАУ. - 2010 - №2 - С. 14-18.
- Новиков Е.А. Явные методы для жестких систем. - Новосибирск: Наука, 1997.
- Хайрер Э., Ваннер Г. Решение обыкновенных дифференциальных уравнений. Жесткие и дифференциально-алгебраические задачи. - М.: Мир, 1999.
- Исаев С.В., Малышев А.В., Шайдуров В.В. Развитие Красноярского центра параллельных вычислений // Вычислительные технологии. - 2006. - №11. - С. 28-33.



