В данной работе мы рассмотрим неопределенность вида 
для функции 
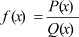. Для нахождения предела функции мы применяем метод преобразования, метод замены и определение бесконечно малых величин.
Пусть требуется найти предел дроби
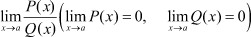(1)
где P(x) и Q(x) функции определенные в окрестности предельного аргумента a, но в самом предельном значении обращаются в ноль.
Теорема 1. Пусть число a для многочлена n-й степени P(x) = Pn(x) является k кратным решением, а для многочлена m-й степени Q(x) = Qn(x) является r кратным решением, тогда
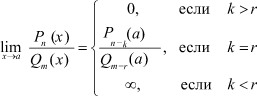(2)
где Pn-k(a) и Qm-r(a) значения соответствующих многочленов Pn-k(x) и Qm-r(x) в точке x = a.
Доказательство. Так как, число a является решением многочленов Pn(x) и Qm(x), то их в любое время можно представить в виде:
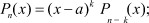
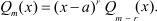
Тогда
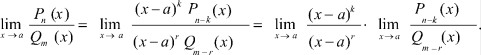(3)
Биномы (x - a)k и (x - a)r в окрестности точки x = a бесконечно малы, а их основания эквивалентные бесконечно малые.
Отсюда
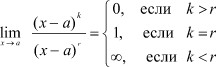
Полагаясь на последнее равенство, можно из (3) предела получить формулу (2).
Пример 1.
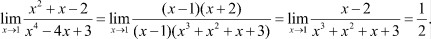
Пример 2.
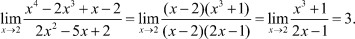
Список литературы
- Задачи и упражнения по математическому анализу / под ред. Б.П. Демидовича. - М.: Наука, 1978.
- Есмуханов М.Е. Предел функции в точке (казахском языке). - Алма-Ата, Изд-во «Мектеп», 1971.
- Запорожец Г.И. Руководство к решению задач по математическому анализу. - М., Высшая школа, 1966.