В работе предлагаются два основных решения для функции тока, при числах Фруда, меньших четырех, и больших четырех, которые определяются из общего решения двухмерной плановой задачи для бурного потока при свободном растекании. Новые решения лучше согласуются с экспериментом.
Интенсивное строительство автомобильных и железных дорог в России еще в XIX веке выдвинуло целый ряд проблемных вопросов по расчету отверстий малых мостов и дорожных труб. Так железнодорожная катастрофа, произошедшая в 1882 г. с многочисленными человеческими жертвами вблизи г. Тула была связана с разрушением из-за недостаточной водопропускной способности трубы под полотном дороги и размывом нижнего бьефа [1]. Обширные гидравлические исследования подобных конструкций были проведены в XX веке АО ВНИИВОДГЕО, ЦАГИ, КАДИ МГМИ, НИМИ, МИСИ [2, 3] и др. вузах и НИИ. Актуальны донные вопросы и для каналов обводнительно-оросительных систем, которые пересекаются с естественной гидрографической сетью в среднем через 7–8 км. Поэтому из подобных сооружений только на юге России более 20 тыс., находящихся на балансе Минсельхоза России и агропроизводителей.
Одним из приоритетных направлений по обеспечению экологической безопасности в настоящее время России является совершенствование существующих технологий в строительстве сооружений [4], которые подвергаются разрушению со стороны нижнего бьефа из-за недопустимого размыва крепления. Причиной разрушения крепления нижнего бьефа, в основном является неточный расчет параметров потока воды.
В [5] получено решение задачи свободного растекания потока по гладкому горизонтальному руслу для крайней линии тока, которое адекватно определяет зону повышенной нагрузки потока на боковое крепление, однако это решение не лишено недостатков. В предлагаемом решении параметры потока на выходе из трубы терпит разрыв модуль вектора скорости, а также направление вектора скорости. Кроме того, при числах Фруда, больших четырех, ухудшается адекватность полученного в [3] решения с экспериментальными данными.
Цель настоящей работы – получить решение задачи свободного растекания для функции тока, обладающее свойством непрерывности параметров потока на выходе из трубы и имеющее высокую адекватность с экспериментом.
В [5] было показано, что в случае растекания двухмерного стационарного потока без учета сил сопротивления в плоскости годографа скорости система уравнений движения бурного потока имеет вид:
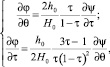(1)
где φ, ψ – соответственно потенциальная функция и функция тока; θ – угол наклона вектора скорости жидкой частицы к продольной оси симметрии потока – ОХ;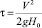 
– квадрат скоростного коэффициента; V – модуль вектора скорости жидкой частицы потока; h0 – глубина потока в некоторой характерной точке; V0 – модуль скорости в этой же точке; 
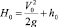– постоянная для всего потока; g – ускорение силы тяжести.
Система (1) совместно с граничными условиями позволяет ставить задачи плановой гидравлики в плоскости годографа скорости. При этом для решения конкретной задачи достаточно определить вид одной из функций φ = φ(τ, θ) или ψ = ψ(τ, θ), удовлетворяющей граничным условиям течения потока.
Рассмотрим задачу определения вида функции ψ = ψ(τ, θ) в случае свободного растекания бурного потока за безнапорным отверстием в широкое горизонтальное отводящее русло. В задаче свободного растекания бурного потока необходимо выполнение условия для граничной линии тока (рис. 1):
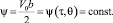(2)
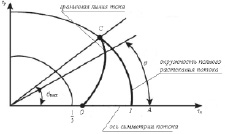
Рис. 1. Область течения потока в плоскости годографа скорости
Граничная линия тока «ОС» должна проходить через точку «О» с параметрами τ = τ0, θ = 0 и точку «С» с параметрами τ = 1, θ = θmax, таким образом,
ψ(τ, θ) = ψ(1, θmax). (3)
Угол «θmax» определяется из условия совпадения граничной линии тока с одной из характеристик потока, выходящей из точки τ = τ0, θ = 0, при τ → 1 [3]:
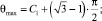
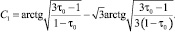(4)
Следует отметить, что условий (2), (3) для однозначного определения функции ψ(τ, θ) в задаче свободного растекания потока недостаточно, так как не определено физическое условие течения потока вдоль граничной линии тока.
Решение системы (1) для функции тока у потоков, имеющих продольную ось симметрии, согласно [7] записывается в виде:
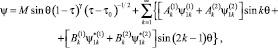(5)
где
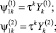
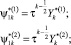
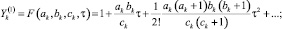
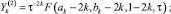
F(ak, bk, ck, τ) гипергеометрическая функция;
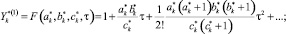
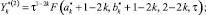
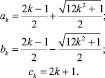
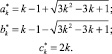
При этом считаем, что ck и 
в выражениях (5) не равны нулю или целому отрицательному числу; M,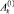 
, 
, 
, 
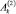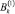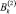– коэффициенты, подлежащие определению в результате решения задачи.
Первое слагаемое в выражении (5) необходимо для выполнения условия непрерывности по параметрам потока в окрестности выхода из отверстия. Величина определяется из условия достаточного затухания влияния первого слагаемого в выражении (5) по мере приближения τ к единице.
Решение вида (5) будем рассматривать такое, что для крайней линии тока (2) выполняется условие
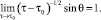(6)
Тогда постоянная M определяется из равенства:
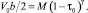(7)
Постоянные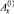 
, 
, 
, 
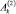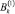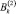определяются из условий:
1)
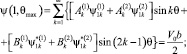(8)
2) функция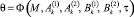 
(9)
вдоль граничной линии тока
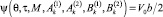
должна быть монотонно возрастающей по аргументу «τ» и максимальной в зависимости от коэффициентов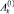 
, 
, 
, 
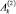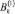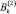при каждом фиксированном «τ» [5]. Свойство монотонности следует из основных свойств бурного свободнорастекающегося потока. Оптимум по углу «θ» следует из законов оптимальности в задачах, имеющих какую-либо свободу выбора, а также совпадения результатов моделирования, эксперимента и натурных исследований.
Решение задачи свободного растекания бурного открытого водного потока начнем с определения постоянных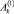 
, 
, 
, 
.
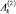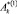Рассмотрим вначале самый простой случай решения задачи при k = 1 и выборе решения (первое слагаемое в ряде (5) для простоты можно опустить)
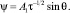(10)
В этом случае исследования проводятся вдоль крайней линии тока, начиная не с точки (τ = τ0, θ = 0) а с разрывом параметров течения на выходе из трубы, т.е. с точки K(τ = τK, θ = θK) (рис. 2).
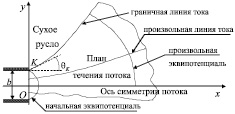
Рис. 2. План растекания потока с разрывом параметров на выходе из трубы
При γ = 11 в решении (5) в пределе выполняется и условие
ψ(τ0, 0) = V0b/2
и практически возможен на малом расстоянии по «х»: x/b < 0,1 рост угла θ от нуля до конечного θk, поэтому выбор решения в виде (10) оправдан. Вид решения (10) имеет следующее обоснование:
при 0 < θ < π/2 функция f1(θ) = sin θ монотонно возрастающая; функция f2(τ) = τ1/2 также монотонно возрастает при τK ≤ τ < 1
Таким образом, отношение этих функций может быть постоянным при изменении самих аргументов τ и θ.
Постоянная A1 определяется из условия:
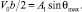(11)
В случае, когда число постоянных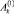 
, 
, 
, 
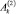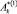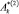в выражениях (5) равно двум, то возможен вариант:
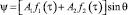. (12)
В этом случае имеем:
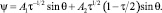(13)
Вдоль крайней линии тока при τ = 1, θ = θmax поэтому из (13) следует равенство:
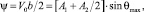(14)
следовательно:
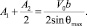(15)
Будем полагать, что коэффициенты A1 и A2 являются неотрицательными величинами. Считаем функцию
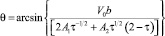(16)
монотонно возрастающей и доставляющей максимум при любых τ из области изменения [τ0; 1].
На базе математического пакета «Mathcad, version 11.0»была разработана программа, определяющая оптимальные значения коэффициентов A1, A2. На рис. 3 показано сравнение функций угла растекания потока (17) при значениях τ0 = 0,5, параметр A2 определялся из зависимости (15), значение параметра A1 равно
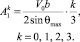(17)
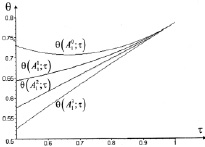
Рис. 3. Графики угла растекания потока при τ0 = 0,5 и различных значениях A1A1
Из рисунка (3) нетрудно видеть, что условию наибольшего растекания потока и его монотонности по τ соответствует функция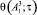 
, то есть функция
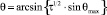(18)
Результаты моделирования сравнивались с результатами экспериментов. Это сравнение позволило сформулировать следующее утверждение: найденные постоянные
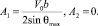(19)
в выражении (5) доставляют максимум функции
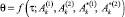(20)
для соответствующих значений «τ», τ ∈ [τ0; 1] при этом функция (20) является монотонно возрастающей по τ и удовлетворяет условию:
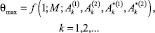(21)
Высокую степень адекватности по параметрам потока в окрестности выхода потока из трубы до расширения потока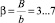 
дает модель по формуле (12) с постоянными (19)
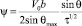(22)
при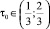 
.
Последующее решение задачи в физической плоскости сводится к использованию зависимости (12) с учетом того, что вдоль каждой линии тока dψ ≡ 0, соответственно вдоль эквипотенциали dφ ≡ 0 и интегрированию получаемых уравнений.
Для случая (12) выражение для потенциальной функции имеет следующий вид:
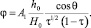(23)
В этом случае задача по определению параметров потока в точке пересечения произвольной линии тока с произвольной эквипотенциалью сводится к поиску решений системы:
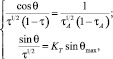(24)
где A – произвольная точка оси симметрии потока, через которую проходит эквипотенциаль.
Пусть теперь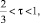 
тогда функция 
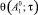является монотонно возрастающей (рис. 3), соответственно постоянные определяются по формулам
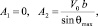(25)
которые в выражении (5) доставляют максимум для функции (20). Функция тока в этом случае имеет вид
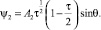(26)
Потенциальная функция, соответствующая решению с константами (25), определяется из системы (1) при известной функции тока (26)
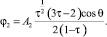(27)
Для оценки степени адекватности потока приведем результаты сравнения экспериментальных исследований с модельными (по методу автора и известных исследователей в области растекания плановых потоков).
Параметры потока на выходе из трубы
b = 16 см; V0 = 148 см/с;
h0 = 148 см; Fr0 = 2/397.
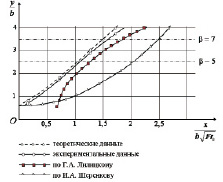
Рис. 4. Сравнение экспериментальной линии тока с графиками, построенными различными методами
Из результатов сравнения относительного рассогласования ординат крайней линии тока в теории и эксперименте видно, что при относительном расширении β = 7 погрешность не превышает 7 %, при этом рассогласование эксперимента с кривой по Г.А. Лилицкому превышает 15 %, а с кривой по И.А. Шеренкову – 40 %.
Выводы по работе
1. Пользуясь основными свойствами бурных потоков, авторы получили модели растекания потока при 1< Fr0 < 4 и Fr0 ≥ 4 что повышает ее адекватность по геометрии растекания потока и по определению его параметров.
2. Полученные решения двухмерной плановой задачи обладают свойством непрерывности по параметрам потока на выходе из трубы в нижний бьеф.