Практически все природные минералы содержат в кристаллической структуре точечные дефекты различной природы, а, следовательно, химический состав их не является стехиометрическим Наличие точечных дефектов в структуре, несомненно, отражается в типоморфизме минералов.
В качестве примера рассмотрим сульфиды железа Fe1-nS (0 < n < 0,125), обладающие различным типом сверхструктур в зависимости от плотности вакансий в структуре. Очевидно, что для различного типа сверхструктур, обусловленные катионными вакансиями, в кристаллической матрице могут реализовываться различные обменные взаимодействия на подрешетках, а это, в свою очередь, будет проявляться в различных типах зависимости результирующего магнитного момента (и, следовательно, намагниченности) от температуры [1, 3, 4, 7, 10]. Например, в зависимости от химического состава и температуры, эти сульфиды могут переходить из антиферромагнитного состояния в ферримагнитное и наоборот [3, 4]. Ферримагнетизм сульфидов железа Fe1-nS в интервале составов (0,09 < n < 0,125) объясняется неодинаковой плотностью катионных вакансий на подрешетках с ферромагнитным спиновым упорядочением [4, 10]. Экспериментально доказано, что намагниченность сульфидов железа может обращаться в ноль ниже температуры Нееля [3, 4]. Отметим, что температура Нееля для всего интервала составов Fe1-n S (0 < n < 0,125) равна 320 °С [1, 4, 10]. Очевидно, что тип распределения вакансий может существенно влиять на результирующую намагниченность, а, следовательно, и на магнитные свойства таких соединений [3, 6, 10]. Например, в ряде случаев резкий спад намагниченности при нагревании в вакууме сульфидов железа объясняется разупорядочением вакансий, однако это предположение не находит экспериментального подтверждения [2, 4, 7]. Не ясным остается и факт спада намагниченности до нуля при температуре, ниже температуры Неля. Эта температура зависит от химического состава и с увеличением плотности вакансий в структуре возрастает [4].
Цель исследования:
а) на основе анализа s-d обменного взаимодействия в структурах типа NiAs, в которых часть катионных позиций вакантны, предложить модель поведения намагниченности нестехиометрических ферримагнетиков в зависимости от характера распределения вакансий в структуре;
б) в рамках предложенной модели дать объяснение наблюдаемым различным аномалиям на термокривых намагниченности нестехиометрических пирротинов.
Материал и методы исследования
Исследовались синтетические пирротины, подробно описанные в работе [4]. Спектр ЯГР ферримагнитного пирротина (рис. 1) состоит из трех разрешенных секступлетов [4], соответствующих значениям напряженности магнитных полей на ядрах подрешеток, равных 24032, 20212, 18064 А/м.
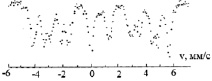
Рис. 1. Спектр ЯГР ферримагнитного пирротина состава FeS1,14
Эти значения напряженностей локальных магнитных полей соответствуют позициям ионов железа без вакансий, с двумя вакансиями и четырьмя вакансиями во второй координационной сфере соответственно. Такие позиции ионов железа могут возникнуть только в том случае, если катионные вакансии расположены преимущественно в четных или нечетных базисных плоскостях [4].
Такой характер распределение вакансий соответствует структурному переходу В8–С6 в промежуточной стадии. Расчет заселенности кристаллографических позиций в такой структуре дает следующие значения: N0 = 0,47; N1 = 0; N2 = 0,39; N3 = 0; N4 = 0,23. Узлы кристаллической структуры при случайном законе распределения вакансий имеют заселенности: N0 = 0,21; N1 = 0,3; N2 = 0,31; N3 = 0,14; N4 = 0,05 (N0, N1, N2, N3, N4 – вероятность заселенности позиций ионами железа в узлах кристаллической структуры без вакансий, с одной вакансией, двумя, тремя и четырьмя вакансиями во второй координационной сфере соответственно). Эти факты заставляют внести коррективы в модель двухподрешеточного ферримагнетика. Действительно, катионы в кристаллической структуре ферримагнитного пирротина находятся в четырех различных позициях с разными значениями напряженности магнитного поля, а, следовательно, с различными значениями обменного взаимодействия. В случае пирротина, не содержащего вакансий в кристаллической структуре (троилит), напряженность магнитных полей на ядрах двух магнитных подрешеток одинакова и равна 24032 А/м. Между этими магнитными подрешетками реализуется антиферромагнитное взаимодействие, а все ионы железа находятся в позиции без вакансий во второй координационной сфере. Очевидно, что заселенность такой позиции N0 = 1,00.
С учетом изложенного выше, необходимо произвести расчет результирующей намагниченности для модели не двух-, а четырех-подрешеточного ферримагнетика. Расчет для двух – подрешеточного ферримагнетика предложен Тябликовым [5] и успешно был применен для объяснения аномального поведения термокривых намагниченности пирротинов различного состава [2, 8, 9]. Для четырех – подрешеточного ферримагнетика алгоритм вывода расчетных формул не изменится, однако усложнится непосредственный вывод формул. По этой причине, в представленном изложении будут показаны только ключевые моменты вывода формулы, необходимые для понимания конечных результатов вычислений.
Для анализа поведения намагниченности рассмотрим отдельно обменное взаимодействие между катионами в нестехиометрическом ферримагнетике. В данном случае необходимо учитывать два фактора: в какой плоскости находится атом и вторую координационную сферу кристаллической структуры данного атома. Следовательно, надо рассмотреть, по крайней мере, четыре типа обменного взаимодействия.
Обозначим через f, g, k, l узлы первой, второй, третьей и четвертой подрешетки; величины, относящиеся к первой, второй, третьей и четвертой подрешеткам, – 1, 2, 3 и 4; Ni , Si , μi – число атомов в подрешетке, величину спина и магнитный момент атома сорта i.
В общем случае
N1 ≠ N2 ≠ N3 ≠ N4; S1 ≠ S2 ≠ S3 ≠ S4, μ1 ≠ μ2 ≠ μ3 ≠ μ4
т.е. магнитные моменты подрешеток различны.
Запишем гамильтониан системы в виде [88, 90]
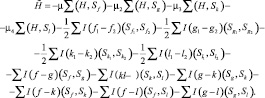
где Sf, Sg, Sk, Sl – спиновые операторы атомов первой, второй, третьей, четвертой подрешеток.
Принимая во внимание условие минимума свободной энергии:
F = –ϑln Q,
где Q – статистическая сумма, равная
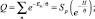
здесь J – модуль канонического распределения, равный kT; En – собственные значения гамильтониана H.
Перейдя к операторам
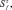
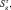
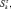
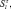
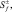
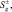
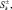
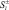
и применяя представления Гольштейна–Примакова–Изюмова спиновых операторов через операторы вторичного квантования, получим
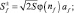
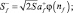
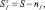
где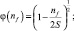 
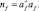
Операторы a+, a – удовлетворяют бозевским перестановочным соотношениям.
Предположив, что в каждой из подрешеток спины ориентированы параллельно друг другу, получим систему уравнений:
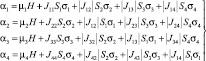
Система уравнений – это и есть искомые уравнения молекулярного поля для четырех – подрешеточного изотропного ферримагнетика:
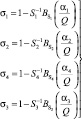
Результирующая намагниченность определяется уравнением:
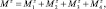
где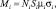 
σi – относительная намагниченность на один узел в подрешетке i.
Результаты теоретического моделирования и обсуждение их графического представления
Как уже отмечалось, величина магнитного момента определяется плотностью вакансий на каждой из подрешеток. Хотя модель и является общей для нестехиометрических ферримагнетиков, однако в случае конкретных вычислений привязка осуществляется к структуре нестехиометрического пирротина. Этим и объясняется расчетные величины интегралов обменного взаимодействия, базирующих на том факте, что температура Нееля для всего интервала составов Fe1-n S (0 < n < 0,125) равна 320 °С. Ясно, что в других соединениях эти параметры (также как и температура Неля) будут иметь иные численные значения.
При объяснении кривой относительной намагниченности J/Jo(T) 4-подрешеточного ферримагнетика уточним тот факт, что результирующий магнитный момент всех подрешеток (∑Μi) отличен от нуля только в том случае, если плотность вакансий на подрешетках различна. В противном случае суммарный магнитный момент его равен нулю (а образец, следовательно, будет проявлять свойства антиферромагнетика). Для определенности будем считать, что плотность вакансий в четных базисных плоскостях больше, но различно для каждой из подрешеток. Этот случай соответствует частичному упорядочению вакансий в четных базисных плоскостях.
Проведем анализ результатов расчета. На рис. 2 представлены типичные кривые зависимости результирующей относительной намагниченности ферримагнетика с различным обменным взаимодействием на подрешетках. Заметим, что расчеты произведены для значения обменного взаимодействия между подрешетками, равного J12 = J21 = 6,11∙10–21 Дж. В самих подрешетках значение обменного интеграла изменялось от J11 = 8,41∙10–21 Дж до J22 = 4,19∙10–21 Дж в зависимости от плотности вакансий на них. Численное значение интеграла получено по данным рентгеноструктурного анализа, исследования термомагнитных свойств пирротинов и мессбауэровской спектроскопии. Величина обменные взаимодействия в подрешетках может изменяться в допустимых пределах. Эти пределы определяются постоянством суммарной магнитной энергии ферримагнетика, численное значение которой связан с температурой магнитного перехода «порядок – беспорядок». Температура этого перехода всех подрешеток вследствие наличия обмена между ними должна быть одинаковой.
Из анализа кривых рис. 2 (Мр) видно, что результирующий момент может возрастать с увеличением температуры до некоторого значения, как показывает кривая 1. При определенных соотношениях обменных интегралов результирующая кривая относительной намагниченности может иметь обычный Вейсcовский характер (рис. 2, кривая 2) или спадать с увеличением температуры до нуля при Т < TN, как показывает кривая 5 на рис. 2. Как показывают расчеты, результирующая кривая может также иметь резкий спад намагниченности в определенной области температур (кривая 3). Особенности такой кривой намагниченности – это наличие достаточно пологого участка вблизи температуры Кюри. Практически намагниченность может обращаться в нуль ниже температуры Кюри (рис. 2, кривая 4). Возможна даже такая ситуация, когда магнитные моменты всех подрешеток окажутся равными при некоторой температуре, меньшей температуры Кюри (кривая 5). Расчеты показывают, что в подобном случае при дальнейшем увеличении температуры может наблюдаться увеличение результирующей намагниченности. На кривой появится своеобразный λ – пик намагниченности (рис. 2, кривая 5), природа которого не связана с изменением упорядочения катионных вакансий, а определяется только соотношением величин обменных интегралов в подрешетках.
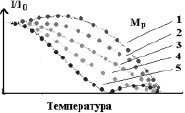
Рис. 2. Расчетные кривые зависимости относительной намагниченности от температуры нестехиометрических ферримагнетиков, полученные в результате компьютерного моделирования их результирующего магнитного момента Мр. Кривые 5, 4, 3, 2, 1 соответствуют процентному содержанию вакансий в четных базисных плоскостях 9,9; 10,7; 11,6; 12,5 и 13,7 % соответственно
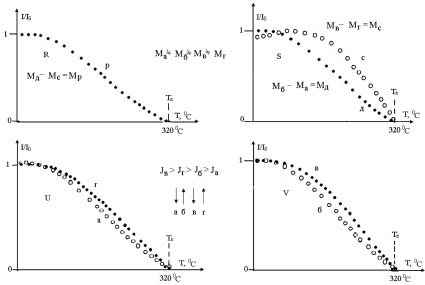
Рис. 3. Зависимость относительной намагниченности I/I0 каждой из четырех подрешеток – в, б (V) и а, г (U). Результирующая намагниченность двух подрешеток с большими (кривая с) и с меньшими (кривая д) интегралами обменного взаимодействия представлены на рис. S. Результирующая намагниченность четырехподрешеточного ферримагнетика представлена кривой р – рис. R
Между подрешетками а, б, в, г реализуется, как и показано на рисунке, антиферромагнитное спиновое упорядочение. Jа, Jб, Jв, Jг – интегралы обменных взаимодействий в подрешетках а, б, в, г соответственно; Ма, Мб, Мв, Мг – магнитные моменты этих подрешеток в каждой из которых реализуется ферромагнитное спиновое упорядочение
Проведем детальный анализ поведения намагниченности одной из серии кривых, представленных на рис. 2. Выберем, например, кривую 4. На рис. 3 отражено поведение намагниченности отдельно для каждой из четырех подрешеток (рис. 2, 3 V и U), а также результирующая намагниченность ферримагнетика (рис. 2, 3 R). Поскольку между базисными плоскостями реализуется антиферромагнитное спиновое упорядочение, то на рис. 2, 3 S отдельно показаны кривые намагниченности для двух пар соседних базисных плоскостей, но с различным обменным взаимодействием внутри каждой плоскости. Следует отметить, что величина магнитного момента каждой из подрешеток определяется плотностью катионных вакансий в ней – магнитный момент подрешетки уменьшается при увеличении плотности вакансий.
Интеграл обменного взаимодействия связан с числом вакансий во второй координационной сфере каждой позиции иона железа на магнитных подрешетках. Как уже отмечалось, минимальное значение обменный интеграл (Jа) принимает для позиций с 4 вакансиями во второй координационной сфере. Заселенность таких позиций достаточно мала (N4 не превышает значение 0,23), поэтому и Ма имеет минимальное значение. Следовательно, Мд максимален по величине.
Выводы
На основании теоретических вычислений и экспериментальных данных установлено, что:
а) двухподрешеточный ферримагнетик, содержащий в структуре катионные вакансий, должен рассматриваться, при определенном типе распределения вакансий в структуре, как ферримагнетик с четырьмя магнитными подрешетками;
б) на основе квантово-механических расчетов удельной намагниченности каждой из магнитных подрешеток представлено поведение кривой относительной намагниченности – I/I0 (T) образца;
в) в ряде случаях аномальное поведение намагниченности минералов типа пирротина, а именно:
• плавный рост намагниченности с возрастанием температуры в широком интервале температур;
• презкий спад намагниченности практически до нуля при температурах, ниже температуры Нееля;
• презкий рост намагниченности с повышением температуры вблизи температуры Нееля – можно объяснить в рамках модели 4х – подрешеточного ферримагнетика.