В пространстве Cn+1 комплексных переменных x1, x2, ..., xn+1 рассмотрим дифференциальное уравнение порядка 2p вида
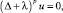(1)
где Δ – оператор Лапласа
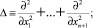
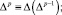
p ∈ N, p ≥ 2, λ = const.
Точку (x1, x2, ..., xn+1) пространства Cn+1 обозначим для краткости (X, z), где X = (x1, x2, ..., xn), z = xn+1.
Для уравнения (1) рассмотрим задачу Коши в следующей постановке: найти голоморфное решение u уравнения (1), удовлетворяющее начальным условиям:
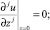j = 0, 1, ..., 2p 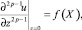– 2,
(2)
где f(X) – функция, голоморфная в некоторой области голоморфности D пространства Cn комплексных переменных x1, x2, ..., xn.
Теорема. Если функция v(X, z) является решением полигармонического уравнения Δpv(X, z) = 0, удовлетворяющим начальным условиям вида (2), то решение u(X, z) задачи Коши (1), (2) описывается формулой
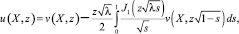(3)
где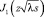 
–функция Бесселя.