Выполнение контрольно-обучающих мероприятий в современном вузе обязательно включает прохождение интернет-экзамена по различным дисциплинам. Особенность системы тестовых заданий по математике [1] состоит в том, что она охватывает многообразие учебных тем, поэтому подготовка к компьютерному тестированию выступает как трудоемкий процесс, который требует запоминания большого количества формул и вычислительных приемов. Обычное повторение ранее изученного материала и анализ решения типовых задач во время подготовки к ответственному испытанию не всегда приводит к успешному достижению желаемого результата на контрольной диагностике математических знаний и умений. Построение технологической карты (ТК), обобщающей учебную информацию, освоение которой подвергается аттестации, оказывает положительное воздействие на активизацию самостоятельной работы студентов.
Подлежащие диагностике знания и умения по дисциплине «Математика» в рамках основной образовательной программы по специальности или направлению подготовки фиксируются в специальном документе (кодификаторе) [2]. В нем представлена система элементов содержания дисциплины с разбиением на дидактические единицы (ДЭ) и контролируемые учебные элементы (КУЭ). Структура ТК, предназначенная для обобщения учебного материала по математике, может включать следующие компоненты: 1) название ДЭ и темы; 2) содержание КУЭ; 3) краткий обзор учебного материала (формулы, определения понятий, теоремы, графики функций, схемы, рисунки); 4) систему учебных заданий; 5) решение учебных заданий (графические модели, запись начальных данных, причинно-следственные связи). Составление системы учебных задач осуществляется на основе анализа протоколов ответов тестируемых. Пример ТК по теме «Прямая на плоскости», направленной на обобщение знаний и умений, представлен в таблице.
Технологическая карта по дисциплине «Математика»
|
ДЭ «Аналитическая геометрия» |
Тема «Прямая на плоскости» |
|
КУЭ |
Учебные задания |
|
Знание типов уравнений прямой на плоскости, формул вычисления угла между прямыми и расстояния от точки до прямой, условия параллельности и перпендикулярности прямых и умение использовать их при решении задач |
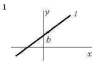
1. Прямая отсекает на оси Oy отрезок b = 3 и имеет угловой коэффициент 2/3. Тогда ее уравнение имеет вид …… Варианты ответа: 1) 3у – 2х – 9 = 0; 2) у + х – 3 = 0; 3) 3у – 2х + 6 = 0; 4) 2у – 3х – 6 = 0. 2. Прямая проходит через точку М (2; 1) перпендикулярно прямой 2х + 3у + 4 = 0. Тогда общее уравнение этой прямой имеет вид …. Варианты ответа: 1) 3х – 2у – 4 = 0; 2) 2х + 3у + 11 = 0; 3) 2х + 3у – 7 = 0; 4) 3х – 2у – 4 = 0.
3. Уравнение прямой, проходящей через точку пересечения прямых Варианты ответа: 1) 4х + 5у – 21 = 0; 2) 5х – 4у – 16 = 0; 3) 5х – 4у + 16 = 0; 4) 4х + 5у + 21 = 0.
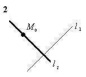
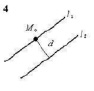
4. Расстояние между прямыми Варианты ответа: 1) 2,5; 2) 5; 3) 0,25; 4) 1,5.
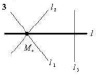
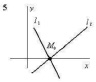
5. Прямые Варианты ответа: 1) (2; 0); 2) (7; 0); 3) (9; 0); 4) (16; 0) |
|
Краткий обзор учебного материала [3] Типы уравнений прямой на плоскости 1) y = kx + b – уравнение прямой с угловым коэффициентом; 2) Ax + By + C = 0 – общее уравнение прямой; 3) y – y0 = k(x – x0) – уравнение прямой, проходящей через данную точку в данном направлении;
4)
5) 6) A(x – x0) + B(y – y0) = 0 – уравнение прямой, проходящей через данную точку перпендикулярно данному вектору |
|
|
Угол между прямыми на плоскости
|
|
|
Условия параллельности прямых
|
|
|
Условия перпендикулярности прямых
|
|
|
Расстояние от точки до прямой
|
|
Решение учебных заданий |
||
|
Графические модели |
Известные и искомые величины |
Причинно-следственные связи |
|
|
Дано: Найти А, В, С. |
y = kx + b → Ax + By + C = 0,
|
|
|
Дано: x0 = 2, у0 = 1, l1: 2х + 3у + 4 = 0,
Найти А2, В2, С2. |
|
|
|
Дано:
Найти А, В, С. |
|
|
|
Дано:
Найти d. |
|
|
|
Дано:
l2: mx + (2m-1)y – 9 = 0; M0(x0; 0). Найти x0. |
M0(x0; 0) ∊ l1, M0(x0; 0) ∊ l2; ⇒
⇒
⇒ |
Важным компонентов при построении ТК является визуализация условий задачи с помощью графических моделей, так как они позволяют выявить характерные особенности взаимосвязей известных величин с искомыми и »увидеть» путь движения к поставленной цели. Большую помощь при составлении ТК оказывает работающий в online режиме тренажер [1], обеспечивающий подготовку к прохождению интернет-экзамена. Он обладает особенностью, состоящей в том, что сообщает тестируемому в его протоколе ответов правильные решения задач, с которыми тот не справился. Накопление протоколов ответов неудачных сеансов тестирования вооружает обучаемого хорошей базой материалов для всестороннего анализа причинно-следственных связей КУЭ.
Применение представленного варианта обобщения учебного материала помогает целенаправленно концентрировать диагностируемые математические знания и умения, своевременно раскрывать в них пробелы, анализировать допущенные ошибки, оценивать оптимальность процесса решения.




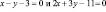 , перпендикулярно прямой
, перпендикулярно прямой 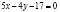 имеет вид …..
имеет вид …..
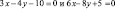 равно …
равно …
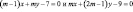 пересекаются в точке, лежащей на оси абсцисс, имеющей координаты …
пересекаются в точке, лежащей на оси абсцисс, имеющей координаты …
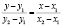 – уравнение прямой, проходящей через две точки;
– уравнение прямой, проходящей через две точки;
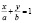 – уравнение прямой в отрезках;
– уравнение прямой в отрезках;
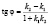
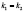
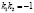
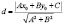
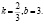
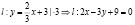
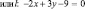 .
.
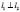 .
.
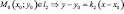 ;
;
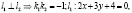
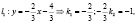
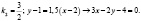
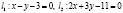 ,
,
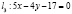 ,
,
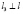 .
.
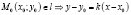 ;
;
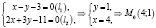 ;
;
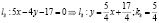 ;
;
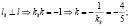
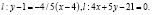
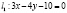 ,
,
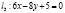 ,
,
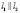 .
.
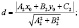
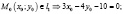
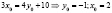 ;
;
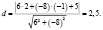
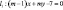 ;
;
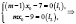
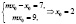 .
.