Решение многих практически важных задач, возникающих при исследовании процессов фильтрации жидкости в трещиновато-пористых средах [1], [9], движения подземных вод со свободной поверхностью в многослойных средах [10] связано с необходимостью исследования нелокальных задач для псевдопараболических уравнений [2].
Для модельного псевдопараболического уравнения А.М. Нахушевым в [8] была сформулирована краевая задача с нелокальным условием.
Цель исследования: доказать существование и единственность решения нелокальной задачи для псевдопараболического уравнения третьего порядка.
Постановка задачи. Пусть
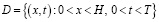
конечная область плоскости переменных xyt 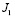 интервал
интервал 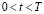 прямой
прямой 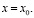 Для общего псевдопараболического уравнения
Для общего псевдопараболического уравнения
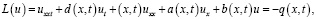
в области D ставится задача.
Задача. Найти регулярное в области 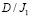 решение
решение 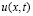 уравнения (1) из класса
уравнения (1) из класса 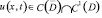 удовлетворяющее условиям:
удовлетворяющее условиям:
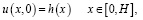 (2)
(2)
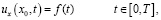 (3)
(3)
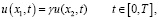 (4)
(4)
где 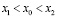 – произвольно фиксированные точки из интервала
– произвольно фиксированные точки из интервала 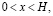 γ = const f(t) и h(x) непрерывные функции.
γ = const f(t) и h(x) непрерывные функции.
Справедлива следующая теорема.
Теорема: Если коэффициенты уравнения (1) и заданные функции удовлетворяют условиям
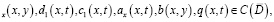
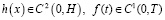
а также
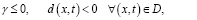
то задача (1)-(4) разрешима и притом единственным образом.
Доказательство. Справедливость теоремы докажем методом функции Римана [8].
В области
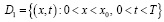
рассмотрим характеристическую задачу Гурса [3]
 (5)
(5)
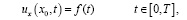
 (7)
(7)
для уравнения (1), где 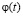 – неизвестная пока функция из класса
– неизвестная пока функция из класса 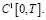 Пусть
Пусть 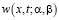 – функция Римана, введенная в [8], которая однозначно определяется следующими требованиями:
– функция Римана, введенная в [8], которая однозначно определяется следующими требованиями:
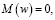
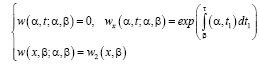
где 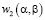 – решение следующей задачи:
– решение следующей задачи:
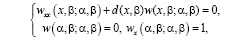
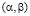 – произвольная точка области
– произвольная точка области 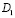 .
.
Единственность и существование функции Римана 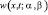 доказывается методом редукции к нагруженным интегро-дифференциальным уравнениям [7].
доказывается методом редукции к нагруженным интегро-дифференциальным уравнениям [7].
Интегрируя тождество
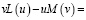
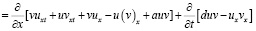 (8)
(8)
по области 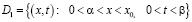 с учетом свойств функции Римана
с учетом свойств функции Римана 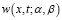 и условий (5) – (7), получим
и условий (5) – (7), получим
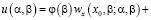
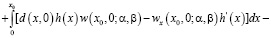
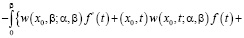
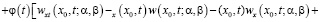
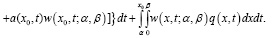 (9)
(9)
Формула (9) дает явное представление решения задачи Гурса (1), (5)-(7).
Для нахождения неизвестной функции 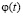 по аналогичной схеме в
по аналогичной схеме в 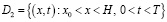 рассмотрим характеристическую задачу Гурса
рассмотрим характеристическую задачу Гурса
 (10)
(10)
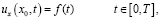 (11)
(11)
 (12)
(12)
для уравнения (1).
Пусть 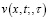 – функция Римана, удовлетворяющая условиям:
– функция Римана, удовлетворяющая условиям:
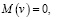
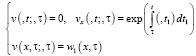
где 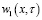 – решение задачи [5]:
– решение задачи [5]:
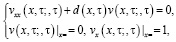
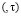 – произвольная точка области
– произвольная точка области 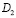 .
.
Интегрируя тождество (9) по области 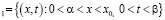 и пользуясь свойством функции Римана
и пользуясь свойством функции Римана 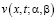 получим
получим
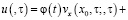
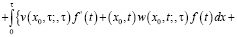
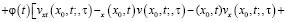
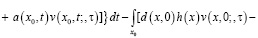
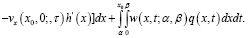 (13)
(13)
Формула (13) дает представление решения задачи Гурса (1), (10)-(12).
Тогда при выполнении условия 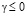 теоремы, выполняется неравенство
теоремы, выполняется неравенство
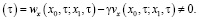
С учетом (14), используя условие склеивания (4), из соотношений (9) и (13) получаем интегральное уравнение Вольтерра второго рода относительно ϕ(τ)
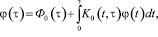 (15)
(15)
где
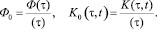
Так как с учетом гладкости известных функций
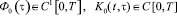 ,
,
то на основании свойств функций Римана 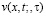 и
и 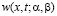 и условия теоремы, то единственное регулярное решение
и условия теоремы, то единственное регулярное решение 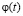 интегрального уравнения Вольтерра второго рода (15) из класса
интегрального уравнения Вольтерра второго рода (15) из класса 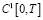 представимо в виде
представимо в виде
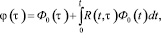 (16)
(16)
где 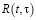 – резольвента ядра
– резольвента ядра 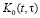 .
.
После определения функции 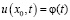 формулой (16) исследуемая задача распадается на две характеристические задачи (5) – (7) и (10) – (12) для псевдопараболического уравнения (1) единственные регулярные решения которых даются соответственно, формулами (9) и (13).
формулой (16) исследуемая задача распадается на две характеристические задачи (5) – (7) и (10) – (12) для псевдопараболического уравнения (1) единственные регулярные решения которых даются соответственно, формулами (9) и (13).
Из единственности регулярного решения указанных характеристических задач Гурса для уравнения (1) следует справедливость теоремы.
Нелокальные внутреннекраевые задачи для уравнений смешанного типа исследовались также в работах [3-7].



