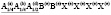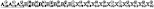Общая химическая формула шпинелей AB2X4. Структура шпинели имеет пространственную группу Fd3m и представляет собой плотнейшую кубическую трехслойную упаковку Х-атомов [1-4]. Элементарная ячейка шпинели состоит из 8 катионов А, которые занимают вайковые позиции 8(а), 16 катионов В, занимающих вайковые позиции 16(d), и 32 анионов Х, занимающих вайковые позиции 32(е). В этой статье мы рассмотрим возможные типы упорядочения атомов (возможные сверхструктуры) в тетраэдрических позициях 8(а) структуры шпинели.
Для нахождения всех возможных низкосимметричных фаз и соответствующих параметров порядка, базисных функций неприводимых представлений группы симметрии высокосимметричной фазы, а также расщепления правильных систем точек, занимаемых атомами в исходной кубической шпинели, нами использован теоретико-групповой метод, подробно описанный в [5-18].
Перестановочное представление на вайковой позиции 8(a) имеет размерность 16. Разложение этого представления на неприводимые преставления пространственной группы Fd3m следующее:
k 8(τ1) + k9(τ1+t4) +k10(τ3)+k11(τ1(A1g) + t4(A2u)) (1)
Обозначения волновых векторов и неприводимых представления даны по книге О.В. Ковалева [19]. Если рассмотреть приводимый параметр порядка (ПП) (1), то можно показать возможность существования 218 низкосимметричных упорядоченных фаз, включая фазу, индуцированную единичным представлением k11τ1(A1g). Как видно из таблицы среди этих фаз имеется 7 бинарных (фазы 1-6, 12) и 7 тройных (фазы 7-11, 14) сверхструктур. Упорядочение в бинарных сверхструктурах происходит по типам 1:1, 1:3, а тройных – по типам 1:1:2, 1:3:4. В таблице приведены также и вторичные (несобственные) ПП. Они помечены «sec».
Наиболее распространенными типами катионного упорядочения в позициях 8(а) являются структуры с пространственными группами 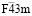 (параметр порядка (x), k11t4(A2u)) и
(параметр порядка (x), k11t4(A2u)) и 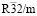 (параметр порядка (h, 0, 0, 0), k9(t4)).
(параметр порядка (h, 0, 0, 0), k9(t4)).
Структура упорядоченной шпинели с пространственной группой 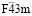 . Фазы с этой симметрией образуются в результате фазового перехода второго рода из кубической шпинели. Для многих шпинелей (MgAl2O4, LiGaCr4O8, CdJn2S4 и др.) фазовый переход действительно обнаружен экспериментально. Но есть и соединения, например LiXY4O8 (X= Ga, Fe, In; Y= Cr, Rh), которые вплоть до температуры плавления существуют в упорядоченной модификации. Для этих соединений исходная пространственная группа Fd3m является «прафазой».
. Фазы с этой симметрией образуются в результате фазового перехода второго рода из кубической шпинели. Для многих шпинелей (MgAl2O4, LiGaCr4O8, CdJn2S4 и др.) фазовый переход действительно обнаружен экспериментально. Но есть и соединения, например LiXY4O8 (X= Ga, Fe, In; Y= Cr, Rh), которые вплоть до температуры плавления существуют в упорядоченной модификации. Для этих соединений исходная пространственная группа Fd3m является «прафазой».
Критическое НП k11t4(A2u) входит в перестановочное представление шпинели на позициях 8(а) и 32(е) и в механическое представление на позициях 16(d) и 32(е). Образование структуры 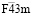 -фазы сопровождается упорядочением тетраэдрических катионов (порядок типа 1:1) и анионов (порядок типа 1:1), а также смещениями октаэдрических катионов и анионов. Расчетом установлено, что общая структурная формула упорядоченной шпинели есть A`4(a)A4(a)B16(e)4X416(e)X`416(e). Особенности строения
-фазы сопровождается упорядочением тетраэдрических катионов (порядок типа 1:1) и анионов (порядок типа 1:1), а также смещениями октаэдрических катионов и анионов. Расчетом установлено, что общая структурная формула упорядоченной шпинели есть A`4(a)A4(a)B16(e)4X416(e)X`416(e). Особенности строения 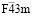 -фазы обсуждены в [7-9].
-фазы обсуждены в [7-9].
Порядок 1:1 в тетраэдрических узлах шпинели обнаружен в различных оксидных и сульфидных соединениях, а также в некоторых твердых растворах: λ-Li0.5Mn2O4, Li0.5CrxGa2.5-xO4 (x=1.75), Lil/2Fel/2[Cr2]O4, GaV4-xMoxS8 (0≤x£4), Cu1/2In1/2Cr2S4, Cu1/2Fe1/2Cr2S4, Ag1/2In1/2Cr2S4, LiXY4O8 (X=Ga, Fe, In; Y=Cr, Rh), CdIn2S4, MgAl2O4, Li0.5Fe1.0Rh1.5O4, FeIn2S4 и другие.
Структура упорядоченной шпинели с пространственной группой 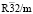 . Эта структура образуется в результате упорядочений и смещений тетраэдрических и октаэдрических катионов, а также анионов. Тетраэдрические катионы упорядочиваются по типу 1:1, октаэдрические катионы по типу – 1:1:6 и анионы по типу – 1:1:3:3. Структурная формула упорядоченной шпинели должна быть A2(c)1/2A`2(c)1/2B1(a)1/4B1(b)1/4B6(h)3/2X2(c)1/2X`2(c)1/2X6(h)3/2X`6(h)3/2. (для ромбоэдрической установки кристалла) и A6(c)1/2A`6(c)1/2B3(a)1/4B3(b)1/4B18(h)3/2X6(c)1/2X`6(c)1/2X18(h)3/2X`18(h)3/2. (для гексагональной установки кристалла). Структуру
. Эта структура образуется в результате упорядочений и смещений тетраэдрических и октаэдрических катионов, а также анионов. Тетраэдрические катионы упорядочиваются по типу 1:1, октаэдрические катионы по типу – 1:1:6 и анионы по типу – 1:1:3:3. Структурная формула упорядоченной шпинели должна быть A2(c)1/2A`2(c)1/2B1(a)1/4B1(b)1/4B6(h)3/2X2(c)1/2X`2(c)1/2X6(h)3/2X`6(h)3/2. (для ромбоэдрической установки кристалла) и A6(c)1/2A`6(c)1/2B3(a)1/4B3(b)1/4B18(h)3/2X6(c)1/2X`6(c)1/2X18(h)3/2X`18(h)3/2. (для гексагональной установки кристалла). Структуру 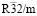 -фазы имеют AlV2O4, AlV2-xCrxO4 и Al1-xMgxV2O4, СuTi2S4, CuZr1.86S4.
-фазы имеют AlV2O4, AlV2-xCrxO4 и Al1-xMgxV2O4, СuTi2S4, CuZr1.86S4.
Бинарное и тройное катионное упорядочение в вайковой позиции 8(a) структуры шпинели 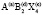
|
№ п/п |
Параметры порядка |
Символ пространственной группы |
V’/V |
Трансляции примитивной ячейки |
Стехиометрическая формула |
|
1 |
(0, 0, 0, j, j, 0)3 |
D43=P4122(N91) D47=P4322(N95) |
4 |
a1+a2+a3, 2a2, 2a3 |
|
|
2 |
(x)4 |
Td2= |
1 |
a1, a2, a3 |
|
|
3 |
(h, 0, 0, 0)4 |
D3d5= |
2 |
a1+a2, a1+a3, 2a1 |
|
|
4 |
(h, 0, 0, 0)1 |
D3d5= |
2 |
a1+a2, a1+a3, 2a1 |
|
|
5 |
(0, 0, 0, 0, j, j)3 |
D2h5=Pcmm(N51) |
2 |
a2+a3, a1, 2a2 |
|
|
6 |
(j, -j, -j, -j, -j, j)3 |
D3d5= |
4 |
a1+a2+a3, 2a2, 2a3 |
|
|
7 |
(0, j, 0, 0, 0, 0)3 (x)4sec. |
D2d5= |
2 |
a1+a2, a3, 2a1 |
|
|
8 |
(0, j, 0, j, 0, -j)3 (x)4sec. |
Td1= |
4 |
a1+a2+a3, 2a2, 2a1 |
|
|
9 |
(h, h, 0, 0)4 (0, 0, 0, 0, j, -j)3sec. |
D2h17=Bbmm(N63) |
4 |
a2+a3, 2a1, 2a2 |
|
|
10 |
(0, 0, h, h)1 (0, 0, 0, 0, j, j)3sec.\ |
D2h17=Ccmm(N63) |
4 |
a1, 2a2, 2a3 |
|
|
11 |
(ϕ1, -ϕ1, ϕ2, -ϕ2, ϕ2, ϕ2)3 |
C2h3=C2/m(N12) |
4 |
a1+a2+a3, 2a2, 2a3 |
|
|
12 |
(0, 0, q, q, 0, 0, 0, 0, q, q, 0, 0)1 |
C2h6=C2/c(N15) |
4 |
a1+a2-a3, 2a2, a1+a3 |
|
|
13 |
(0, 0, q, q, 0, 0, 0, 0, 0, 0, 0, 0)1 (x)4sec. |
D2d12= |
4 |
a1+a2-a3, 2a2, a1+a3 |
|
|
14 |
(0, 0, q, 0, 0, 0, 0, 0, 0, q, 0, 0)1 (0, 0, j, j, 0, 0)3sec. |
C2h3=C2/m(N12) |
4 |
a1+a2-a3, 2a2, a1+a3 |
|
Примечание. Обозначения для ПП: k8 – q, k9 – h; k10 – j, k11 – x. Верхний индекс после круглой скобки – номер представления по Ковалеву [19], V’/V – изменение объема примитивной ячейки в результате структурного фазового превращения. Верхний индекс в стехиометрической формуле – обозначение типа позиции по интернациональным таблицам.
Результаты работы получены при поддержке Минобрнауки РФ в рамках государственного задания на проведение НИОКР, шифр заявки N6.8604.2013.




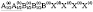
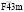 (N216)
(N216)
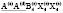
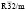 (N166)
(N166)
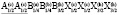
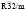 (N166)
(N166)
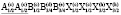
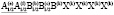
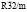 (N166)
(N166)
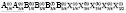
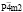 (N115)
(N115)
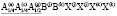
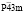 (N215)
(N215)
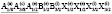
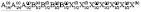
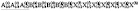
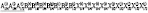
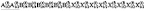
 (N122)
(N122)