Многие важные проблемы динамики плазмы, теории тепло- и массо – обмена в капиллярно-пористых средах, а также теории околозвуковых течений идеального газа и жидкости сводятся к локальным и нелокальным краевым задачам для гиперболического и смешанного типов уравнений, когда носителями граничных условий являются части характеристических кривых. Анализ литературы по гиперболическим уравнениям переноса влаги в пористых средах показал, что наиболее адекватными реальной ситуации моделями являются математические модели, в основе которых лежит уравнение А.В. Лыкова с младшим членом, учитывающим движение почвенной влаги под действием гравитационных сил
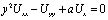 .
.
Это уравнение предложено А.В. Бицадзе [1] как пример уравнения, для которого при 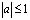 корректна по Адамару задача Коши, несмотря на нарушение известного условия Геллерстедта, а А.М. Нахушевым [5] как пример уравнения, для которого при
корректна по Адамару задача Коши, несмотря на нарушение известного условия Геллерстедта, а А.М. Нахушевым [5] как пример уравнения, для которого при 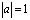 задача Дарбу не является корректной и характеристики не являются равноправными как носителя граничных данных. Вследствии прикладной важности возникла необходимость исследования нелокальных задач для уравнения А.В. Лыкова.
задача Дарбу не является корректной и характеристики не являются равноправными как носителя граничных данных. Вследствии прикладной важности возникла необходимость исследования нелокальных задач для уравнения А.В. Лыкова.
Цель: исследовать вопросы разрешимости нелокальной задачи с операторами дробного интегро-дифференцирования в краевом условии произвольного порядка и выяснить эффект влияния коэффициента при младшей производной на существование и единственность решения задачи.
Постановка задачи. Рассматривается уравнение влагопереноса Бицадзе – Лыкова
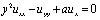 , (1)
, (1)
где a – действительная постоянная, причем 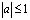 , в характеристическом треугольнике D, ограниченном характеристиками
, в характеристическом треугольнике D, ограниченном характеристиками
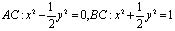
уравнения (1) и отрезком 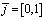 прямой
прямой 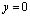 .
.
Задача. Найти регулярное в области D решение u(x,y) уравнения (1) из класса 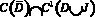 , удовлетворяющее краевым условиям
, удовлетворяющее краевым условиям
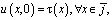 (2)
(2)
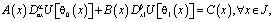 (3)
(3)
где 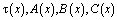 – заданные непрерывные функции, причем
– заданные непрерывные функции, причем 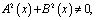
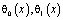 – точки пересечения характеристик уравнения (1), выходящих из точки
– точки пересечения характеристик уравнения (1), выходящих из точки 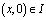 с характеристиками AC, BC соответственно; a, b – постоянные,
с характеристиками AC, BC соответственно; a, b – постоянные, 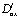 – операторы дробного в смысле Римана – Лиувилля интегро – дифференцирования, определяемые по формулам [12]
– операторы дробного в смысле Римана – Лиувилля интегро – дифференцирования, определяемые по формулам [12]
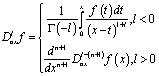
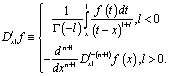
Задача (1)-(3) относится к классу краевых задач со смещением A.M. Нахушева [5]. Для обобщенного уравнения Трикоми задача (2)–(3) была исследована Оразовым И. [11] для различных интервалов изменения постоянных a, b. Нелокальные задачи со смещением для вырождающихся гиперболических и смешанного типов уравнений исследовались также в работах [2-5]–[7-11].
Доказательство существования решения задачи. Известно [1], что решение задачи Коши для уравнения (1) в области D при 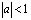 представимо в виде
представимо в виде
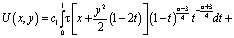
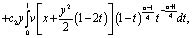 (4)
(4)
где 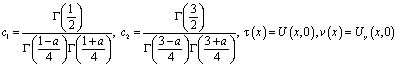 .
.
Удовлетворив (4) краевому условию (3), после преобразований получим уравнение
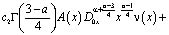
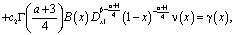 (5)
(5)
где
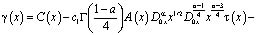
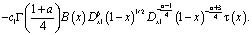
Теорема. Если
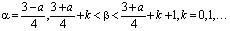 (6)
(6)
и выполнены условия
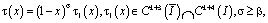 (7)
(7)
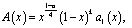
где 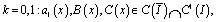 (8)
(8)
причем 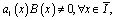
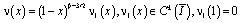 (9)
(9)
то задача (1)-(3) имеет более одного решения.
При выполнении условий (6) теоремы уравнение (5) примет вид
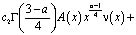
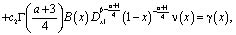 (10)
(10)
где
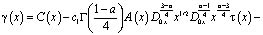
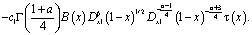
В случае, когда 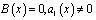 из (10) можно определить
из (10) можно определить
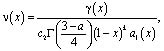
где k=0,1,…, т.е. решение задачи (1)-(3) существует и единственно.
Краткости ради исследуем вопрос разрешимости уравнения (10) при k=0 и k=1. С учетом свойств операторов дробного интегро-дифференцирования после соответствующих вычислений можно заключить, что правая часть g(x) уравнения (10) представима в виде
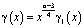 ,
,
где 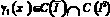 .
.
При выполнении условий (8) теоремы вопрос разрешимости задачи при k=0 эквивалентно редуцирован к вопросу разрешимости следующего интегро-дифференциального уравнения относительно n(x):
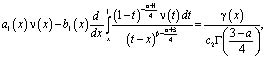 (11)
(11)
где 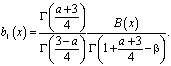
В этом случае справедливо неравенство 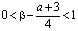 . Рассмотрим однородное уравнение, соответствующее (11)
. Рассмотрим однородное уравнение, соответствующее (11)
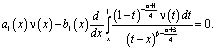 (12)
(12)
Введем новую неизвестную функцию
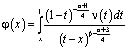 (13)
(13)
и, применяя формулу обращения
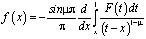
интегрального уравнения Абеля
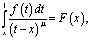
где 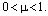 К (13), в результате получим уравнение
К (13), в результате получим уравнение
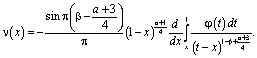
Подставляя последнее в (12) будем иметь
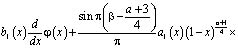
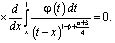 (14)
(14)
Если обозначить
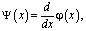 (15)
(15)
то с учетом равенства j(1)=С*, будем иметь
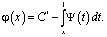 (16)
(16)
Подставляя (15), (16) в (14), получим при 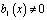 , что однородная задача (1)-(3), при k=0 эквивалентно в смысле разрешимости уравнению Вольтерра 2-го рода
, что однородная задача (1)-(3), при k=0 эквивалентно в смысле разрешимости уравнению Вольтерра 2-го рода
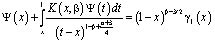 (17)
(17)
где 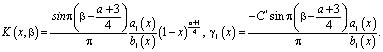
Методом последовательных приближений можно показать, что уравнение (17) имеет нетривиальное решение в классе функций
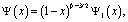
где 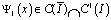 .
.
Таким образом, при k=0 решение задачи (1)-(3) неединственно.
Докажем теперь существование решения задачи (1)-(3) в случае k=0. Уравнение (11) в результате введения функции j(x), а затем и Y(x) по формулам (13), (15) принимает вид
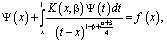 (18)
(18)
где
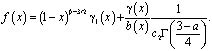
С учетом гладкости известных функций правая часть уравнения (18) представима в виде
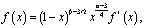
где 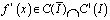 .
.
В этом классе функций уравнение (18) имеет нетривиальное решение Y(x). По найденному Y(x) определяется j(x), а затем n(x). Таким образом, задача разрешима и ее решение задается формулой (4).
Исследуем теперь вопрос разрешимости задачи (1)-(3) при k=1. В этом случае выполняется неравенство 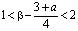 . И уравнение (10) при выполнении условий теоремы имеет вид
. И уравнение (10) при выполнении условий теоремы имеет вид
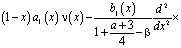
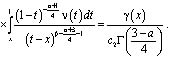 (19)
(19)
Покажем, что однородное уравнение, соответствующее (19), имеет нетривиальное решение. В самом деле, рассмотрим уравнение
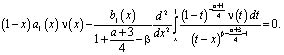 (20)
(20)
Вычислениями, аналогичными случаю k=0 уравнение (20) преобразуется к виду:
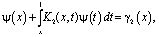 (21)
(21)
где
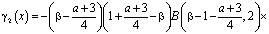
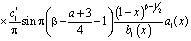
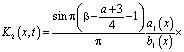
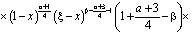
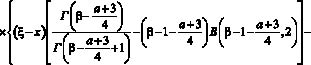
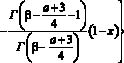 .
.
Уравнение (21) есть интегральное уравнение Вольтера второго рода с непрерывной правой частью 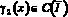 и непрерывным ядром
и непрерывным ядром 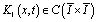 и, следовательно, оно имеет единственное непрерывное на
и, следовательно, оно имеет единственное непрерывное на 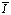 решение
решение 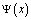 , определяемое формулой
, определяемое формулой
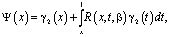
где R(x,t,b) – резольвента ядра 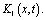 Таким образом, неединственность решения задачи при k=1 доказана.
Таким образом, неединственность решения задачи при k=1 доказана.
Установим существование решения задачи при k=1. С учетом ранее введенных обозначений и проведенных преобразований уравнение (19) примет вид
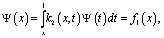 (22)
(22)
где
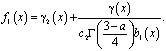
На основании ранее приведенных исследований заключаем, что правая часть (22) представима в виде
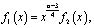
где 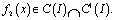 В этом классе функции уравнение (22) имеет нетривиальное решение Y(x). По найденному Y(x) можно определить n(x). Следовательно, при k=1 задача (1)-(3) разрешима и ее решение задается формулой (4)
В этом классе функции уравнение (22) имеет нетривиальное решение Y(x). По найденному Y(x) можно определить n(x). Следовательно, при k=1 задача (1)-(3) разрешима и ее решение задается формулой (4)
По найденному n(x) решение u(x,y) задачи (1) – (3) в области D определяется по формуле (4).



