Теория краевых задач для уравнений смешанного типа, в силу теоретической и прикладной важности, является одним из интенсивно развивающихся разделов современной теории дифференциальных уравнений с частными производными. Многие математические модели тепло- и массообмена в средах, окруженных пористой средой, сводятся к краевым задачам для уравнений смешанного типа. Смешанные гиперболо–параболические уравнения лежат в основе математических моделей различных природных явлений. Локальные и нелокальные краевые задачи для таких уравнений встречаются в теории распространения электромагнитных полей, при изучении математических моделей, описывающих влияние растительного покрова на теплообменные процессы в почве и приземном воздухе, при котором возникает необходимость исследования задачи для двух уравнений
Цель исследования: доказать однозначную разрешимость внутреннекраевой задачи с операторами дробного дифференцирования для уравнения смешанного типа второго порядка.
Постановка задачи. Рассматривается уравнение
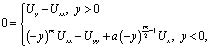(1)
где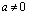 
– вещественная постоянная, 
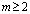, в конечной области W, ограниченной отрезками AA0, BB0, A0B0 прямых x=1, x=1, y=1 соответственно, лежащих в полуплоскости y>0, и характеристиками
,
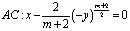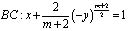
уравнения (1) в полуплоскости y<0. Пусть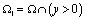 
, 
, 
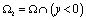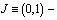интервал прямой y=0.
Задача. Найти регулярное в области W при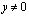 
решение U(x,y) уравнения (1), непрерывное в 
и удовлетворяющее условиям
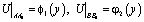, (2)
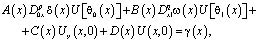(3)
где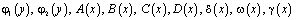 
– заданные непрерывные функции, причем 
, 
, 
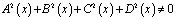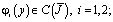
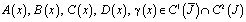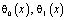– точки пересечения характеристик уравнения (1), выходящих из точки (x,0), с характеристиками AC, DC соответственно, 
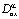– операторы дробного в смысле Римана – Лиувилля интегро-дифференцирования [11].
Единственность решения задачи. При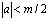 
решение задачи Коши
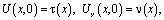в области Ω2 имеет вид [1, 10]
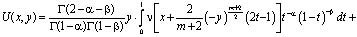
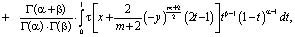(4)
где Г(a) – гамма функция Эйлера [3].
Вычислим
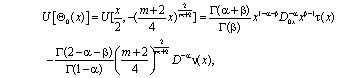
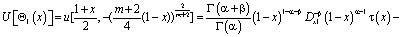
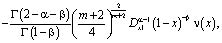
где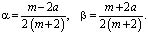 
Пусть
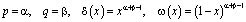. (5)
Подставив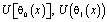 
в (3), после преобразований получим соотношение между t(x) и n(x), принесенное из Ω2 на J
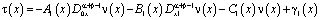, (6)
где 
,
,
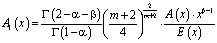
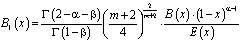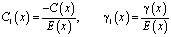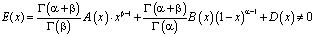. (7)
Если выполняются условия
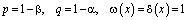, (8)
то функциональное соотношение из гиперболической части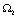 
на J имеет вид
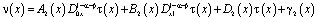, (9)
где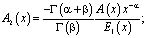 
,
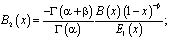
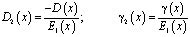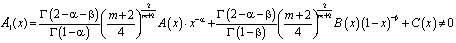. (10)
Теорема единственности. В области W не может существовать более одного решения задачи (1) – (3), если выполняется либо (5) и (7),
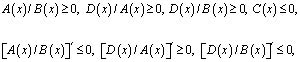(11)
либо (8) и (10),
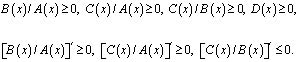(12)
Докажем, что при выполнении условий (5), (7), (11) теоремы решение задачи единственно. Для этого докажем, что интеграл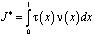 
не может быть отрицательным.
В самом деле, при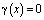 
уравнение (6) примет вид
.
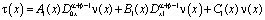Отсюда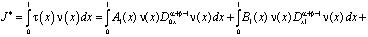 
.
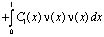Используя методику, применявшуюся в работах [2, 5-9] получим следующее равенство
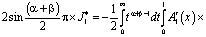
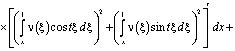
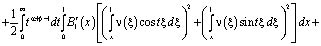
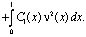
Таким образом, при выполнении условий (5), (7), (11) теоремы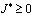 
.
С другой стороны, переходя в уравнении (1) к пределу при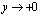 
, получаем
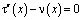. (13)
Из (13) имеем
.
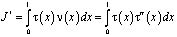Интегрируя по частям при выполнении однородных граничных условий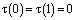 
, будем иметь
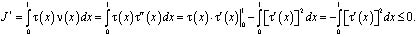
Отсюда заключаем, что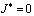 
. И, следовательно,
, 
.
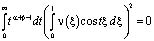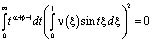Так как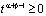 
, то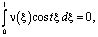 
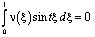
для всех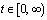 
, в частности, при 
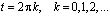. При этих значениях t функции sintx и costx образуют полную ортогональную систему функций в L2. Следовательно, 
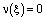почти всюду, а так как n(x) непрерывна по условию, то 
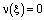всюду. Отсюда легко видеть, что 
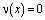и из (6) при 
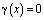следует, что 
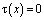. Следовательно, 
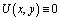в Ω2 как решение задачи Коши с нулевыми данными, а в Ω1 U(x,y)=0 как решение первой краевой задачи с нулевыми данными.
Таким образом, при выполнении условий (5), (7), (11) теоремы решение задачи единственно. При выполнении условий (8), (10), (12) теоремы единственность решения задачи доказывается анало гично.
Существование решения задачи. При выполнении условий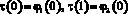 
интегрируя дважды (13) из Ω1 получим
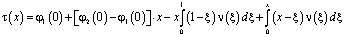. (14)
Пусть выполняются условия (5). Исключая t(x) из (14) и (6) вопрос разрешимости задачи (1) – (3) эквивалентно редуцируется к вопросу разрешимости интегрального уравнения
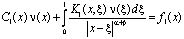, (15)
где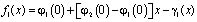 
,
.
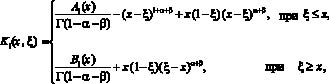
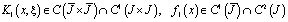При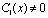 
уравнение (15) есть интегральное уравнение Фредгольма второго рода, однозначная и безусловная разрешимость которого заключается из единственности решения задачи. По найденному n(x) определяется t(x) из (6). Решение задачи (1) – (3) в области Ω2 выписывается как решение задачи Коши, а в области Ω1 как решение первой краевой задачи [4]. При выполнения условий (8) теоремы существование решения задачи устанавливается также путем редукции к уравнению Фредгольма второго рода.