Scientific journal

Advances in current natural sciences

ISSN 1681-7494

"Перечень" ВАК

ИФ РИНЦ = 0,775

Нахождение стехиометрических коэффициентов в уравнениях химических реакций – одна из распространенных задач химии. Так называемый подбор коэффициентов является весьма часто употребляемым способом [1]. Однако при рассмотрении реакций с многоатомными молекулами, ионами, элементами различных степеней окисления подобный подход может оказаться неэффективным и приводить к ошибочным результатам.

Принято считать, что первое изложение метода определения коэффициентов в химических уравнениях было дано в 1878 г. [8] на основании закона сохранения массы, сформулированного Лавуазье.

В учебниках по общей химии и в ряде статей Journal of Chemical Education приводятся различные примеры применения алгебраического метода нахождения стехиометрических коэффициентов [2, 6, 8]. Он формализует следующую задачу: имеются вещества B1, …Bn и требуется составить химическую реакцию между ними в виде уравнения с целочисленными коэффициентами

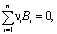(1)

где ni – молярный стехиометрический коэффициент, отрицательный – для реагентов (т.к. они расходуются), положительный – для продуктов реакции (накапливаются) и равный нулю для веществ, не участвующих в реакции. Для стехиометрии подобное разделение носит несколько условный характер: важно, чтобы коэффициенты реагентов и продуктов имели противоположные знаки. Для решения этой задачи формула каждого из веществ Bi представляется через совокупности некоторых структурных единиц (СЕ) E1, …Em , в качестве которых могут быть атомы, ионы, оксиды, радикалы и т.п., в виде соотношения:

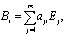(2)

где aji – коэффициенты СЕ в химической формуле вещества Bi. После подстановки соотношений (2) в уравнение (1) и изменения порядка суммирования, можно записать систему из m однородных линейных уравнений относительно n стехиометрических коэффициентов в виде:

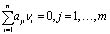(3)

Эту систему часто представляют в матричной форме [2, 9]. Действительно, левая часть (3), очевидно, равна произведению двух матриц A·q, причем q – одностолбцовая матрица из n стехиометрических коэффициентов, a (m, n) – матрица А, элементами которой являются коэффициенты aji, может быть как прямоугольной (m ¹ n), так и квадратной (m = n). В последнем случае целочисленные решения системы (3) могут оказаться в одном или нескольких столбцах так называемой присоединенной матрицы, обычно обозначаемой adj(А) или adjoint(А), с элементами в виде алгебраических дополнений вместо соответствующих элементов матрицы А [4]. (Отметим, что матрица adj(А) равна произведению определителя матрицы А на обратную к ней.)

Если m¹ n, т.е., матрица – прямоугольная, то для нахождения стехиометрических коэффициентов в ряде случаев можно использовать так называемую ступенчатую форму матрицы А. Она, как известно, может быть получена при многократном использовании метода исключения Гаусса для решения системы (3) и часто обозначается rref(А). В этой матрице обычно последний столбец образован отношениями стехиометрических коэффициентов: i/n, i = 1,…,(n –1).

В общем случае, когда n – m = r ³ 1, а элементы матрицы А – целочисленные, уравнения (3) можно рассматривать как систему однородных линейных диофантовых уравнений (СДУ), решения которой будут содержать r произвольных постоянных. Добавление дополнительных ограничений на стехиометрические коэффициенты приводит к уменьшению числа r и, когда оно достигает значения 1, оказывается, что произвольная постоянная присутствует в каждом из коэффициентов в виде множителя, после сокращения на который и получается их единственный набор.

Вычисления, выполняемые «вручную», часто достаточно трудоемки и естественно желание исследователя использовать такие вычислительные средства, в которых наиболее громоздкие этапы расчетов выполнялись бы автоматически. В качестве подобного средства может быть рекомендована система компьютерной алгебры Maple, различные версии которой достаточно подробно описаны в ряде пособий и руководств (например, [3]). Она особенно эффективна в тех случаях, когда некоторые (или все) коэффициенты матрицы A содержат символы с интервалом значений (так, например, в химической петрологии в уравнении реакции взаимодействия граната пироп-альмандинового ряда с кордиеритами формула одного из последних записывается в виде (Fe0.5+k,Mg1.5-k)Al4Si5O18 и содержит переменный параметр 0 < k < 1.5, характеризующий «железистость» при изоморфном замещении Fe и Mg). В литературе применение Maple для вычисления стехиометрических коэффициентов обсуждалось, однако ряд вопросов остался не рассмотренным [10].

Настоящая работа посвящена таким ранее не обсуждавшимся возможностям системы Maple как отсутствие или множественность решений СДУ, способы учета дополнительных ограничений для выявления единственного набора коэффициентов. Последний вопрос был частично рассмотрен в [5].

Проиллюстрируем применение Maple следующей простой реакцией разложения тринитротолуола, C7H5N3O6 на такие продукты как N2, CO и H2O. В качестве СE возьмем элементы: C, H, N, O.

В системе Maple каждая команда или несколько команд записываются после приглашения > и заканчивается знаком : (результат не высвечивается) или знаком ; (результат высвечивается), после символа # обычно следует комментарий, символ % (так называемый ditto – оператор) означает обращение к предыдущему результату.

Ниже приведена распечатка (с комментариями) этой задачи в виде примеров 1 и 2 в среде Maple.

> #Пример 1.

> restart:#начало работы или новой задачи

> #нумерация реагентов: C7H5N3O6-1, N2-2, CO-3, H2O-4

> C:=[7,0,1,0]:H:=[5,0,0,2]:N:=[3,2,0,0]:O:=[6,0,1,1]:#списки СЕ

> А:=matrix([C,H,N,O]):#построение квадратной матрицы из списков СЕ

> with(linalg):#подключение библиотеки линейной алгебры для выполнения матричных операций

> adjoint(А):map(x->-x,col(%,2)),map(x->x/2,col(%,4));#вычисление присоединенной матрицы и выделение из нее второго и четвертого столбцов, содержащих значения стехиометрических коэффициентов в выбранном ранее порядке нумерации реагентов.

[-2 3 14 5], [-2 3 14 -2]

> #2C7H5N3O6 = 3N2 +14CO +5 H2O #нет баланса по кислороду

> #2C7H5N3O6 + 2H2O = 3N2 + 14CO #нет баланса по водороду и лишний реагент в левой части

> a:=matrix([[nu[1]],[nu[2]],[nu[3]],[nu[4]]]):#матрица из стехиометрических коэффициентов

> Q:=multiply(А,a):#левые части системы четырех уравнений типа (3)

> isolve({Q[1,1],Q[2,1],Q[3,1]});#целочисленное решение системы первых трех уравнений

{ν1=2_Z1, ν2=–3_Z1, ν3=–14_Z1, n4=–5_Z1}

Как видно из результатов, коэффициенты в столбцах присоединенной матрицы не отвечают выполнению баланса по кислороду или по водороду, что следует и из решения СДУ. Это значит, что химическую реакцию между реагентами уравнять не возможно, так как, вероятно, не учитывается еще какой-то продукт реакции. Пусть им будет C – углерод. Тогда, повторяя команды примера 1 с учетом C в качестве еще одного продукта, получим следующий результат:

> #Пример 2.

> restart:

> C:=[7,0,1,0,1]:H:=[5,0,0,2,0]:N:=[3,2,0,0,0]:Ox:=[6,0,1,1,0]:

> A:=matrix([C,H,N,Ox]):#прямоугольная матрица

> rref(A):map(x->-x,col(%,5));#вычисление ступенчатой матрицы; после выделения из нее пятого столбца и умножения всех его элементов на -1 получаем отношения первых четырех коэффициентов к пятому

<<marin6.wmf>>

> #после приведения к общему знаменателю получаем:

-2C7H5N3O6 + 3N2 + 7CO + 5H2O + 7C = 0;

> a:=matrix([[nu[1]],[nu[2]],[nu[3]],[nu[4]],[nu[5]]]):

> Q:=multiply(A,a):

> S:=isolve({Q[1,1],Q[2,1],Q[3,1],Q[4,1]}); #общее решение СДУ

S:={}

> subs(_Z1=-1,S); #частное решение СДУ

{ν1=–2, ν2=3, ν3=7, n4=5, n5=7}

> #окончательный результат: 2C7H5N3O6 = 3N2 + 7CO + 5H2O + 7C

Из примера 2 следует, что в общем решении СДУ, представленном массивом S, все коэффициенты включают произвольный параметр _Z1 в виде множителя. После сокращения на него получаем единственный набор, в котором отношения первых четырех коэффициентов к пятому полностью согласуются с результатами расчета ступенчатой матрицы.

В табл. 1 приведены некоторые совокупности реагентов и продуктов, для которых подобно вышеприведенному примеру 2 стехиометрические коэффициенты в уравнениях реакции содержат только один произвольный параметр _Z1. В строках 1 – 9 табл. 1 числа m и n различаются на единицу. В строке 10 реагенты приведены в ионной форме и, так как значения m и n оказываются равными 4 и 6 соответственно, для увеличения числа уравнений на единицу добавляется условие электронейтральности (УЭН), которое здесь может быть представлено списком [3, -1, 2, 5, 0], похожим на список для СЕ. В строке 11 табл. 1 значения m и n различаются на 3, поэтому к УЭН добавляется еще и «баланс» по кислороду (O2), что может быть записано следующим образом: [0,-1,1,0,2,0] и [1,0,0,1,0,0]. Таким образом, все рассмотренные в таблице примеры оказываются «однопараметровыми».

Таблица 1

Однопараметровые (_Z1) уравнения химических реакций

Однако, если общее решение СДУ содержит произвольных параметров более, чем один, то для получения частного решения может потребоваться дополнительная информация. Покажем это на реакции окисления этилбензола (C6H5C2H5) перманганатом калия (KMnO4) в кислой среде (H2SO4) с образованием следующих продуктов: C6H5COOH, K2SO4, MnSO4, CO2 и H2O [5]. В качестве СЕ будем, как и ранее, использовать элементы C, H, K, Mn, O и S.

> #Пример 3.

> restart:

> #нумерация реагентов: C6H5C2H5 – 1, KMnO4 – 2, H2SO4 – 3, C6H5COOH – 4,

K2SO4 – 5, MnSO4 – 6, CO2 – 7, H2O – 8

> C:=[8,0,0,7,0,0,1,0]:H:=[10,0,2,6,0,0,0,2]:K:=[0,1,0,0,2,0,0,0]:

Mn:=[0,1,0,0,0,1,0,0]:O:=[0,4,4,2,4,4,2,1]: S:=[0,0,1,0,1,1,0,0]:

> A:=matrix([C,H,K,Mn,O,S]):

> with(linalg):

> a:=matrix([[nu[1]],[nu[2]],[nu[3]],[nu[4]],[nu[5]],

[nu[6]],[nu[7]],[nu[8]]]):

> Q:=multiply(A,a):

> S:=isolve({Q[1,1],Q[2,1],Q[3,1],Q[4,1],Q[5,1],Q[6,1]}); #общее решение СДУ

S:={ν1=5_Z1, ν2=42_Z1+6Z2, ν3=63_Z1+9_Z2, n4=_Z2, n5=–21_Z1–3_Z2, n6=–42_Z1–6_Z2, n7=–40_Z1–7_Z2, n8=–88_Z1–12_Z2}

> subs(_Z1=-1,_Z2=5,S);#частное решение СДУ

ν1=–5, ν2=–12, ν3=–18, n4=5, n5=6, n6=12, n7=5, n8=28

В общем решении примера 3 имеются два произвольных параметра _Z1 и _Z2. Для получения частного решения принято во внимание то обстоятельство, что только этилбензол и бензойная кислота содержат фрагмент C6H5, вследствие чего их коэффициенты должны различаться только знаком. Поэтому, если положить _Z1=-1 и_Z2=5, то уравнение реакции принимает следующий вид:

5 C6H5C2H5 + 12 KMnO4 + 18 H2SO4 = 5 C6H5COOH + 6 K2SO4 + 12 MnSO4 + + 5 CO2 + 28 H2O

Можно «наличие» ароматической группы задать списком phenyl:=[1,0,0,1,0,0,0,0] и поместить его в матрицу A среди списков для СЕ, тогда после проведения аналогичных операций общеe решениe СДУ будет содержать только один произвольный множитель:

{ν1=–5_Z1, ν2=–12_Z1, ν3=–18_Z1, n4=5_Z2, n5=6_Z1, n6=12_Z1, n7=5_Z1, n8=28_Z1}

Заметим также, один из столбцов ступенчатой формы «расширенной» подобным образом матрицы A (rref(A)) содержит отношения первых семи коэффициентов к восьмому в следующем виде:

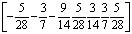
Это подтверждает правильность найденных коэффициентов.

Иногда выявление дополнительных ограничений для получения единственного набора коэффициентов достаточно сложная задача. Покажем это на примере гидролиза брадикинина (C50H73N15O11) – Br [6], продуктами которого являются аминокислоты глицин (C2H5NO2) – Gly, серин (C3H7NO2) – Ser, аргинин (C6H14N4O2) – Arg, пролин (C5H9NO2) – Pro и фенилаланин (C9H11NO2) – Phe. В качестве СЕ будем, как и ранее, использовать элементы: C, H, N, O.

> #Пример 4.

> restart:

> #нумерация реагентов: Br-1,W-2,Gly-3,Ser-4,Arg-5,Pro-6,Phe-7

> C:=[50,0,2,3,6,5,9]:H:=[73,2,5,7,14,9,11]:

N:=[15,0,1,1,4,1,1]:Ox:=[11,1,2,3,2,2,2]:

> A:=matrix([C,H,N,Ox]):#матрица прямоугольная

> q:=matrix([[nu[1]],[nu[2]],[nu[3]],[nu[4]],

[nu[5]],[nu[6]],[nu[7]]]):

> with(linalg):

> Q:=multiply(A,q):

> S:=isolve({Q[1,1],Q[2,1],Q[3,1],Q[4,1]):

{ν1 =_Z1, ν2 =12_Z1+2_Z2+5_Z3, ν3 =-13_Z1-6_Z2+6_Z3, n4 =7_Z1+

+4_Z2-5_Z3, n5 =_Z2, n6 =-9_Z1-3_Z2-3_Z3, n7 =_Z2+2_Z3}

> subs(_Z1=-1,_Z2=2,_Z3=0,S): subs(_Z1=-2,_Z2=3,_Z3=-1,S)

:subs(_Z1=-4,_Z2=5,_Z3=-2,S):#три набора решений I, II, III:

Таблица 2

Наборы стехиометрических коэффициентов (I, II, III) реакции гидролиза брадикинина

Таким образом, для гидролиза брадикинина при выборе в качестве СЕ атомов C, H, N и O формально получено три набора стехиометрических коэффициентов. Дополнительным критерием в данном случае является их четность (вариант II) или их кратность четырем (вариант III). Действительно, при гидролизе четырех эквивалентных молекул брадикинина (ν1 = 4) образование 27 молекул пролина (n6 = 27) следует признать невозможным, равно как и трех молекул аргинина (n5=3) или одной молекулы фенилаланина (n7 = 1). По этой причине набор коэффициентов (III) должен быть исключен из рассмотрения. Аналогично, при гидролизе двух молекул брадикинина (ν1 = 2) образование продуктов с нечетными коэффициентами n5,n6 и n7 также невозможно, так что вариант (II) также должен быть исключен. Следовательно, остается единственный ответ (I), который соответствует следующему уравнению:

C50H73N15O11 + 8*H2O = C2H5NO2 + +C3H7NO3 + 2*C6H14N4O2 + +3*C5H9NO2 +2*C9H11NO2.

Этот же набор коэффициентов как единственный был установлен в работе [6].

В заключение отметим, что рассмотренные выше способы нахождения коэффициентов в среде Maple, основанные на использовании элементов в качестве СЕ, вполне универсальны, а учет дополнительных ограничений на основе особенностей сочетания структуры реагентов и продуктов позволяет получить число уравнений, отличающееся от числа переменных на единицу, и, как следствие, единственный набор коэффициентов в уравнении реакции.