Scientific journal

Advances in current natural sciences

ISSN 1681-7494

"Перечень" ВАК

ИФ РИНЦ = 0,775

Для композиционных покрытий на основе системы никель-фосфор-фторопласт [1-13] и электролитических покрытий на основе системы никель-бор-фторопласт [14-21] зарегистрирован эффект синергизма проявления износостойких и антифрикционных свойств. Установлено, что синергизм твердой и смазочной компонент композиционных покрытий заключается в концентрировании фаз смазочной компоненты на поверхности трения и в наличии наночастиц твердых фаз (Ni3Р, Ni2Р, Ni [4, 5, 12] или Ni3B, Ni2B, Ni [14-16]), проявляющих свойства твердых смазок. В работах [1, 12, 22] показано, что износостойкость покрытий при трибологическом воздействии может быть обусловлена, в частности, способностью твердых фаз, в том числе и фазы Ni (Fm3m), к самовосстановлению за счет обратимых фазовых превращений.

Возможные фазовые превращения в кристаллах с Fm3m симметрией без изменения ячейки могут быть получены на основе сравнения результатов теоретико-группового анализа высокосимметричных точек G и C в ГЦК зоне Бриллюэна [23] и результатов теоретико-решеточного анализа вероятных фаз с занятыми F-подрешеткой или подрешетками, образующимися при ее расслоении [24]. В табл. 1 для каждого варианта расслоения исходного кубического решеточного комплекса приведены возможные полиморфные модификации «материнской» Fm3m-фазы. Первая строка табл. 1 представлена изорешеточными низко симметричными модификациями, в которых атомами заняты одинаковые подрешетки. Эти модификации отличаются между собой наборами остальных подрешеток и их характеристиками (кратностью, локальной симметрией).

Таблица 1

Симметрия фаз, образующихся при обратимых фазовых превращениях второго рода из Fm3m-фазы с занятым решеточным комплексом F

Среди приведенных в таблице 1 фаз присутствуют и деформационные модификации.

В случае совпадения вектора деформации ячейки с осью третьего порядка Fm3m-фазы имеем вариант плотнейшей гексагональной упаковки тригональных слоев из атомов никеля и возможное при трении образование наночастиц. Цепочки обратимых фазовых превращений второго рода, сохраняющих ось третьего порядка Fm3m-фазы в кубических и ромбоэдрических модификациях фаз, могут быть следующими:

Fm3m ↔ (Pm3m, Pn3m, P4232) ↔ (Pm3, Pn3, Pa3);

Fm3m ↔ R3m ↔ (R3, R3m, R32) ↔ R3;

Fm3m ↔ (F`43m, F432) ↔ (R3m, R32) ↔ R3.

В случае совпадения вектора деформации ячейки с осью четвертого порядка Fm3m-фазы имеем вариант плотной тетрагональной упаковки квадратных слоев из атомов никеля. Цепочки обратимых фазовых превращений второго рода, сохраняющих ось четвертого порядка Fm3m-фазы в кубических и тетрагональных, модификациях фаз, могут быть следующими:

Fm3m ↔ (F`43m, Fm3, F432) ↔ (P4/mmm, P422, P4/m);

Fm3m ↔ P4232 ↔ (Pn3m, Pn3) ↔ (I4/mmm, I422, I4/m);

Fm3m ↔ (P42/ncm) ↔ (P4/mcc, P4cc).

Если вектор деформации ячейки с осью второго порядка Fm3m-фазы, то цепочки обратимых фазовых превращений второго рода, сохраняющих эту ось Fm3m-фазы в кубических, ромбических и моноклинных модификациях фаз, могут быть следующими:

Fm3m ↔ (Pm3m, Pn3m, P4232) ↔ (P222, P2/m);

Fm3m ↔ F432 ↔ (Pnnm, Immm) ↔ I222;

Fm3m ↔ (F`43m, F432) ↔ (Pccn, Pccm) ↔ Pmma.

На основе анализа фазово-разупорядоченного состояния трибосопряженных поверхностей в соответствии с методиками [25-34] и учета вероятного эффекта синергизма свойств компонентов покрытий за счет размерного и наноструктурного факторов возможен целенаправленный выбор эффективных модификаторов [1, 7-12]. Проанализируем некоторые из вероятных наноструктур с атомными оболочками фуллеренов октаэдрической ветви классификации. Характеристики всех полиэдров с симметрией октаэдра Oh, представлены в табл. 2.

Таблица 2

Характеристика полиэдров с симметрией Oh

Топологические преобразования с сохранением симметрии октаэдра Oh определяются известными соотношениями:

O{3333} → tO{466} → CO{3434} → tC{388} → C{444},

CO{3434} → tCO{468}→ RCO{3444},

tO{466} → {2{3.8.12}+{3.12.12}} → {3436}.

Данные о возможных деформационных полиморфных модификациях для полиэдров с кубической симметрией могут быть получены при анализе фундаментальной области точечной группы Оh. Симметрический комплекс группы содержит центр симметрии, 12 поворотных осей симметрии 2-го порядка, 4 инверсионные оси симметрии 3-го порядка, 6 поворотных осей симметрии 4-го порядка и 12 плоскостей симметрии m. Фундаментальная область группы – замкнутая неправильная трехгранная пирамида, ребрами которой являются ближайшие друг к другу оси симметрии 2-го, 3-го и 4-го порядка (рис. 1). Используемые в табл. 3 структурные элементы фундаментальной области точечной группы Oh для фуллереноподобных наночастиц в форме усеченного октаэдра и в форме усеченного куба указаны на рис.1,б и 1,г, соответственно.

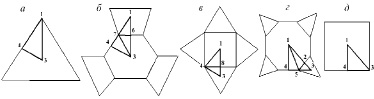
Соотношения структурных элементов модификаций фуллереноподобных частиц с симметрией Oh: O{3333} (а), tO{366} (б), СO{3434} (в), tC{388} (г), C{444} (д)

Таблица 3

Возможные структурные состояния фуллереноподобных наночастиц в форме усеченного октаэдра или усеченного куба

Таким образом, установлено, что фазовая и структурная разупорядоченность на поверхности композиционных покрытий после трибовоздействия может быть обусловлена, в частности, наличием фуллереноподобных наночастиц никеля с диаметром менее 0,5 нм с симметрией группы Oh и их вероятных деформационных модификаций. Все подобные наночастицы в соответствии с синергической моделью могут рассматриваться как «фазы» твердой компоненты, проявляющие свойства твердых смазочных материалов и эффективно влияющие на трибологические свойства покрытий [1, 12].

Отметим, что для уточнения величины эффекта синергизма квазифрактальный характер структурной организации поверхности композиционных покрытий также может быть учтен по предлагаемым в [35-46] методикам формирования, описания и интерпретации вероятных поверхностных фрактальных структур. Показано, что в случае трибологических воздействий квазифрактальные структуры могут быть аппроксимированы детерминистическими модулярными фракталами в 2D пространстве [47-52].