В пространстве C3 комплексных переменных x,y,z рассмотрим уравнение

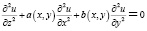, (1)

где a(x,y) и b(x,y) – аналитические функции, принимающие вещественные значения при вещественных значениях независимых переменных x,y, и при вещественных значениях x,y,z уравнение эллиптично. Пусть коэффициенты a(x,y) и b(x,y) аналитичны в некоторой области голоморфности B из пространства C2 независимых комплексных переменных x,y.

Для уравнения (1) рассмотрим задачу Коши в следующей постановке: найти голоморфное решение u уравнения (1), удовлетворяющее начальным условиям

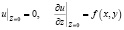, (2)

где функция f(x,y) голоморфна в круговом бицилиндре 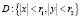, лежащем в B.

Для решения этой задачи получено следующее представление

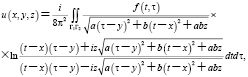
где интегрирование совершается по остову 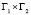границы бицилиндра D.