В настоящее время теория краевых задач для уравнений смешанного типа является одним из интенсивно развивающихся разделов современной теории дифференциальных уравнений с частными производными. Одним из важнейших классов уравнений с частными производными являются нагруженные уравнения смешанного типа. Подробная библиография по исследованиям локальных и нелокальных краевых задач для нагруженных уравнений содержится в [10].
Цель исследования: доказать существование и единственность решения нелокальной задачи для нагруженного уравнения третьего порядка с кратными характеристиками.
Постановка задачи
В области
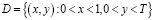
рассматривается нагруженное уравнение третьего порядка с кратными характеристиками
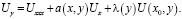 (1)
(1)
Задача. Найти регулярное в области D решение 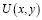 уравнения (1) из класса
уравнения (1) из класса 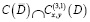 с непрерывной вплоть до
с непрерывной вплоть до 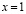 производной первого порядка по x, удовлетворяющее условиям:
производной первого порядка по x, удовлетворяющее условиям:
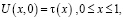 (2)
(2)
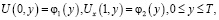 (3)
(3)
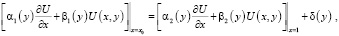
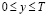 , (4)
, (4)
где 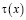 ,
, 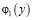 ,
, 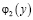 ,
, 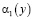 ,
, 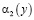 ,
, 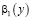 ,
, 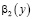 ,
, 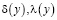 – заданные функции, непрерывные в замыкании области их определения;
– заданные функции, непрерывные в замыкании области их определения; 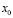 – фиксированная точка интервала
– фиксированная точка интервала 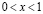 , причем
, причем 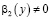 .
.
Рассмотрим сначала случай, когда 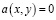 , тогда уравнение (1) примет вид
, тогда уравнение (1) примет вид
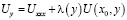 . (5)
. (5)
Пусть существует решение 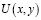 задачи (1) – (4) и
задачи (1) – (4) и
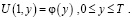 (6)
(6)
Из свойств функции Грина 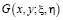 [6] заключаем, что решение
[6] заключаем, что решение 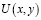 задачи (1) – (3), (6) в области D представимо в виде
задачи (1) – (3), (6) в области D представимо в виде
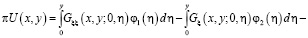
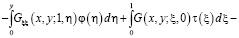
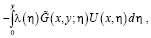 (7)
(7)
где 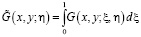 .
.
Обозначая 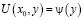 , получаем из (7) интегральное уравнение Вольтерра второго рода
, получаем из (7) интегральное уравнение Вольтерра второго рода
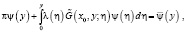 (8)
(8)
которое однозначно разрешимо в классе непрерывных функций, где 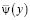 – известная, достаточно гладкая функция.
– известная, достаточно гладкая функция.
Таким образом, решение задачи (1) – (3) при выполнении условия (7) имеет вид
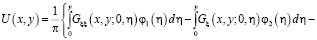
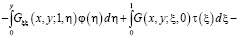
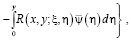 (9)
(9)
где 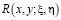 – резольвента ядра
– резольвента ядра 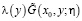 .
.
Дифференцируя (9) по x, и подставляя 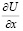 в краевое условие (4), после несложных преобразований получим интегральное уравнение Вольтерра второго рода относительно неизвестной функции
в краевое условие (4), после несложных преобразований получим интегральное уравнение Вольтерра второго рода относительно неизвестной функции 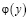 :
:
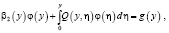 (10)
(10)
которое однозначно и безусловно разрешимо, где 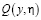 ,
, 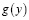 – известные достаточно гладкие функции.
– известные достаточно гладкие функции.
По найденному 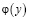 определяется
определяется 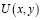 . Таким образом, решение задачи (1) – (4) существует, единственно, и определяется формулой (9).
. Таким образом, решение задачи (1) – (4) существует, единственно, и определяется формулой (9).
Пусть теперь 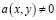 . Опираясь на свойства функции Грина для задачи (1) – (3) и
. Опираясь на свойства функции Грина для задачи (1) – (3) и 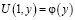 , будем иметь
, будем иметь
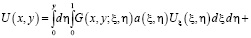
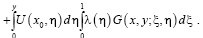 (11)
(11)
Из (11) интегрированием по частям, получим
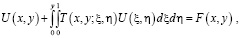 (12)
(12)
где 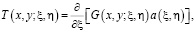
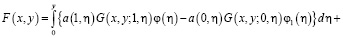
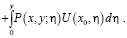
Обращая (12) через резольвенту 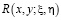 ядра
ядра 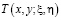 , будем иметь
, будем иметь
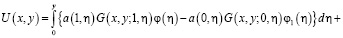
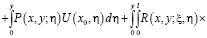
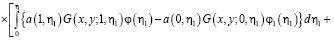
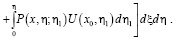 (13)
(13)
После преобразования (13), получим
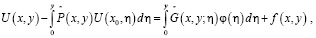 (14)
(14)
где 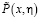 и
и 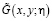 функции, свойства которых хорошо известны [7]. Полагая в (13)
функции, свойства которых хорошо известны [7]. Полагая в (13) 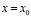 и считая правую часть известной, получим интегральное уравнение Вольтерра второго рода относительно
и считая правую часть известной, получим интегральное уравнение Вольтерра второго рода относительно 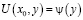 :
:
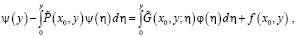
которое имеет единственное решение [11].
Найденное значение 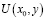 подставим в равенство (14). Удовлетворяя его граничному условию (4), снова получаем интегральное уравнение Вольтерра второго рода относительно
подставим в равенство (14). Удовлетворяя его граничному условию (4), снова получаем интегральное уравнение Вольтерра второго рода относительно 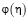 , которое однозначно разрешимо, т.к.
, которое однозначно разрешимо, т.к. 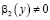 [7].
[7].
Отметим, что нелокальные задачи для уравнения смешанного типа исследовались также в работах [1-5, 8, 9, 12].



