Scientific journal

Advances in current natural sciences

ISSN 1681-7494

"Перечень" ВАК

ИФ РИНЦ = 0,775

В данной работе предпринята попытка разработать модель упрочнения малоуглеродистых сталей в результате взаимодействия дислокации с искусственно внедренными атомами азота в процессе многократной механико-термической обработки.

Известно несколько типов взаимодействии дислокации с примесными атомами (упругое, электрическое, химическое, геометрическое). В сплавах железа с азотом и углеродом в основном наблюдается упругое взаимодействие, т.е. когда в железе присутствуют дислокации, часть ее находится под напряжением сжатия, часть – под напряжением растяжения и часть – под сдвиговым напряжением. Упругие поля напряжений дислокации и примесного атома взаимодействуют и примесной атом азота испытывает со стороны дислокации силу притяжения.

Упругая энергия взаимодействия растворенного атома азота с дислокацией согласно Коттреллу равна 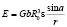[1]:

, (1)

где r и а – координаты внедренного атома азота в полярной системе координат с началом в центре дислокаций; b – вектор Бюргерса; G – модуль сдвига; e – фактор размерного несоответствия 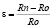; R_n – радиус примесного атома, R_o – радиус атома основы.

Концентрация атомов азота около дислокации можно определить из соотношения Максвелла-Больцмана:

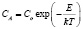, (2)

где C_o – средняя концентрация примеси в металле; Е – энергия взаимодействия атомов азота с дислокацией; k – константа Больцмана; Т – абсолютная температура.

Допускаем, что атомы азота насыщены вдоль линии дислокации, то в этом случае 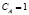и значение Е максимально.

Подставив в уравнение (2) значение 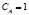, получим выражение для определения температуры насыщения азотом:

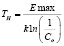. (3)

Расчеты по формуле (3) показывают, что атмосфера из атомов азота устойчивы до температур около 400 °С.

Необходимое количество атомов азота для образования насыщенных атмосфер зависит от плотности дислокации:

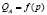, (4)

где р – плотность дислокаций, см2.

Данный параметр можно определить по формуле:

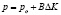, (5)

где р₀ – плотность дислокации в отожженном материале; В – коэффициент пропорциональности для малоуглеродистых сталей 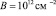; 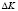– приращение пика Кестера, полученный экспериментальным путем

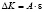, (6)

где А – коэффициент пропорциональности; 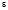– суммарная степень деформации.

Подставляя уравнение (6) в выражение (5) можно, определить плотность дислокации, в малоуглеродистой стали 10 в процессе насыщения азотом с последующей многократной механико-термической обработкой (НА+ММТО) и, следовательно, найти количество атомов азота, участвующие в блокировке дислокации, которые по расчетным данным, составляют от 0,95 до 3,91 % в зависимости от степени деформации [2].

При расчете упрочнения за счет искусственно внедренных атомов азота можно использовать в основном уравнение Орована [3]:

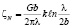(7)

где G – модуль сдвига; b – вектор Бюргерса; l – ближайшее расстояние между атомами; k – коэффициент, характеризующий тип взаимодействующих атомов с дислокацией.

Если в уравнение (7) ввести статический коэффициент 0,85, связывающий микроскопическое напряжение течения кристалла при произвольном расположении атомов азота с напряжением течения, определенным по среднему расстоянию между частицами, и подставить поправку в место l эффективную величину (l– l), т.е. расстояние между краями частиц, а не между их центрами, то уравнение Орована с учетом вышеприведенных уточнении имеет вид:

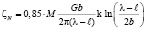. (8)

Здесь М – ориентационный множитель.

Анализ уравнения показывает, что в малоуглеродистых сталях параметры 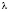и t характеризуют объемную долю атомов азота – VN

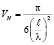(9)

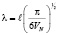(10)

Все остальные параметры в уравнении Орована (8) постоянны для данного сплава. Поэтому, применительно для малоуглеродистых сталей, уравнение Орована может быть выражено через численные коэффициенты: М = 2,75, G = 84000M7a, в = 0,25н.м, v = 0,33, К = 1,25 и параметры 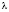, либо 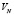и l. Тогда расчетное уравнение Орована для малоуглеродистых сталей примет вид:

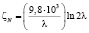(11)

Параметр l – расстояние между атомами азота можно определить экспериментально по данным электронной микроскопии тонких фольг.

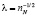, (12)

где n_N – число атомов азота на единицу площади.

Зная толщину фольги t и среднюю высоту частиц h, можно найти

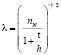(13)

ожидаемое среднеквадратичное отклонение измеренной величины Sλ

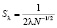, (14)

где N – число частиц, расположенных на снимках площадью Ғ Вариация величины

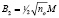, (15)

где n0 – число частиц в одном кадре, М – число кадров.

Таким образом, относительная погрешность определения обратно пропорционально корню квадратному из числа просчитанных частиц.

Упрочнение малоуглеродистых сталей зависит не только от упрочнения твердого раствора феррита атомами азота, но и от напряжения трения решетки – 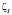, или напряжения Пайерлса – Набарро:

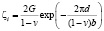, (16)

где G – модуль сдвига; d – межплоскостное расстояние; b – вектор Бюргерса.

Данное уравнение (16) можно рассчитать, если приближенно принять для малоуглеродистых сталей d b, v = 0,33

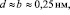v=0,33, G=84000 МПа

Механизм упрочнения малоуглеродистых сталей в процессе НА+ММТО так же зависит от упрочнения, обусловленного сопротивлением скользящей дислокаций с другими дислокациями в кристалле (дислокационное упрочнение).

Многократная пластическая деформация сопровождается образованием новых дислокаций, их взаимодействием друг с другом и увеличением их плотности. В этом случае упрочнение можно определить из следующего выражения (модель Тейлора):

, (17)

где а – коэффициент, зависящий от характера распределения и взаимодействия дислокации. Для малоуглеродистых сталей а = 0,20, М = 2,75; G = 84000 MПa; b = 0,25 нм, 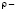плотность дислокации.

Плотность дислокации можно определить по формуле (5).

При многократной механико-термической обработке предварительно насыщенных атомами азота малоуглеродистых сталей образуется ячеистая дислокационная структура, которая будет влиять на механизм упрочнения сталей. Ячеистая дислокационная структура характеризуется высокой плотностью дислокаций в стенках ячейки. Согласно модели дальнодействующих напряжений (модель Кульман-Вильсдорф), стенки являются источниками дислокации. Вклад этих источников определяется длиной, т.е. средним расстоянием между узлами закрепления дислокации в стенках ячейки – L. В этом случае прочность стали будет связана с величиной, обратной L:

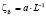. (18)

Далее, считая величину пропорциональной диаметру ячейки, получаем уравнение

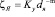, (19)

где Kу – коэффициент, характеризующий прочность блокирования дислокаций.

Для определения величины m уравнение (19) представляют графически в координатах 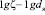, и по тангенсу угла наклона находят значение m. В ячеистой дислокационной структуре для ячеек любого размера m = 1. Следовательно, упрочнение металла в зависимости от ячеистой структуры имеет окончательный вид

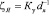. (20)

В целом механизм упрочнения малоуглеродистых сталей в процессе многократной механико-термической обработки предварительно насыщенных атомами азота состоит в совокупности из отдельных механизмов упрочнения.

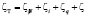. (21)

Таким образом, уравнение, описывающее механизм упрочнения малоуглеродистых сталей, имеет окончательный вид:

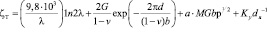. (22)

Результаты расчета по уравнению (22) представлены в таблице.

Показатели прочности малоуглеродистых сталей

Полученные результаты близки к экспериментальным данным.