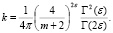Введение
Успехи современного естествознания требуют дальнейшего развития теории дифференциальных уравнений в частных производных, что приводит к необходимости исследования локальных и нелокальных задач для уравнений смешанного типа. К настоящему времени хорошо исследованы краевые задачи для уравнений смешанного типа, которые в гиперболической части области их задания редуцируются к уравнением Эйлера-Дарбу-Пуассона. Наряду с этим задачи со смещением и задачи типа задач Бицадзе-Самарского образуют широкий класс нелокальных задач, теория которых далека от окончательного завершения. Актуальность исследования таких задач можно обосновать как внутренними потребностями теоретического обобщения классических задач для уравнений математической физики, так и прикладными значениями.
Цель исследования: доказать однозначную разрешимость задачи Бицадзе- Самарского для уравнения смешанного типа в неограниченной области.
Постановка задачи. Рассматривается уравнение
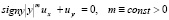(1)
в области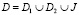 
плоскости комплексного переменного z = x + iy, где 
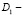полуплоскость 
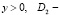конечная область полуплоскости 
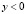, ограниченная характеристиками
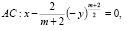
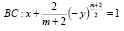
уравнения (1), выходящими из точек A(0,0), B(0,0) и отрезком AB прямой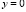 
; 
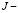интервал 
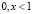прямой 
.
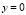Задача. Найти функцию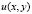 
со следующими свойствами:
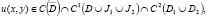причем
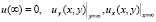
ограничены,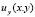 
при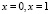 
может обращаться в бесконечность порядка 
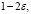где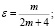 
2. 
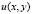удовлетворяет уравнению (1) в 
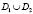и краевым условиям
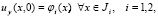(2)
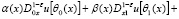
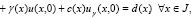(3)
где
,
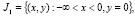
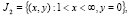
точки пересечения характеристик уравнения (1), выходящих из точки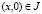 
с характеристиками AC и BC соответственно; 
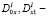операторы дробного в смысле Римана-Лиувилля интегро-дифференцирования [9]; φ(x), α(x), β(x), γ(x), c(x), d(x) – заданные функции, причем
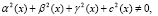
α(x), β(x), γ(x), c(x), d(x)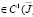 
);
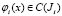и могут обращаться в бесконечность порядка не выше 
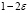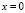при 
и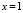 
, а при достаточно больших 
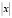удовлетворяют неравенству 
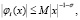где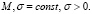 
Задача (1)-(3) относится к классу краевых задач со смещением [4], исследованием которых для уравнений смешанного типа занимались многие авторы [1,2,4-8]. Интерес к таким задачам обусловлен тем, что они существенно обобщают задачу Трикоми, содержат широкий класс корректных самосопряженных задач и имеют многомерные аналоги.
Теорема единственности. В области D не может существовать более одного решения задачи (1)-(3), если выполняются условия
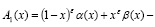
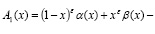(4)
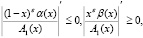
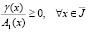(5)
где
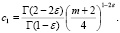
Доказательство. Пусть u(x,y) решение задачи, удовлетворяющей однородным граничным условиям
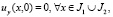
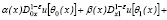
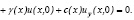
Очевидное тождество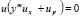 
перепишем в виде
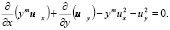
Проинтегрировав последнее по области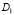 
и учитывая, что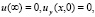 
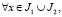получим
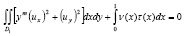, (6)
где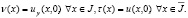 
Единственность решения задачи (1)-(3) будет следовать из (6), если мы докажем, что
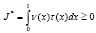
Выписывая решение задачи Коши в области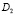 
[ 10] и удовлетворив условию (3), получим соотношение, между 
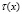и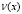 
, принесенное из области 
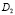на линию AB.
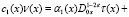
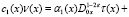(7)
где
)
)
)
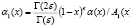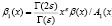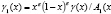При выполнении условий (4),(5) теоремы, пользуясь методикой, примененной в работах [5-8 ] , будем иметь
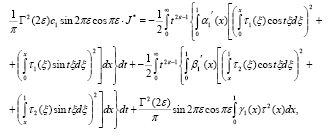
где
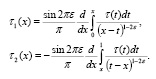
С учетом c1 sin2πε cosπε > 0 заключаем, что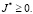 
Следовательно, решение задачи (1)-(2) единственно, так как 
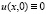в 
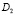как решение задачи Коши с нулевыми данными, а в 
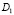как решение однородной задачи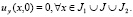 
Существования решения задачи.
Дополнительно будем предполагать, что
), 
),
).
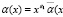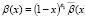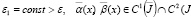Воспользуемся известным соотношением из области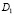 
(8)
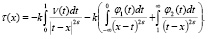
Исключив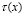 
из (7) и (8) вопрос существования решения задачи редуцируем к вопросу разрешимости сингулярного интегрального уравнения [3]
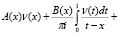
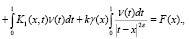(9)
где
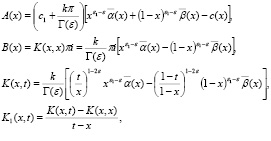
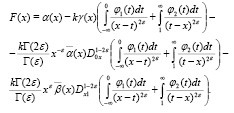
Здесь A(x) ≠ 0, A(x), B(x), γ(x) ∈ C1(J), правая часть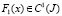 
и при 
и 
может обращаться в бесконечность порядка ниже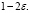 
Ядро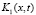 
имеет слабую особенность и допускает оценку
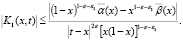
Действительно,
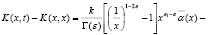
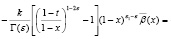
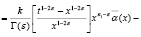
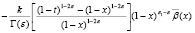
Так как
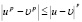
для любых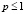 
и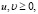 
то отсюда сразу следует наше утверждение.
Таким образом, задача (1)-(3) эквивалентна в смысле разрешимости сингулярному интегральному уравнению (9).
Условие
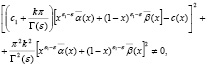
гарантирует существование регуляризатора, приводящего уравнение (9) к интегральному уравнению Фредгольма второго рода, безусловная разрешимость которого будет следовать из единственности решения задачи. По найденному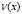 
можно определить 
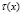и решение задачи (1)-(3) в области 
по формуле [10]
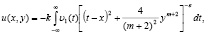
а в области D2 как решение задачи Коши [10]
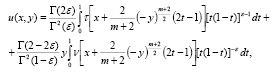
где
