Теория краевых задач для вырождающихся и смешанного типов уравнений в настоящее время является одним из важнейших разделов теории дифференциальных уравнений в частных производных и привлекает к себе внимание многих исследователей. За последние годы особенно интенсивно ведутся исследования задач со смещением и задач типа задачи Бицадзе – Самарского, что можно обосновать как внутренними потребностями обобщения классических задач для уравнений математической физики так и прикладным значением и связью с задачами газовой динамики, теории теплопроводности, теории упругости, теории плазмы, математической биологии и многими другими вопросами механики.
Для вырождающихся гиперболических и смешанного типов уравнений исследовались задачи, когда на характеристической части границы области задавалось нелокальное условие, поточечно связывающее значение решения или производная от него, вообще говоря, дробной определенного порядка, зависящего от порядка вырождения уравнения. Работ, посвященных исследованию случаев, когда в краевых условиях присутствуют дробные производные и интегралы произвольных порядков, не зависящих от порядка вырождения уравнения, сравнительно мало.
Цель исследования: Для вырождающегося гиперболического уравнения исследовать влияние порядков операторов дробного интегро-дифференцирования в краевом условии и коэффициента при младшей производной в уравнении на однозначную разрешимость задачи.
Постановка задачи. Рассмотрим уравнение
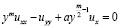, (1)
где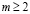 
, 
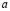
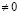– вещественная постоянная, в конечной области W, ограниченной характеристиками
,
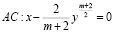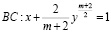
уравнения (1) и отрезком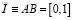 
прямой 
.
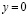Задача. Найти регулярное в области W решение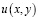 
уравнения (1) из класса 
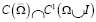, удовлетворяющее краевым условиям
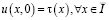(2)
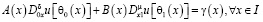, (3)
где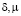 
– любые вещественные числа, 
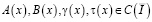, причем 
, 
, 
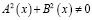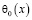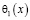– точки пересечения характеристик уравнения (1), выходящих из точки 
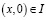с характеристиками AC, DC соответственно; 
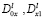– операторы дробного в смысле Римана-Лиувилля интегро-дифференцирования [5].
Задача (1) – (3) относится к классу краевых задач со смещением [4], исследованием которых для вырождающихся гиперболических и смешанного типов уравнений занимались многие авторы [1, 2, 4, 7–10].
Доказательство однозначной разрешимости задачи
При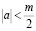 
решение задачи Коши для уравнения (1) имеет вид [6]
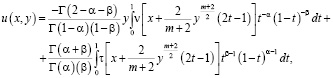(4)
а при 
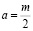
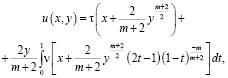(5)
где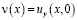 
; 
; 
; 
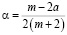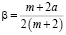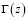– гамма функция Эйлера [3].
Удовлетворяя (4) краевому условию (3), получим интегральное уравнение относительно:
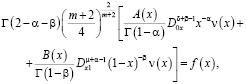(6)
где
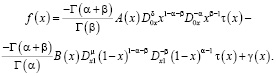
Теорема 1. Пусть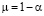 
, 
, 
, 
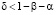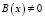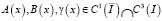. Тогда решение задачи (1) – (3) существует и единственно.
Действительно, при выполнении условий теоремы 1, уравнение (6) примет вид
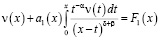, (7)
где
,
.
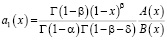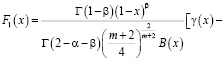
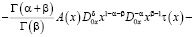
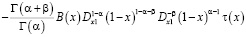Чтобы определить гладкость правой части уравнения (7) заметим, что [5]
,
,
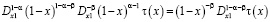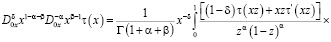
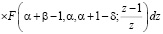где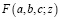 
– гипергеометрическая функция Гаусса [5].
Отсюда можно заключить, что
,
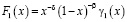где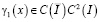 
– известная функция.
Пусть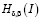 
класс функций 
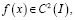могущих при 
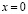обращаться в бесконечность порядка 
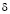, а при 
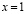в бесконечность порядка 
.
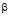Лемма. Пусть выполнены условия теоремы 1. Тогда уравнение (7) имеет единственное решение в классе функций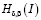 
.
Доказательство леммы проведено применением к уравнению (7) метода последовательных приближений [9].
По найденному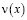 
и известному 
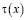решение задачи (1) – (3) определяется по формуле (4).
В случае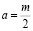 
, удовлетворяя (5) условию (3), вопрос существования решения задачи (1) – (3) эквивалентно редуцируется к разрешимости интегрального уравнения
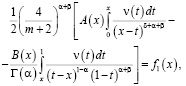(8)
где
.
Пусть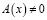 
. Подействовав на обе части (8) оператором 
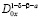, получим
,
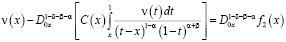где обозначено
, 
.
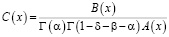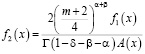Последнее уравнение в результате ряда преобразований сводится к уравнению Фредгольма второго рода относительно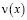 
со слабой особенностью в ядре
,
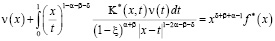где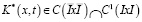 
, 
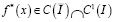– известные функции.
Теорема 2. Пусть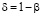 
, 
, 
, 
, 
, 
, 
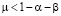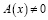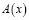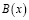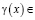
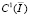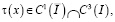тогда решение задачи (1) – (3) существует и единственно.
Доказательство, как и в случае теоремы 1, проводится путем редукции вопроса существования решения задачи (1)–(3) к разрешимости уравнения Вольтерра второго рода относительно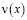 
со слабой особенностью в ядре и непрерывной правой частью.