Волокна определенных участков сердца можно рассматривать с электрической точки зрения как один эквивалентный коаксиальный проводник. Электрические параметры такого проводника определяются геометрией соответствующего участка проводящей системы сердца, физическими параметрами среды и величиной мембранного потенциала. Тогда для одномерной математической модели проводящую систему сердца можно представить как коаксиальный проводник с разветвлениями и различными электрическими параметрами на определенных участках. математическую модель такого процесса лучше всего описать как переходный процесс в цепи с распределенными параметрами. Применив для интегрирования дифференциального уравнения неявный метод формул дифференцировки назад, окончательно получаем математическую модель распространения сердечного потенциала действия

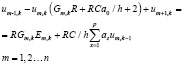
где G = G0Δx; R = R0Δx; C = C0Δx; а0, аS – коэффициенты метода ФДН; k – номер временного шага интегрирования; h – ширина временного шага интегрирования; p – порядок метода ФДН.

Порядок системы алгебраических уравнений определяется количеством линейных шагов интегрирования. Для решения этой системы на каждом временном шаге необходимо применение модифицированного метода Гаусса, с учетом особенностей ленточно-диагональной матрицы коэффициентов.

Разработанная математическая модель позволяет исследовать распространение возбуждения в сердце человека и может быть элементом для формирования сложных двумерных, а в перспективе и трехмерных моделей.