Развитие нелинейного мышления, устранение формализма в знаниях учащихся продолжают оставаться одними из важнейших целей обучения школьников математике, являясь проявлением методических направлений синергетического подхода в образовании [1, с. 284].
Общепризнано, что задачный материал является благоприятной почвой для реализации названного подхода. Среди задач, наиболее содействующих достижению вышеназванных целей, отметим задачи-альтернативы, задачи с неоднозначно понимаемым условием [2, с. 233; 3, с. 224], недостающими (неопределенные), избыточными (переопределенные), противоречивыми данными. Такие задачи способствуют расширению кругозора, адекватному применению знаний на практике, развитию мыслительных операций, логики рассуждений, критичности мышления, нестандартного подхода к решению проблем.
Учащиеся, как правило, игнорируют важные вопросы о переизбыточности, недостаточности или противоречивости задач, так как задачи из школьных учебников не требуют размышления над такими вопросами – в них обычно всегда имеется столько данных, сколько необходимо для решения. Этот факт является недостатком в математическом образовании школьников, так как не побуждает их к оценке условия задачи, а между тем задачи, возникающие из практики, как раз нуждаются в подобном анализе.
Остановимся на двух последних из перечисленных выше типов задач, т.е на задачах с избыточными (переопределенные) и противоречивыми данными.
1. В прямоугольнике стороны равны 8,4 см и 3,9 см, а периметр 24,6 см. Найти площадь прямоугольника.
Возможны различные варианты выделения лишнего данного в условии задачи. Избыточным данным можно считать одну из сторон прямоугольника или его периметр. Поскольку учащимся для вычисления площади прямоугольника нужны длины смежных сторон, а они даны в условии, то они объявляют периметр лишним данным, т. е. условие задачи избыточно. Учащиеся, как правило, удивляются на переопределенность задачи и только. Поэтому следует им предложить задачу, убеждающую их в том, что данные условия, кажущиеся лишними, помогают оценить корректность задачи.
2. В прямоугольнике длины сторон равны 6,7 см и 4,2 см, а площадь равна 25,3 кв. см. Требуется найти периметр прямоугольника.
Учащиеся делают вывод, что площадь – лишнее данное. Однако длины сторон в задаче не соответствуют периметру данного прямоугольника (т.е. с заданной площадью). Иначе говоря, формально «решив» задачу: (6,7 + 4,2)·2 = 21,8 (см), учащиеся нашли периметр не того прямоугольника, который дан, а прямоугольника с площадью 6,7·4,2 = 28,14 кв. см. Данная же задача решения не имеет в силу противоречивости условия, т. е. условие этой задачи не только избыточно, но и противоречиво.
Эта задача побуждает учащихся вернуться к предыдущей задаче и решить, является ли полученный формально ответ ее решением. Школьники приходят к положительному заключению, так как в ситуации первой задачи длины сторон соответствуют периметру: (8,4 + 3,9)·2 = 24,6, что, как они только что убедились, бывает не всегда и требует проверки.
3. Найти площадь треугольника со сторонами 10 см, 19 см и 8 см.
Учащиеся привыкли к тому, что им предлагаются всегда лишь корректные задачи, т.е. с однозначно трактуемым и «правильным» условием, допускающие вполне определенное (однозначное) решение. Поэтому, нисколько не сомневаясь, они используют формулу Герона, но под квадратным корнем получают отрицательное число. Это приводит их в тупик, но они и мысли не допускают, что здесь что-то не так в условии задачи, и перепроверяют свои вычисления. Редкий ученик обратится к критической оценке условия. Учителю приходится давать учащимся необходимую подсказку – воспользоваться неравенством треугольника, т.е. необходимым и достаточным условием (критерием) существования треугольника. Проверив условие при помощи неравенства треугольника, учащиеся убеждаются, что условие задачи противоречиво (8 < 19 – 10, т.е. одна из сторон треугольника меньше разности двух других сторон, а не больше!), откуда и следует вывод, что задача не имеет решения.
4. Найти площадь прямоугольного треугольника с катетами 9 см, 40 см и гипотенузой 42 см.
Учащиеся подходят формально к решению задачи: 9·40:2 = 180 (кв. см) и торопятся сообщить ответ учителю и классу. Каково же их удивление, когда учитель говорит, что их ответ неверен. Некоторые учащиеся по аналогии с предыдущей задачей начинают проверять корректность условия задачи с помощью неравенства треугольника, и поскольку оно выполняется для каждой из трех сторон, подтверждают ответ. Однако они забывают, что прямоугольный треугольник, кроме того, должен удовлетворять равенству теоремы Пифагора. Нередко учащимся в выборе критерия нужна помощь со стороны учителя, и обсуждение теоретической стороны этого вопроса весьма полезно для школьников. Треугольника с заданными длинами катетов и гипотенузы не существует: 92 + 402 ≠ 422, а потому неправомерно говорить о площади несуществующего объекта. Ответ здесь: задача не имеет решения, так как условие противоречиво. Без этого выяснения решение задачи не полно.
5. Найти площадь прямоугольника по стороне а, диагонали d и углу α между диагоналями.
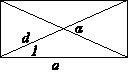
Геометрическое изображение условия задачи 5
Эта задача хороша тем, что имеет, по крайней мере, три различных способа решения. После совместного поиска и обсуждения путей решения задачи учитель может предложить разным группам учащихся (например, организовать работу по рядам) осуществить решение одним из рассмотренных способов.
1 способ, при котором сторона прямоугольника а становится лишним данным. Площадь прямоугольника находится как половина произведения диагоналей на синус угла между ними:
![]() кв. ед.
кв. ед.
2 способ, при котором угол α становится лишним данным, причем вторая сторона b находится по теореме Пифагора: b2 = d2 – а2, тогда площадь прямоугольника
![]() кв. ед.
кв. ед.
3 способ, при котором диагональ d – лишнее данное. В этом случае площадь прямоугольника ищется как произведение его смежных сторон:
![]() ,
,
поскольку ∠1 = ![]() . Итак,
. Итак,
![]() кв. ед.
кв. ед.
Далее следует установить, что все три выражения для площади прямоугольника равны. Например, преобразовать первые два выражения в выражение третьего вида:
![]()
![]() кв. ед.,
кв. ед.,
![]() кв. ед.
кв. ед.
Таким образом, одна задача с избыточным условием превратилась в три однозначно трактуемые задачи, причем данная задача – пример задачи именно с избыточным условием; в нем нет противоречий, благодаря чему задача имеет решение, и это решение единственно (хотя пути его нахождения, как мы видели, многообразны).
6. В параллелограмме стороны 3 см и 5 см, а высота 4 см. Найти площадь параллелограмма.
Учащиеся, как правило, уверенно проводят высоту к каждой из сторон параллелограмма и получают два разных ответа (12 см2 и 20 см2), т.е. рассматривают два случая, не задумываясь, возможны ли они. Между тем, высота длиной 4 см может быть опущена лишь на сторону параллелограмма длиной 3 см, так как в противном случае перпендикуляр к прямой оказывается длиннее наклонной, проведенной к этой же прямой из той же точки. Иначе говоря, при рассмотрении второго случая условие задачи становится противоречивым. Ответ один: 12 см2.
7. В параллелограмме стороны 4 см и 5 см, а высота 3 см. Найти площадь параллелограмма.
Если через некоторое время дается эта задача (а она похожа на предыдущую), то учащиеся, чаще всего, дают один ответ. Как говорится: обжегшись на молоке, дуют на воду. Между тем, в этой задаче оба случая возможны (это можно обосновать, и к этому надо приучать школьников). Ответ: 12 см2 или 15 см2.
8. Отрезок BD является биссектрисой ∆ АBC. Найдите DC, если AB = 30, AD = 20, BD = 16 и ∠BDC = ∠C.
На первый взгляд, эта задача не вызывает недоумений, и учащиеся ее решают, при этом реализуются разные пути решения. Одни учащиеся используют теорему о свойстве биссектрисы внутреннего угла треугольника (кстати, это самый короткий путь решения), другие используют свойства получающегося равнобедренного треугольника, теорему Пифагора, формулы площади треугольника (Герона и другие), теорему косинусов… И оказывается, что ответы не одинаковы. Это заставляет учащихся задуматься над возникшей проблемой. Высказывается сомнение о существовании такой конфигурации. Попытки построить полученную конфигурацию приводят к неудачам: либо DC не является продолжением AD, либо BD – не биссектриса. Тогда учащиеся делают правильный вывод: задача не имеет решения в силу противоречивости ее условия.
Заметим, что учащиеся могли и не заметить противоречия в задаче, если бы решили ее одним способом, что чаще всего и происходит в школе. В процессе работы с этой задачей школьники приобретают нестандартный опыт и делают вывод: не все, что легко разрешается, корректно. Подобные ситуации нередки в задачах, возникших из практических потребностей.
Из всего сказанного видно, что учащиеся не задумываются над вопросами об избыточности, недостаточности или противоречивости условий задач, не анализируют условие задачи, прежде чем начать её решение, не находят все возможные решения задач с неоднозначно понимаемым условием, не возвращаются с полученным результатом к началу задачи, чтобы проверить его. Работает стереотип: задача дана, значит, надо найти ее решение. Между тем, обоснованный вывод об отсутствии решения у задачи – это тоже решение, и понимание этого следует формировать у учащихся на протяжении всех лет обучения в школе.



