Scientific journal

Advances in current natural sciences

ISSN 1681-7494

"Перечень" ВАК

ИФ РИНЦ = 0,775

Концепция структурных уровней живых организмов позволяет расположить их в иерархическом соподчинении. Согласно критерию масштабности, биологический уровень включает подуровни: макромолекул (нуклеиновые кислоты, ДНК, РНК, белки), клеточный уровень, микроорганический (одноклеточные организмы), органов и тканей организмов в целом, популяционный, биоценозный и биосферный.

Живые организмы образуются из всевозможных малых органических молекул – мономеров, которые при объединении создают макромолекулы. Особую роль играют три класса мономеров: аминокислоты, нуклеотиды и моносахариды. Это те «кирпичики», из которых затем строятся полимерные макромолекулы – белки, нуклеиновые кислоты и полисахариды. Белки – это органические соединения, входящие в состав всех живых организмов, состоящие из большого числа мономеров. В состав белков входят 20 стандартных аминокислот. Свойства белков определяются пространственной трехмерной структурой их цепей. Изменяя в цепи лишь одну аминокислоту, можно получить молекулу с совершенно другой структурой и иными свойствами. Огромное разнообразие живых организмов на нашей планете определяется различиями в составе и пространственной форме составляющих их белков. Нуклеотиды – это мономерные звенья цепи нуклеиновых кислот. Они представляют собой химические соединения остатков трех веществ: азотистого основания, углевода и фосфорной кислоты. Существует два вида нуклеиновых кислот – дезоксирибонуклеиновая кислота (ДНК) и рибонуклеиновая кислота (РНК). ДНК содержит генетическую информацию о последовательности аминокислот в полипептидных цепях и определяет структуру белков. РНК отвечает за создание белков. Оказалось, что молекула ДНК состоит из двух мономерных цепей, идущих в противоположных направлениях и спирально закрученных одна вокруг другой. ДНК всего органического мира образованы соединением четырех видов нуклеотидов- аденин (A), гуанин (Г), цитозин (С) и тимин (Т), их расположение в молекуле ДНК дает указание молекуле РНК, как надо строить белок. Молекула РНК одноцепочная. Структура РНК также создается чередованием четырех типов нуклеотидов, но их состав несколько отличается от состава таковых в молекулах ДНК тем, что вместо тимина (Т) используется урацил (U) [1].

В биологических системах могут идти пpоцессы как с возpастанием, так и уменьшением энтpопии. Понятие энтропии имеет множество трактовок в самых разнообразных областях человеческих знаний. Наряду с энтропией Клаузиуса появилась статическая, информационная, математическая, лингвистическая, интеллектуальная и другие энтропии. Энтропия стала базисным понятием теории информации и стала выступать как мера неопределенности некоторой ситуации. Для характеристики меры сложности системы У. Эшби [11] впервые предложил использовать понятие энтропии. Система взаимодействует с внешним миром как единое целое. В целом же, система не теряет своей организованности или высокой упорядоченности. Открытые системы могут обмениваться с окружающими телами энергией, веществом и, что не менее важно, информацией. Чтобы биологическая система действовала и взаимодействовала со средой, она должна потреблять информацию из среды и сообщать информацию среде. Этот процесс называется информационным метаболизмом, который совместно с вещественным и материальным метаболизмом образует полный метаболизм. Впервые понятия энтропия и информация связал Шеннон [7]. С его подачи энтропия – это количество информации, приходящейся на одно элементарное сообщение источника, вырабатывающего статистически независимые сообщения. Получение какого-либо количества информации равно потерянной энтропии. Информационная энтропия для независимых случайных событий x с N возможными состояниями рассчитывается по формуле

,

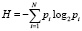где P_i – вероятность частоты встречаемости некоторого события.

Впервые для оценки степени структурированности биоценозов Мак-Артур в 1955 г. использовал общее уравнение энтропии Шеннона [12], в котором, pi заменил на pi = n_i /N; (где n_i – общее число особей вида i, N – общее число особей во всем биоценозе). В 1957 г. Р. Маргалеф постулировал теоретическую концепцию, согласно которой разнообразие соответствует энтропии при случайном выборе видов из сообщества [13]. В результате этих работ большое распространение и повсеместное признание получил индекс Шеннона Н, иногда называемый информационным индексом разнообразия К. Шеннона [3].

При расчете энтропии Н по Шеннону считается, что каждая проба – случайная выборка из сообщества, а соотношение видов в пробе отражает их реальное соотношение в природе. В качестве оценок вероятностей независимых событий рi для формулы (1) могут быть использованы следующие апостериорные отношения: удельная численность i-го вида, как частное от деления его численности ni на общую численность всех видов N, взятых для анализа (pi = n_i /N):

H = –Σn_i /N log₂ (n_i/N).

Использование индекса разнообразия Шеннона в экологии и, в частности, для оценки степени структурированности популяций и биоценозов очень детально обсуждается в работах [3, 8, 9]. Особенности функционирования биологических систем разного уровня с точки зрения теории информации были рассмотрены также в работе [10]. Шмальгаузеном были введены понятия о каналах прямой и обратной связи, по которым передается генетическая и фенотипическая информация, рассмотрены закономерности преобразования и кодирования биологической информации.

Целью данной работы является применение индекса Шеннона к биологическим системам, включающим подуровни: макромолекул (нуклеиновые кислоты, белки и РНК) и клеточный уровень.

В последние годы для комплексной оценки качества поверхностных вод сотрудниками кафедры экологической химии ЕГУ используется энтропийный индекс качества воды – G, который получается из индекса Шеннона [4]. G-функция характеризует гидроэкологические системы со стороны соотношения порядка и хаоса, мерами которых являются геоэкологическая синтропия – I [5] и энтропия Шеннона H, соответственно G = H/I. Значения G-функции говорят о том, что и в какой мере преобладает в структуре системы: хаос или порядок. Так, если G ˂ 1, то в структуре системы преобладает порядок, в противном случае, когда G ˃ 1, – хаос. При G = 1 хаос и порядок уравновешивают друг друга, и структурная организация системы является равновесной.

Методика расчета. Для расчета значений I, H и G пользуемся следующим вычислительным алгоритмом:

1. Определяется число элементов в системе – n.

2. Далее оценивается общая сумма элементов: N = ∑n.

3. Потом вычисляются: log₂N, nlog₂n и ∑ nlog₂n.

4. Рассчитывается геоэкологическая синтропия [11] (I) и энтропия (H):

I = ∑ nlog₂n / N и H = log₂N – I.

5. После чего определяется индекс качества воды: G = H/I.

В соответствии с целью работы и постановки задачи произведены расчеты функции белковых молекул, РНК, крахмала и живого тела.

Первичные структуры, белковые молекулы и РНК представляют собой, соответственно, последовательности аминокислотных остатков и нуклеотидов, и могут рассматриваться как системы, разделенные на части по одинаковым видам соответствующих аминокислот и нуклеотидов. Например, первичная структура молекулы глюкагона следующая:

His-Ser-Gln-Gly-Thr-Phe-Thr-Ser-Asp-Tyr-Ser-Lys-Tyr-Leu-Asp-Ser-Arg-Arg-Ala-Gln-Asp-Phe-Val-Gln-Trp-Leu-Met-Asn-Thr

Для глюкагона N = 29, число нуклеиновых кислот равно 15, а число одинаковых остатков (n) изменяется от 1 до 4. Соответствующие расчеты функций I, H и G приведены в табл. 1, откуда следует, что цепь глюкагона относится к хаотичному типу систем.

В табл. 2 даны значения I, H и G для белковых молекул.

Из табл. 1 и 2 видно, что аминокислотные цепи глукагона и кортикотропина обладают явной хаотичной структурой (G ˃ 1). Цепи же всех остальных белковых молекул относятся к синергетичному типу систем и проявляют тенденцию к уменьшению и приближению G = 1 по мере роста в белковой цепи общего числа аминокислотных остатков.

Приведем некоторые статистические данные по геному вируса HIVH3CG [6]. Расчеты приведены в табл. 3.

Так как для РНК G ˂ 0,2, то в структуре системы преобладает порядок.

В клетках живых систем найдены многие химические элементы, присутствующие в окружающей среде, однако необходимы для жизни лишь около 20 из них. Эти элементы получили название биогенных.

Таблица 1

Расчет значений I, H и G в структуре молекули глюкагона

Таблица 2

Значения N, I, H и G белковых молекул