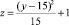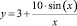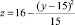Нечеткие переменные естественным образом возникают как исходные данные, для установления зависимостей между физико-геологическими параметрами, используемыми для прогноза одних физико-геологических параметров по другим [2, 3]. В отличие от традиционных методов вывода регрессионных уравнений по набору входных данных [1], и дальнейшего оперирования этими уравнениями как основой для прогноза параметров, концепция использования нечетких переменных основывается на полноценном учете всей совокупности данных, включая те неопределенности, которые реально существуют.
Основные концептуальные положения, лежащие в основе методов нечеткого моделирования, применительно к задачам моделирования в промысловой геологии состоят в следующем [4, 5]:
– влияние неоднородностей, присущих распределенным параметрам физико-геологической модели среды, проявляющимся в форме погрешностей измерений, приводит к нечеткости входных данных, используемых при моделировании, которые характеризуются распределением своих значений в выделенном диапазоне и ранжированным по уровню доверия результатам;
– те же факторы приводят к недоопределенности данных, используемых при построении зависимостей, с целью обучения прогнозу параметров по измеренным данным. Зависимости должны отражать объективную неопределенность связей между параметрами и быть ранжированными по достоверности во всем диапазоне своей области определения и допустимых значений;
– итоговая физико-геологическая модель, определенная как система распределенных геолого-геофизических параметров, должна наследовать ранжированную по достоверности неопределенность исходных данных в форме многовариантности и дифференцированной по компонентам вариантов оцененной достоверности.
Адекватным аппаратом, представления нечетких данных и нечетких зависимостей с оценкой их меры достоверности служат принципы нечеткого моделирования, основанного на трех компонентах:
– неопределенные данные с оценкой меры доверия представляются в форме функций принадлежности для нечетких величин;
– неопределенные связи с их дифференцированным ранжированием по достоверности представляются в форме отношений между нечеткими величинами;
– прогноз параметров модели с ранжированной оценкой достоверности реализуется построением функции принадлежности для пространственного распределения параметров физико-геологической модели и выполняется на принципах нечеткого логического вывода, основанного на функции принадлежности для измеренных нечетких величин и нечеткого отношения, между измеряемым и прогнозным параметрами полученными на этапе петрофизических исследований керна.
В приведенной концепции основными элементами служат:
Фазификация исходных данных – представление их в форме функций принадлежности ?(x, Ri) для исходных величин параметра x в локальных интервалах Ri, в которых будет выполняться прогнозирование.
Фазификация отношений, состоящая в построении функций принадлежности для отношений между исходными x, промежуточными y, h, …, ? и прогнозными параметрами z: ?(x, y), ?(y, h), ?(?, z).
Расчёт композиций нечётких отношений между входными параметрами для прогноза и итоговыми через систему промежуточных параметров y, h, …, ? для установления отношений ?(x, z) между начальными и конечными параметрами.
Для расчета функции принадлежности для параметра y по заданным на основе фазификации данных ??, функции принадлежности исходного параметра – ???(x), и установленной на основе фазификации данных ??, функции принадлежности для отношения между x и y – ???(x, y), используем традиционную максиминную нечёткую свёртку (композици
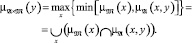 ):
):
(1)Эта формула соответствует обычному правилу матричной алгебры – произведение матрицы эквивалентной ???(x, y) на вектор ???(x), но сформулированному на языке логических умножений – пересечений и сумм – объедин
ений.Далее, по найденной ??????(y) и заданному отношению ??(y, z) н
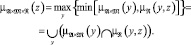 ходим
ходим
: (2)Подставляя выражение для ??????(y) в последнее соотношение,
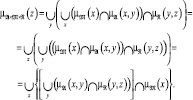 получ
получ
аем (3)
О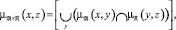 означ
означ
ив (4)получаем для ?
???????(z).Соотношение (4) переписывается содержательным раскрытием операций пересечения и объединения в эквивалентной форме следующ
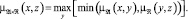 м обр
м обр
азом: (5)Это искомое соотношение для подстановок в представлениях функций принадлежности для нечетких величин. Соотношение (5) известно как композиция Мамдани ???(x, y) и ??(y, z) и, как выяснено, имеет смысл, аналогичный подстановке уравнений для исключения общих повторяющихся переменных. Этим обосновываются правила вычисления цепочек композиций промежуточных отношений для получения функции принадлежности итогового отношения ?????(x, z) между исходными и итоговыми прогнозными параметрами. Это исключительно важное и определяющее обстоятельство для формирования правил нечеткой математики, обеспечивающих анализ неопределенных нечетких данных, полученных в результате экспериментов. Оно обосновывает применимость композиции Мамдани отношений как подстановки нечетких зависимостей для нахождения итоговых законов, обеспечивающих прогноз нечетки
х параметров.Продемонстрируем эквивалентность этого правила обычным приемом подстановок уравнений в некоторых простей
ших случаях. Далее на рисунках приведены исходные данные и их нечеткие модели для отношений ???(x,
y) и ??(y, z).Для линейных
|
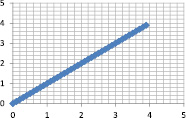
Исходные данные: y = x |
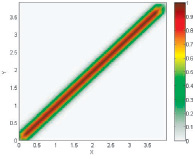
Нечеткая модель ???(x, y) |
|
|
|
|
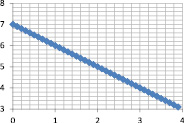
Исходные данные: z = 7 – y |
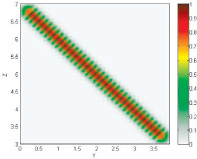
Нечеткая модель ??(y, z) |
|
|
|
а
в
исимостей:Композиция Мамдани ?????(x, z) этих отношений выглядит сле
д
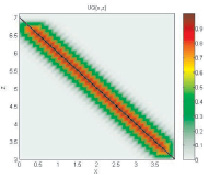 ю
ю
щим образом:Рис. 1. Композиция Мамдани линейных зависимостей: черным цветом обозначен график функций, полученный путем подста
новки уравненийКак видно, в полном соответствии с «алгебраической аналогией» происходит подстановка уравнений и исключение промежуточно
го параметра y.Для нелинейны
х
|
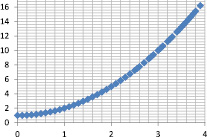
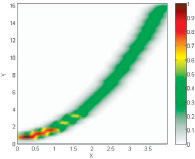
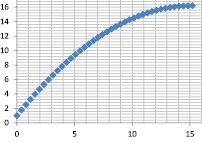
Исходные данные: y = x2 + 1 |
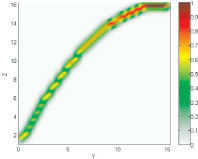
Нечеткая модель ???(x, y) |
|
|
|
|
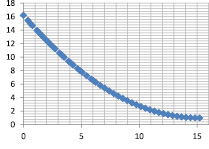
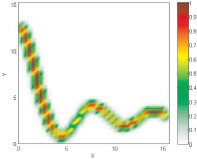
Исходные данные: |
Нечеткая модель ??(y, z) |
|
|
|
з
а
висимостей:Композиция Мамд
а
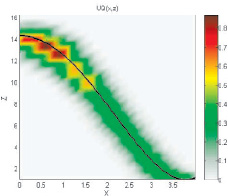 и
и
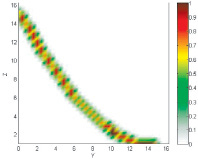
?????(x, z):Рис. 2. Композиция Мамдани нелинейных зависимостейДля более выраженных
|
Исходные данные: |
Нечеткая модель ???(x, y) |
|
|
|
|
Исходные данные: |
Нечеткая модель ??(y, z) |
|
|
|
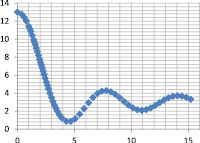
нелинейностей: Композиция Мамд

ни ?????(x, z):Рис. 3. Композиция Мамдани более выраженных нелинейных зависимостейПриведенные результаты позволяют использовать композицию Мамдани в моделях нечеткого анализа как нечеткий аналог подстановок зависимостей, что особо важно для установления отношений между величинами, характеризующими петрофизические и геофизические свойства горных пород.