В современный период климат претерпевает значительные изменения, об этом свидетельствуют результаты наблюдений за различными метеорологическими процессами в различных регионах планеты. Анализу временных рядов различной природы посвящено много работ [1, 3], а практическая реализация приведена в [2].
Поэтому исследование сезонных колебаний температуры, в различных климатических зонах, представляет не только практический, но и научный интерес.
В работе проводится анализ и исследование динамики температуры воздуха в Ставропольском крае (г. Ставрополь), по данным метеорологических наблюдений.
Результаты предварительного статистического анализа данных приведены ниже, в табл. 1.
Таблица 1
Описательная статистика
|
N |
Средн. |
Мин. |
Макс. |
Дисп. |
Стд. отк. |
Ст. ош. |
Асим. |
Эксц. |
|
|
Зима |
51 |
– 1,975 |
– 6,70 |
2,33 |
3,107 |
1,763 |
0,247 |
– 0,181 |
0,351 |
|
Весна |
51 |
8,907 |
6,33 |
10,97 |
1,256 |
1,121 |
0,157 |
– 0,167 |
– 0,753 |
|
Лето |
51 |
20,93 |
18,67 |
24,40 |
1,665 |
1,291 |
0,181 |
0,619 |
0,094 |
|
Осень |
51 |
9,917 |
5,633 |
12,63 |
1,753 |
1,324 |
0,185 |
– 0,550 |
0,967 |
Из данных таблицы следует, что наблюдается значительный размах температуры, особенно в зимний период, достигая более 9 градусов. Асимметрия отрицательна в зимний, весенний и осенний периоды и положительна в летний период. Эксцесс отрицателен весной и положителен в остальные сезоны. Значения асимметрии и эксцесса слабо-умеренные. Все это, в первую очередь, свидетельствует о наличии сложного тренда, и требуются более глубокие исследования для решения данной задачи.
Проведено также исследование тенденции изменения среднего значения температуры в современный период по сравнению с климатической нормой, с использованием критериев Крамера-Уэлча и Т-критерия Стьюдента. Результаты таких исследований приведены в табл. 2.
Таблица 2
T-критерий независимых выборок и критерий Крамера – Уэлча
|
Сред. 1 |
Сред. 2 |
t-знач. |
ст. св. |
p |
N1 |
N2. |
Ст. откл. |
Ст. откл. |
F-отн. |
p |
Крам-У |
|
|
Зима |
– 2,14 |
– 1,74 |
– 0,79 |
49 |
0,43 |
30 |
21 |
1,89 |
1,58 |
1,44 |
0,40 |
0,47 |
|
Весна |
8,83 |
9,02 |
– 0,60 |
49 |
0,55 |
30 |
21 |
1,25 |
0,92 |
1,84 |
0,16 |
0,55 |
|
Лето |
20,49 |
21,5 |
– 3,09 |
49 |
0,003 |
30 |
21 |
1,06 |
1,36 |
1,64 |
0,22 |
2,31 |
|
Осень |
9,749 |
10,2 |
– 1,09 |
49 |
0,283 |
30 |
21 |
1,18 |
1,51 |
1,63 |
0,22 |
0,74 |
Из данных таблицы следует, что зимой, весной и осенью рост температуры последних членов ряда незначительный, к тому же дисперсии в эти периоды значительны, достигая 3,1 – зимой, поэтому рост температуры может быть объяснен случайными факторами, а летом наблюдается тенденция роста температуры. Таким образом, среднее значение температуры в современный период больше климатической нормы (базовый период 1961–1990 гг.) только летом, как по Крамеру-Уэлчу (sig. = 2.317 > 1,96), так и по Т-тесту (sig. = 0,0033 < 0,05), на уровне значимости р = 0,05, в остальные сезоны года, хотя и наблюдается тенденция роста, она может быть объяснена случайностью изменений ряда.
Из предварительного анализа следует, что временной ряд температур в различные сезоны можно рассматривать как реализацию случайного процесса, состоящую из детерминированной и случайной части. Тогда, следуя методике [4, 5], для построения моделей динамики температур разлагаем временные ряды на основные составляющие: детерминированную и случайную части.
Так как ряды колеблющиеся, то необходимо детерминированную часть разложить на периодическую часть и полином невысокой степени, т.е. ряд можно описать полигармоническим процессом вида
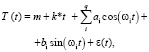 (1)
(1)
где ε(t) – случайная часть с нулевым математическим ожиданием.
Для выделения периодической составляющей используется известное и широко применяемое преобразование Фурье. При этом возникает две взаимосвязанные задачи:
– отделение случайной части от регулярной;
– выделение основных, так называемых, скрытых периодичностей.
Известно, что в разложении Фурье содержатся все гармоники и для выделения основных, необходимо использовать дополнительные критерии.
Сначала, как обычно, строим периодограммы и спектры рядов [1, 2], графики которых приведены на рис. 1 для летнего (слева) и осеннего (справа) сезонов.
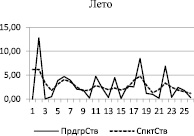
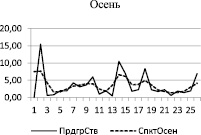
Рис. 1. Периодограммы (сплошная) и спектры (пунктирная) временных рядов
Из периодограмм видно, что они содержат много пиков, а спектры (построены с использованием спектрального окна Хемминга) – относительно небольшое число – 4–6 максимумов, в областях которых осуществляется поиск значимых гармоник.
В работе для отделения регулярной части от случайной используются следующие критерии случайности остатка ряда: Дарбина-Уотсона, числа поворотных точек, АКФ (автокорреляционная функция), коэффициенты корреляции Пирсона.
Как известно, для оценки степени корреляции остатка ряда используется статистика Дарбина-Уотсона, определяемая по формуле
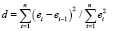 , (2)
, (2)
где ei – остаток ряда.
Составлены соответствующие программы на языке высокого уровня (Visual Basic), и проведены расчеты. Используя различные критерии случайности, проведен анализ остатка ряда, последовательно включая в циклический тренд пробные гармоники, полученные по результатам спектрального анализа.
Одним из критериев адекватности модели является невязка, определяемая по формуле
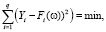 (3)
(3)
где Yi, Fi – фактические и модельные значения ряда, соответственно.
В качестве примера, результаты такого анализа, по данным наблюдений в предгорной зоне Ставропольского края (г. Ставрополь), для летней температуры, приведены в табл. 3.
Таблица 3
Значения критериев случайностей остатка ряда летнего сезона
|
Периоды (лет) |
Критерий Дарбина-Уотсона |
Число поворотных точек |
Невязка ( °С) |
Коэффициенты корр. Пирсона |
||||
|
Фкт-прогноз |
Дек-прогноз |
4253Н-прогноз |
||||||
|
Факт. |
Теор. |
Фак. |
Теор. |
|||||
|
50, 10, 5, 3,8, 2,9, 2,4 |
2,29 |
2 |
34 |
32,7 |
51,3 |
0,65 |
0,71 |
0,70 |
|
50, 10, 3,8 |
2,11 |
– |
32 |
– |
57,9 |
0,63 |
83 |
84 |
|
50, 5, 2,9 |
2,17 |
– |
32 |
– |
56,4 |
0,58 |
0,73 |
0,71 |
|
50, 10, 2,9 |
2,21 |
– |
28 |
– |
56,5 |
0,58 |
0,79 |
0,80 |
|
50, 5, 3,8 |
2,12 |
– |
36 |
– |
50,9 |
0,62 |
0,77 |
0,75 |
Данные таблицы показывают, что по комплексу параметров наиболее подходит вариант 2 (2 строка), так как по многим критериям, приведенным в таблице, он соответствует теоретическим значениям. Кроме того, вариант 2 лучше по значениям АКФ (рис. 2) и содержит период в области максимального значения на периодограмме.
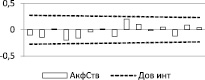
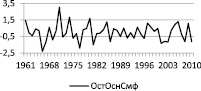
Рис. 2. АКФ остатков ряда (слева) и остатков ряда (справа)
На рис. 2 приведены некоторые результаты такого анализа.
Из графика (слева), следует, что АКФ остатка ряда, полученного как разность фактических и модельных значений выбранного варианта удовлетворяет условию случайности на уровне р = 0,05. По графику остатков ряда (справа) определяется число поворотных точек, теоретическое значение которого определяется по формуле [1]:
N = 2/3(n –2).
В предлагаемом методе для оценки степени адекватности построенной модели также проводится анализ регулярной части, используя коэффициенты корреляции Пирсона и результаты широко известных методов сглаживания временных рядов: метода классической декомпозиции и метода, основанного на использовании фильтра Ф4253Н [2].
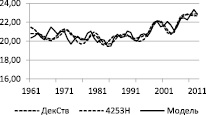
Рис. 3. Модельные значения (пунктирная) и результаты с использованием фильтра 4253Н (точечная) и метода декомпозиции (сплошная)
Эти методы позволяют более адекватно контролировать низкие гармоники, так как в случае коротких рядов в разложении ряда могут появиться «ложные» низкие гармоники, которые зависят к тому же от длины ряда. Такой комплексный анализ случайной и регулярной частей ряда, на наш взгляд, может позволить получить более адекватную модель. На рис. 3 приведены некоторые результаты такого анализа.
Из рисунка видно, что кривые, полученные по модели метода классической декомпозиции и метода с использованием фильтра 4253Н, хорошо согласуются, это также подтверждают коэффициенты корреляции Пирсона (см. табл. 2). При этом модельные значения более точно отображают особенности фактических значений ряда, тогда как методы с использованием фильтра и декомпозиции дают слишком сглаженные значения.
В результате такого комплексного анализа проводится окончательный выбор гармоник и построение моделей. Результаты полученных значений параметров моделей для всех сезонов года приведены в табл. 4.
Таблица 4
Параметры моделей температуры в различные сезоны года
|
Зима |
Весна |
|||||||||
|
Коэфф. лин. тр. |
Коэфф. Фурье |
Коэфф. лин. тр. |
Коэфф. Фурье |
|||||||
|
m |
k |
период |
кос |
син |
m |
k |
период |
кос |
син |
|
|
0,35 |
– 0,35 |
0,37 |
– 0,02 |
|||||||
|
– 2,3 |
0,012 |
25,4,2, 2,9 |
0,17 |
0,75 |
8,8 |
0,005 |
50, 5,6 , 2,9 |
0,58 |
0,34 |
|
|
– 0,27 |
– 0,35 |
– 0,09 |
0,03 |
|||||||
|
лето |
Осень |
|||||||||
|
0,74 |
0,06 |
0,86 |
0,05 |
|||||||
|
20,02 |
0,035 |
50, 10, 3,8 |
0,232 |
– 0,39 |
9,65 |
0,01 |
50, 5,6, 2,9 |
0,08 |
0,49 |
|
|
0,05 |
– 0,42 |
– 0,47 |
– 0,21 |
|||||||
Используя данные таблицы легко построить модели для всех сезонов, для этого достаточно из таблицы подставить в формулу (1) соответствующие коэффициенты Фурье и линейного тренда.
Так, например, для летнего сезона построена модель вида
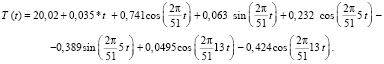
На рис. 4 приведены графики фактических и прогнозных значений температуры летнего сезона по построенной модели, до 2040 года.
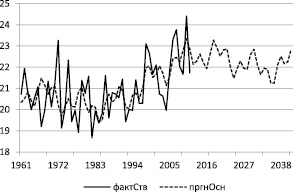
Рис. 4. Фактические (сплошная) и прогнозные (пунктирная) значения ряда
Из графиков рисунка следует, что в годы наблюдений кривые хорошо согласуются, что свидетельствует об адекватности построенной модели. Значения температуры изменяются достаточно сложным образом, совершая колебания около линейного тренда, указывающего на тенденцию роста. Максимальные значения она принимает в 2017–2022 и 2027–2030, а минимальные – в 2023–2026 и 2031–2037 годы.



