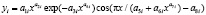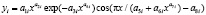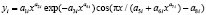Одним из возможных путей анализа дистанционного зондирования Земли является использование подходов математической морфологии ландшафтов – направления ландшафтоведения, изучающего количественные закономерности построения мозаик, образованных на земной поверхности, и разрабатывающего методы их математического анализа [1].
В статье [2] дан краткий обзор опыта применения гармонического анализа для морфометрической характеристики рельефа. Получены до 10 гармоник с постоянными периодом и амплитудой колебания. Преобразование Фурье может использоваться для задач классификации и районирования земной поверхности по ее гармоническим характеристикам, определяющим специфику топографического расчленения участка. В другой статье [3] показано, что цифровые модели рельефа и космические снимки позволяют выявить важные характеристики ландшафтов применительно к элементам рельефа, проследить изменения и спрогнозировать последствия природно-антропогенного и антропогенного воздействия на экосистемы.
По космическим снимкам получены координаты (широта, долгота, высота) по инструкции [4]. На линии стрежня в русле малой реки выбираются характерные точки по космическому снимку от истока до устья и составляется таблица исходных данных для последующего статистического моделирования методом идентификации волновых закономерностей [5].
Цель – выявление и анализ асимметричных вейвлетов по одной координате – приведенной к параметрам р. Ировка местной восточной долготе. Для этого от истока до устья в русле стрежня Ировки по кривизне русла выделили 290 характерных точек. Методика измерений была показана в статье [6].
Материалы и методы исследования
В табл. 1 даны измерения и их сравнение с моделями.
Таблица 1
Ранговые распределения характерных точек и местной долготы продольного профиля русла малой реки Ировка
|
Ранг точки |
Ранг Rβ |
Восточная долгота |
Долгота β, минута |
Расчетные значения |
||
|
β, минута |
ε18, минута |
Δ, % |
||||
|
0 |
20 |
E49 °20.09' |
17.39 |
17.425 |
0.0350129 |
0.20 |
|
1 |
19 |
E49 °20.20' |
17.50 |
17.527 |
0.0268094 |
0.15 |
|
2 |
17 |
E49 °20.32' |
17.62 |
17.611 |
–0.00942622 |
–0.05 |
|
3 |
15 |
E49 °20.37' |
17.67 |
17.609 |
–0.0605765 |
–0.34 |
|
… |
… |
… |
… |
… |
… |
… |
|
250 |
287 |
E49 °3.371' |
0.230 |
0.307 |
0.0767206 |
33.36 |
|
… |
… |
… |
… |
… |
… |
… |
|
287 |
171 |
E49 °4.719' |
2.019 |
2.010 |
–0.00857075 |
–0.42 |
|
288 |
164 |
E49 °4.735' |
2.035 |
2.048 |
0.0134797 |
0.66 |
|
289 |
172 |
E49 °4.717' |
2.017 |
2.032 |
0.0147019 |
0.73 |
Асимметричные вейвлет-сигналы записываются волновой формулой [5] вида
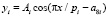 ,
,
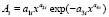 ,
,
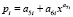 , (1)
, (1)
где y – учитываемый показатель (зависимый фактор), i – номер составляющей общей модели (1), m – количество членов в модели (1), x – объясняющая переменная (влияющий фактор), а1...а8 – параметры модели (1), принимающие числовые значения в ходе структурно-параметрической идентификации в программной среде CurveExpert-1.40, Ai – амплитуда (половина) вейвлета (ось y), pi – полупериод колебания (ось x).
Результаты исследования и их обсуждение
В табл. 2 приведены значения параметров модели (1) по 13 членам влияния местной широты на долготу.
Таблица 2
Влияние широты Север – Юг от истока до устья на долготу реки Ировка
|
Номер i |
Вейвлет |
Коэф. корр. r |
|||||||
|
Амплитуда (половина) колебания |
Полупериод колебания |
Сдвиг |
|||||||
|
a1i |
a2i |
a3i |
a4i |
a5i |
a6i |
a7i |
a8i |
||
|
1 |
19.08116 |
0 |
0.039811 |
1.32388 |
0 |
0 |
0 |
0 |
0.9976 |
|
2 |
–1.61185e–6 |
26.25390 |
14.89933 |
0.49461 |
0 |
0 |
0 |
0 |
|
|
3 |
–2.09089 |
0 |
0.82090 |
0.40884 |
2.36913 |
0.0028086 |
1.55183 |
–0.35993 |
|
|
Окончание табл. 2 |
|||||||||
|
Номер i |
Вейвлет |
Коэф. корр. r |
|||||||
|
Амплитуда (половина) колебания |
Полупериод колебания |
Сдвиг |
|||||||
|
a1i |
a2i |
a3i |
a4i |
a5i |
a6i |
a7i |
a8i |
||
|
4 |
1.95823e–5 |
0 |
0.448432 |
1.00282 |
0.0820466 |
0.0119878 |
1.00090 |
5.45636 |
0.4873 |
|
5 |
0.0168527 |
3.08551 |
0.378919 |
1.00055 |
1.58592 |
6.89209e–5 |
2.25901 |
2.74470 |
0.5584 |
|
6 |
4.51507e–6 |
4.65846 |
0.00126702 |
2.65421 |
0.156256 |
0.232502 |
0.219714 |
12.08418 |
0.3172 |
|
7 |
0.00742864 |
0 |
2.07429 |
0.127857 |
–0.0334208 |
1.99360 |
0.0795731 |
6.22674 |
0.3006 |
|
8 |
1.14486e–8 |
7.88750 |
0.253085 |
1.12234 |
5.64354 |
1.01837 |
0 |
0 |
0.2100 |
|
9 |
1.59713e–7 |
5.97718 |
0.379652 |
0.825954 |
0.857850 |
0 |
0 |
6.11295 |
0.2035 |
|
10 |
1.28249 |
0.788528 |
1.19686 |
0.595343 |
0.772734 |
0.0263791 |
0.913011 |
1.77834 |
0.3538 |
|
11 |
1.79254e–13 |
11.76514 |
0.564683 |
0.905328 |
0.375291 |
0 |
0 |
2.47176 |
0.1360 |
|
12 |
0.0264789 |
1.10650 |
0.119784 |
0 |
0.497133 |
0 |
0 |
1.05946 |
0.2198 |
|
13 |
1.31795e–8 |
11.27609 |
2.044278 |
0.735657 |
0.594690 |
0 |
0 |
0.978506 |
0.0465 |
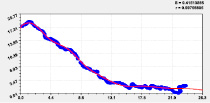
На рис. 1 даны графики трех членов и их объединения в одну формулу.
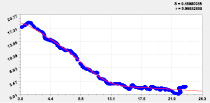
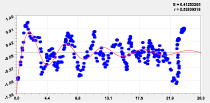
Двухчленный тренд Колебание
Двухчленный тренд и колебание Остатки после трехчленной модели
Рис. 1. Графики влияния широты Север – Юг от истока до устья на долготу от левой точки русла реки Ировка
Таким образом, распределение долготы от широты определяется волновыми уравнениями, причем они гораздо сложнее рядов Фурье, так как амплитуда и период колебаний переменные. Двухчленный тренд показывает, что малая река Ировка протекает в прямоугольнике 23.89 мин длиной (по местной широте Север – Юг) и 18.89 мин шириной (по местной долготе). Резкие изменения кривизны русла в плане по 290 характерным точкам дали 11 волновых уравнений (табл. 2). Таким образом, заметна фрактальность в строении рельефа и русла малой реки: чем точнее будут измерения ландшафта, тем больше будет выявлено вейвлетов.
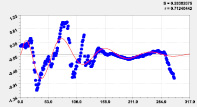
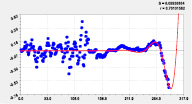
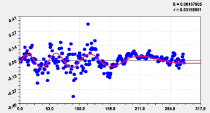
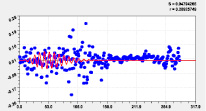
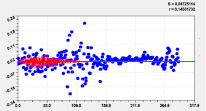
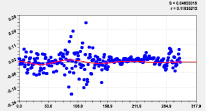
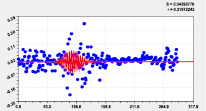
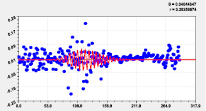
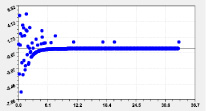
Идентификацией модели (1) было получено 18 вейвлетов долготы (табл. 3, рис. 2–4).
Таблица 3
Параметры (1) распределений по рангам долготы реки Ировка
|
Номер i |
Вейвлет |
Коэф. корр. r |
|||||||
|
Амплитуда (половина) колебания |
Полупериод колебания |
Сдвиг |
|||||||
|
a1i |
a2i |
a3i |
a4i |
a5i |
a6i |
a7i |
a8i |
||
|
1 |
18.74005 |
0 |
0.0018915 |
1.31141 |
0 |
0 |
0 |
0 |
0.9991 |
|
2 |
–3.54095e-14 |
94.91149 |
150.10476 |
0.21629 |
0 |
0 |
0 |
0 |
|
|
3 |
1.44702e6 |
6.58267 |
20.25179 |
0.17525 |
3.00095 |
30.03474 |
0.040801 |
0.14536 |
|
|
4 |
7.26081e-7 |
3.57383 |
0.00167623 |
1.62071 |
18.84378 |
8.39282e-5 |
1.89187 |
1.5461 |
0.7776 |
|
5 |
0.136962 |
0.711550 |
0.282787 |
0.558071 |
10.13446 |
0.0879591 |
0.572429 |
3.0931 |
0.5012 |
|
6 |
6.36221e-7 |
0 |
0.0411849 |
1.02605 |
04.72321 |
0.00560603 |
1.04115 |
0.592858 |
0.7010 |
|
7 |
0.00286152 |
1.02550 |
4.52966e-4 |
1.68641 |
6.85528 |
0.00267353 |
0.82799 |
1.68637 |
0.5040 |
|
8 |
1.02961e-27 |
15.84112 |
0.0635878 |
1.16178 |
1.94778 |
0 |
0 |
1.60019 |
0.2269 |
|
9 |
2.47538e-133 |
80.52037 |
0.6816976 |
0 |
4.99899 |
5.2465e-4 |
0.841448 |
1.59807 |
0.4686 |
|
10 |
0.0369682 |
0.184497 |
2.28544e-4 |
1.52781 |
23.39567 |
3.84322e-4 |
1.86656 |
1.77078 |
0.5315 |
|
11 |
5.86913e-4 |
1.55214 |
0.0254379 |
1.00020 |
8.72253 |
8.93225e-4 |
1.33455 |
1.58790 |
0.4655 |
|
12 |
9.29327e-5 |
2.05055 |
0.209654 |
0.613475 |
1.55638 |
0.00146157 |
1.55734 |
3.09580 |
0.3152 |
|
13 |
3.96597e-16 |
7.66169 |
0.0185167 |
1.17166 |
7.65696 |
0.00346936 |
1.21366 |
13.37270 |
0.1871 |
|
14 |
9.05519e-7 |
3.81736 |
0.0760401 |
1.00904 |
4.34034 |
332126e-4 |
1.13981 |
2.07944 |
0.2893 |
|
15 |
2.51056e-4 |
1.88212 |
0.0568959 |
0.994927 |
1.38098 |
2.34393e-4 |
1.04177 |
0.067522 |
0.1450 |
|
16 |
0.00716105 |
0.249398 |
5.24321e-4 |
1.52331 |
5.46810 |
0.966844 |
0 |
0 |
0.1184 |
|
17 |
4.58922e-63 |
37.51718 |
0.116845 |
1.21796 |
1.67233 |
0 |
0 |
2.19317 |
0.3101 |
|
18 |
6.0678e-34 |
19.30668 |
0.118273 |
1.05796 |
4.17660 |
0.00108311 |
1.22631 |
7.95796 |
0.3836 |
|
|
|
|
Двухчленный тренд |
Первое колебание |
|
|
|
|
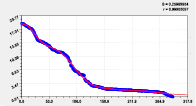
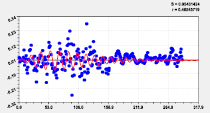
Двухчленный тренд и колебание |
Четвертая составляющая |
|
|
|
|
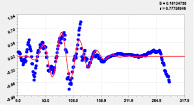
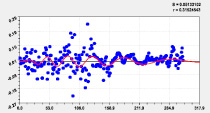
Пятая составляющая |
Шестая составляющая |
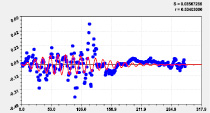
Рис. 2. Графики моделей распределения по рангам долготы реки Ировка
|
|
|
|
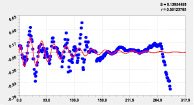
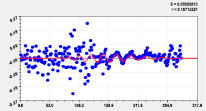
Седьмая составляющая |
Восьмая составляющая |
|
|
|
|
Девятая составляющая |
10-я составляющая |
|
|
|
|
11-я составляющая |
12-я составляющая |
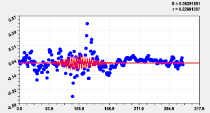
Рис. 3. Графики дополнительных моделей распределения долготы реки Ировка по рангам
|
|
|
|
13-я составляющая |
14-я составляющая |
|
|
|
|
15-я составляющая |
16-я составляющая |
|
|
|
|
17-я составляющая |
18-я составляющая |
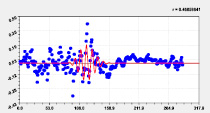
Рис. 4. Графики последних моделей распределения долготы реки Ировка по рангам
Первые три вейвлета дали коэффициента корреляции 0.9991. Первый член есть модифицированный закон Мандельброта [5], и он показывает экспоненциальный разворот русла на запад. Второй член по биотехническому закону [5] дает возбуждение рельефа на запад. Три колебания указывают на позитивное изменение ландшафта примерно до середины малой реки. А шестой член характерен для поведения устья малой реки Ировка.
Еще шесть членов показывают локальное изменение рельефа русла реки. Таким образом, географическая долгота вдоль русла малой реки изменяется, как и широта, волнообразно по асимметричным вейвлетам. На это влияет колеблющийся в плане стрежень русла малой реки Ировка между характерными точками малой реки.
На рис. 4 появляются вдоль реки несколько коротких вейвлетов.
После 18-го члена общей модели (1) процесс квантования вейвлетов сильно затрудняется. Это означает, что погрешность измерений дальше не позволяет получать высокую квантовую определенность. Для продолжения квантования всей речной системы нужно только уменьшить погрешность измерений. Рельеф получает квантовую запутанность только при значительном антропогенном влиянии. По-видимому, это замечательное математическое свойство стабильности динамики рельефа заключается в его естественной эволюции за очень продолжительное время (без влияния человека столетиями).
Остатки от 18-го колебания после рангового распределения долготы дали высокую погрешность моделирования 33.36 % ближе к устью на точке с рангом 250 (табл. 1). В этом месте происходит поворот малой реки Ировка на восток. По местной широте намного большая погрешность была получена в истоке Ировки (бесконечность), поэтому верховье реки летом пересыхает именно из-за изменений высоты в зависимости от широты и долготы.
По интервалам 0,1 погрешность распределилась так (по модулю): при нуле 3 шт. (1.03 %); 0–0,1 % всего 37 шт. (12,76 %); 0,1–0,2 % 29 шт. (10,00 %); 0,2–0,3 % 33 шт. (11,38 %); 0,3–0,4 % 24 шт. (8.28 %); 0,4–0,5 % 22 шт. (7,59 %) и т.д. По крупным интервалам: 0–1,0 % всего 203 шт. (70 %); от 0 до 5 % распределяются 277 характерных точек русла, что равна 95,52 % от 290 характерных точек. Норму погрешности измерений и моделирования примем 5 %, тогда оставшиеся 290 – 277 = 13 точек русла требуют отдельного рассмотрения.
|
|
|
|
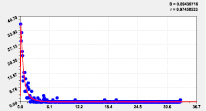
Двухчленный тренд |
Остатки после тренда |
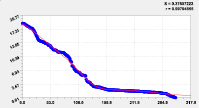
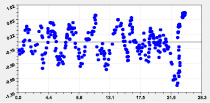
Рис. 5. Графики распределения погрешности моделирования долготы реки Ировка
На рис. 5 приведен график распределения погрешности модели по формуле
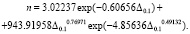 (2)
(2)
По остаткам от тренда (2) наибольший разброс наблюдается при погрешности моделирования до 5 %. По второй части этой формулы происходит резкий всплеск до 3 %.
Заключение
Моделирование распределений приведенной к данной местности малой реки долготы позволило получить 18 составляющих общей формулы вейвлета с распределением погрешности моделирования в основном до 5 %. При этом особое значение приобретает волновое изменение местной широты от Севера на Юг (было получено 25 членов) и местной долготы (19 членов рангового распределения) на примере от истока до устья малой реки Ировка). В итоге географические координаты малой реки в плане позволяют математически описать рельеф русла.
Первые три члена модели (1) для долготы дали адекватность по коэффициенту корреляции 0.9991. Уровень адекватности более 0.99, и он относится к сильнейшей факторной связи. Остальные 15 членов (1) увеличивают адекватность до 1. Долгота малой реки Ировка по космоснимкам позволяет получить высокую определенность процесса квантования вейвлетов.
По крупным интервалам погрешность моделирования после 18-го члена распределяется так: 0–1,0 % всего 203 шт. (70 %); от 0 до 5 % распределяются 277 характерных точек русла, что равно 95,52 % от 290 характерных точек. Норму погрешности измерений и моделирования примем 5 %, тогда оставшиеся 290 – 277 = 13 характерных точек русла малой реки Ировка требуют отдельного рассмотрения.